SAQ for Chapter 1 Real Numbers Class 10 Math NCERT
Important Questions1
An army contingent of 612 members is to march behind an army band of 48 members in a parade. The two groups are to march in the same number of columns. What is the maximum number of columns in which they can march?
Answer
Let the number of columns be x which is the largest number, which should divide both 612 and 48. It means x should be HCF of 612 and 48.We can write 612 and 48 as follows
612 = 2 × 2 × 3 × 3 × 5 × 17
48 = 2 × 2 × 2 × 2 × 3
HCF(612 × 28) = 2 × 2 × 3 = 12
Thus HCF of 104 and 96 is 12 i.e. 12 columns are required.
Here we have solved using Euclid’s algorithm but you can solve this problem by simple method of HCF.
SAQ's-II
2
Given that √5 is irrational, prove that 2√5 – 3 is an irrational number.
Answer
Assume that 2√5 – 3 is a rational number. Therefore, we can write it in the form of p/q where p and q are co–prime integers and q ≠ 0.Now 2√5 – 3 = p/q
Where q ≠ 0 and p and q are co–prime integers.
Rewriting the above expression as,
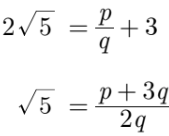
Here
is rational because p and q are co–prime integers, thus √5 should be a rational number. But √5 is irrational. This contradicts the given fact that √5 is irrational. Hence 2√5 – 3 is an irrational number.
SAQ's-II
3
Prove that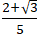 
is an irrational number, given that √3 is an irrational number.
is an irrational number, given that √3 is an irrational number. Answer
Assume that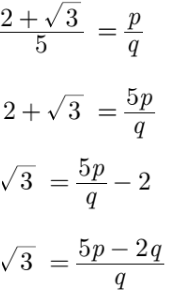 is a rational number. Therefore, we can write it in the form of p/q where p and q are co–prime integers and q ≠ 0. 
Since p and q are co–prime integers, then
is a rational number. But this contradicts the fact that √3 is an irrational number. So, our assumption is wrong. Therefore is an irrational number.
SAQ's-II
4
Given that √3 is irrational, prove that (5 + 2√3) is an irrational number.
Answer
Assume that (5 + 2√3) is a rational number. Therefore, we can write it in the form of p/q where p and q are co–prime integers and q ≠ 0.Now 5 + 2√3 = p/q
Where q ≠ 0 and p and q are integers.
Rewriting the above expression as,
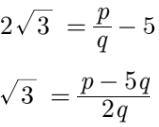
Here
is rational because p and q are co–prime integers, thus √3 should be a rational number. But √3 is irrational. This contradicts the given fact that √3 is irrational. Hence (5 + 2√3) is an irrational number.
SAQ's-II
5
Prove that 2 + 5√3 is an irrational number, given that √3 is an irrational number.
Answer
Assume that 2 + 5√3 is a rational number. Therefore, we can write it in the form of p/q where p and q are co–prime integers and q ≠ 0.2 + 5√3 = p/q, q ≠ 0
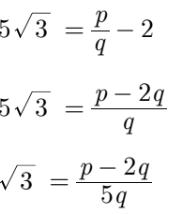
Here √3 is irrational and
is rational because p and q are co–prime integers. But rational number cannot be equal to an irrational number. Hence 2 + 5√3 is an irrational number.
SAQ's-II
6
Given that √2 is irrational, prove that (5 + 3√2) is an irrational number.
Answer
Assume that (5 + 3√2) is a rational number. Therefore, we can write it in the form of p/q where p and q are co–prime integers and q ≠ 0.Now 5 + 3√2 = p/q
where q ≠ 0 and p and q are integers.
Rewriting the above expression as,
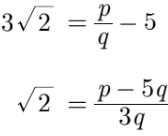
Here
is rational because p and q are co–prime integers, thus √2 should be a rational number. But √2 is irrational. This contradicts the given fact that √2 is irrational. Hence (5 + 3√2) is an irrational number.
SAQ's-II
7
Write the smallest number which is divisible by both 306 and 657.
Answer
The smallest number that is divisible by two numbers is obtained by finding the LCM of these number .Here, the given numbers are 306 and 657.
306 = 6 × 51 = 3 × 2 × 3 × 17
657 = 9 × 73 = 3 × 3 × 73
LCM(306, 657) = 2 × 3 × 3 × 17 × 73 = 22338
Hence, the smallest number which is divisible by 306 and 657 is 22338.
SAQ's-II
8
Show that numbers 8n can never end with digit 0 of any natural number n.
Answer
If the number 8n , for any n, were to end with the digit zero, then it would be divisible by 5 and 2. That is , the prime factorization of 8n would contain the prime 5 and 2. This is not possible because the only prime in the factorization of (8)n = (23)n = 23n is 2. The uniqueness of the Fundamental Theorem of Arithmetic guarantees that there are no other primes in the factorization of (8)n . Since there is no prime factor 5, (8)n cannot end with the digit zero.
SAQ's-II
9
144 cartons of Coke cans and 90 cartons of Pepsi cans are to be stacked in a canteen. If each stack is of the same height and if it equal contain cartoons of the same drink, what would be the greatest number of cartons each stack would have ?
Answer
The required answer will be HCF of 144 and 90.144 = 24 × 32
90 = 2 × 32 × 5
HCF(144, 90) = 2 × 32 = 18
Thus each stack would have 18 cartoons.
SAQ's-II
10
Three bells toll at intervals of 9, 12, 15 minutes respectively. If they start tolling together, after what time will they next toll together ?
Answer
The required answer is the LCM of 9, 12, and 15 minutes.Finding prime factor of given number we have,
9 = 3 × 3 = 32
12 = 2 × 2 × 3 = 22 × 3
15 = 3 × 5
LCM(9, 12, 15) = 22 × 32 × 5 = 150 minutes
The bells will toll next together after 180 minutes.
SAQ's-II
11
Find HCF and LCM of 16 and 36 by prime factorization and check your answer.
Answer
Finding prime factor of given number we have,
16 = 2 × 2 × 2 × 2 = 24
36 = 2 × 2 × 3 × 3 = 22 × 32
HCF(16, 36) = 2 × 2 = 4
LCM(16, 36) = 24 × 32
= 16 × 9 = 144
Check:
HCF(a, b) × LCM(a, b) = a × b
or, 4 × 144 = 16 × 36
576 = 576
Thus LHS = RHS
SAQ's-II
12
Find the HCF and LCM of 510 and 92 and verify that HCF × LCM = Product of two given numbers.
Answer
Finding prime factor of given number we have,92 = 22 × 23
510 = 30 × 17 = 2 × 3 × 5 × 17
HCF(510 × 92) = 2
LCM(510, 92) = 22 × 23 × 3 × 5 × 14 = 23460
HCF (510, 92) × LCM (510, 92)
= 2 × 23460 = 46920
Product of two numbers = 510 × 92 = 46920
Hence, HCF × LCM = Product of two numbers
SAQ's-II
13
The HCF of 65 and 117 is expressible in the form 65m – 117. Find the value of m. Also find the LCM of 65 and 117 using prime factorization method.
Answer
Finding prime factor of given number we have.117 = 13 × 2 × 3
65 = 13 × 5
HCF(117, 65) = 13
LCM(117, 65) = 13 × 5 × 3 × 3 = 585
HCF = 65m – 117
13 = 65m – 117
65m = 117 + 13 = 130
m = 130/65 = 2
SAQ's-II
14
Express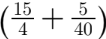 
as a decimal fraction without actual division.
as a decimal fraction without actual division. Answer
We have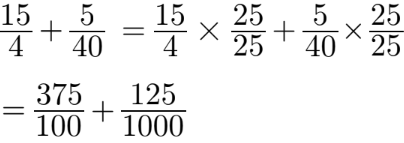
= 3.75 + 0.125 = 3.875
SAQ's-II
15
Express the number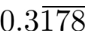 
in the form of rational number a/b .
in the form of rational number a/b . Answer
Let x = Imagex = 0.3178178178
10,000x = 3178.178178
10x = 3.178178…..
Subtracting , 9990x = 3175
or,
SAQ's-II
16
Prove that √2 is an irrational number.
Answer
Let √2 be a rational number.Then √2 = p/q,
where p and q are co – prime integers and q ≠ 0 On squaring both the sides we have,
or, p2 = 2p2
Since p2 is divisible by 2, thus p is also divisible by 2.
Let p = 2r for some positive integer r, then we have
p2 = 4r2
2q2 = 4r2
or, q2 = 2r2
Since q2 is divisible by 2, thus q is also divisible by 2.
We have seen that p and q are divisible by 2, which contradicts the fact that p and q are co–primes. Hence, our assumption is false and √2 is irrational.
SAQ's-II
17
If p is prime number, then prove that √p is an irrational.
Answer
Let p be a prime number and if possible, let √p be rationalThus √p = m/n ,
where m and n are co–primes and n ≠ 0.
Squaring on both sides, we get
or, pn2 = m2 …(1)
Here p divides pn2 . Thus p divides m2 and in result p also divides m.
Let m = pq for some integer q and putting m = pq in eq. (1), we have
pn2 = p2q2
or, n2 = pq2
Here p divides pq2. Thus p divides n2 and in result p also divides n.
[∵ p is prime and p divides n2 ⇒ p divides n]
Thus p is a common factor of m and n but this contradicts the fact that m and n are primes. The contradiction arises by assuming that √p is rational. Hence √p is irrational.
SAQ's-II
18
Prove that 3 + √5 is an irrational number.
Answer
Assume that that 3 + √5 is an irrational number, then we have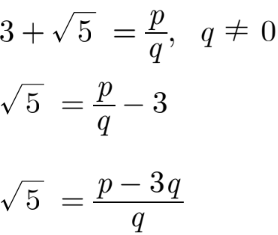
Here √5 is irrational and
is rational. But rational number cannot be equal to an irrational number. Hence 3 + √5 is an irrational number.
SAQ's-II
19
Prove that √5 is an irrational number and hence show that 2 – √5 is also an irrational number.
Answer
Assume that √5 be a rational number then we have√5 = a/b , (a, b are co – primes and b ≠ 0)
a = b√5
Squaring both the sides, we have
a2 = 5b2
Thus 5 is a factor of a2 and in result 5 is also a factor of a.
Let a = 5c where c is some integer, then we have
a2 = 25c2
Substituting a2 = 5b2 we have
5b2 = 25c2
b2 = 5c2
Thus 5 is a factor of b2 and in result 5 is also a factor of b.
Thus 5 is a common factor of a and b. But this contradicts the fact that a and b are co–primes. Thus, our assumption that √5 is rational number is wrong.
Hence √5 is irrational.
Let us assume that 2 – √5 be rational equal to a, then we have
2 – √5 = a
2 – a = √5
Since we have assume 2 – a is rational, but √5 is not rational. Rational number cannot be equal to an irrational number. Thus 2 – √5 is irrational.
SAQ's-II
20
Show that exactly one of the number n, n + 2 or n + 4 is divisible by 3.
Answer
If n is divisible by 3, clearly n + 2 and n + 4 is not divisible by 3.If n is not divisible by 3, then two case arise as given below.
Case 1: n = 3k + 1
n + 2 = 3k + 1 + 2 = 3k + 3 = 3(k + 1)
and n + 4 = 3k + 1 + 4 = 3k + 5 = 3(k + 1) + 2
We can clearly see that in this case n + 2 is divisible by 3 and n + 4 is not divisible by 3. Thus in this case only n + 2 is divisible by 3.
Hence, exactly one of the numbers n, n + 2, n + 4 is divisible by 3.
SAQ's-II