LAQ for Chapter 1 Real Numbers Class 10 Math NCERT

Answer

Assume that √3 is a rational number. Therefore, we can write it in the form of a/b where a and b are co – prime integers and q ≠ 0.
Assume that √3 be a rational number then we have
√3 = a/b ,
Where a and b are co – primes and b ≠ 0.
Now a = b√3
Squaring both the sides, we have
a² = 3b²
Thus 3 is a factor of a² and in result 3 is also a factor of a.
Let a = 3c where c is some integer, then we have a² = 9c²
Substituting a² = 3b² we have
3b² = 9c²
b² = 3c²
Thus 3 is a factor of b² and in result 3 is also a factor of b.
Thus 3 is a common factor of a and b. But this contradicts the fact that a and b are co – primes. Thus, our assumption that √3 is rational number is wrong.
Hence √3 is irrational.

Answer

Assume that √5 be a rational number then we have
√5 = a/b,
where a and b are co – primes and b ≠ 0.
a = b√5
Squaring both the sides, we have
a² = 5b²
Thus 5 is a factor of a² and in result 5 is also a factor of a.
Let a = 5c where c is some integer, then we have
a² = 25c²
Substituting a² = 5b² we have
5b² = 25c²
b² = 5c²
Thus 5 is a factor of b² and in result 5 is also a factor of b.
Thus 5 is a common factor of a and b. But this contradicts the fact that a and b are co – primes. Thus, our assumption that √5 is rational number is wrong.
Hence √5 is irrational.

Answer

Finding prime factor of given number we have,
378 = 2 × 3³ × 7
180 = 2² × 3² × 5
420 = 2² × 3 × 7 × 5
HCF(378, 180, 420) = 2 × 3 = 6
LCM (378, 180, 420) = 2² × 3³ × 5 × 7
= 2² × 3³ × 5 × 7 = 3780
HCF × LCM = 6 × 3780 = 22680
Product of given numbers
= 378 × 180 × 420
= 28576800
Hence, HCF × LCM ≠ Product of three numbers.

Answer

The fundamental theorem of arithmetic (FTA), also called the unique factorization theorem or the unique – prime – factorization theorem, states that every integer greater than 1 either is prime itself or is the product of a unique combination of prime numbers.
OR
Every composite number can be expressed as the product powers of primes and this factorization is unique.
Finding prime factor of given number we have,
2520 = 20 × 126 = 20 × 6 × 21
= 2³ × 3² × 5 × 7
10530 = 30 × 351 = 30 × 9 × 39
= 30 × 9 × 3 × 13
= 2 × 3⁴ × 5 × 13
LCM (2520, 10530) = 2³ × 3⁴ × 5 × 7 × 13
= 294840

Answer

If the number 6ⁿ for any n, were to end with the digit five, then it would be divisible by 5. That is, the prime factorization of 6ⁿ would contain the prime 5. This is not possible because the only prime in the factorization of 6ⁿ = (2 × 3)ⁿ are 2 and 3. The uniqueness of the Fundamental Theorem of Arithmetic guarantees that there are no other primes in the factorization of 6ⁿ . Since there is no prime factor 5, 6ⁿ cannot end with the digit five.

Answer

Fundamental theorem of Arithmetic: Every integer greater than one ither is prime itself or is the product of prime numbers and that this product is unique. Up to the order of the factors. LCM of two numbers should be exactly divisible by their HCF. In other words LCM is always a multiple of HCF. Since, 24 does not divide 540 two numbers cannot have their HCF as 24 and LCM as 540.
HCF = 24
LCM = 540

not an integer.

Answer

We have n³ – n = n(n² – 1)
= (n – 1) n(n + 1)
= (n – 1)n(n + 1)
Thus n³ – n is product of three consecutive positive integers.
Since, any positive integers a is of the form 3q, 3q + 1or 3q + 2 for some integer q.
Let a, a+ 1, a + 2 be any three consecutive integers.
Case I: a = 3q
If a = 3q then,
a(a + 1)(a + 2) = 3q(3q + 1)(3q + 2)
Product of two consecutive integers (3q + 1) and (3q + 2) is an even integer, say 2r.
Thus a(a + 1)(a + 2) = 3q(2r)
= 6qr, which is divisible by 6.
Case II: a = 3q + 1
If a = 3q + 1 then
a(a + 1)(a + 2)
= (3q + 1)(3q + 2)(3q + 3)
= (2r)(3)(q + 1)
= 6r(q + 1)
which is divisible by 6.
Case III: a = 3q + 2
If a = 3q + 2 then
a(a + 1)(a + 2)
= (3q + 2)(3q + 3)(3q + 4)
= 3(3q + 2)(q + 1)(3q + 4)
Here (3q + 2) and = 3(3q + 2)(q + 1)(3q + 4)
= multiple of 6 every q
= 6r (say)
which is divisible by 6. Hence, the product of three consecutive integers is divisible by 6 and n³ – n is also divisible by 3.

Answer

We have n² – n = n(n – 1)
Thus n² – n is product of two consecutive positive integers.
Any positive integer is of the form 2q or 2q + 1, for some integer q.
Case I: n = 2q
If n = 2q we have
n(n – 1) = 2q(2q – 1)
= 2m,
where m = q(2q – 1) which is divisible by 2.
Case II: n = 2q + 1
If n = 2q + 1, we have
n(n – 1) = (2q + 1)(2q + 1 – 1)
= 2q(2q + 1)
= 2m
where m = q(2q + 1) which is divisible by 2.
Hence, n² – n is divisible by 2 for every positive integer n.

Answer

Assume that √3 be a rational number then we have
√3 = a/b , (a, b are co-primes and b ≠ 0)
a = b√3
Squaring both the sides, we have
a² = 3b²
Thus 3 is a factor of a² and in result 3 is also a factor of a.
Let a = 3c where c is some integer, then we have a² = 9c²
Substituting a² = 9b² we have
3b² = 9c²
b² = 3c²
Thus 3 is a factor of b² and in result 3 is also a factor of b.
Thus 3 is a common factor of a and b. But this contradicts the fact that a and b are co – primes. Thus, our assumption that √3 is rational number is wrong.
Hence √3 is irrational.
Let us assume that 7 + 2√3 be rational equal to a, then we have
7 + 2√3 = p/q, q ≠ 0 and p and q are co-primes

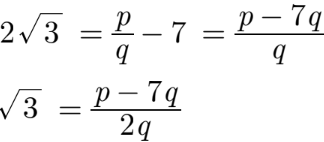
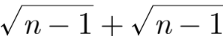Here p – 7q and 2q both are integers, hence √3 should be a rational number. But this contradicts the fact that √3 is an irrational number. Hence our assumption is not correct and 7 + 2√3 is irrational.

Answer

Let us assume that there is a positive integer n for which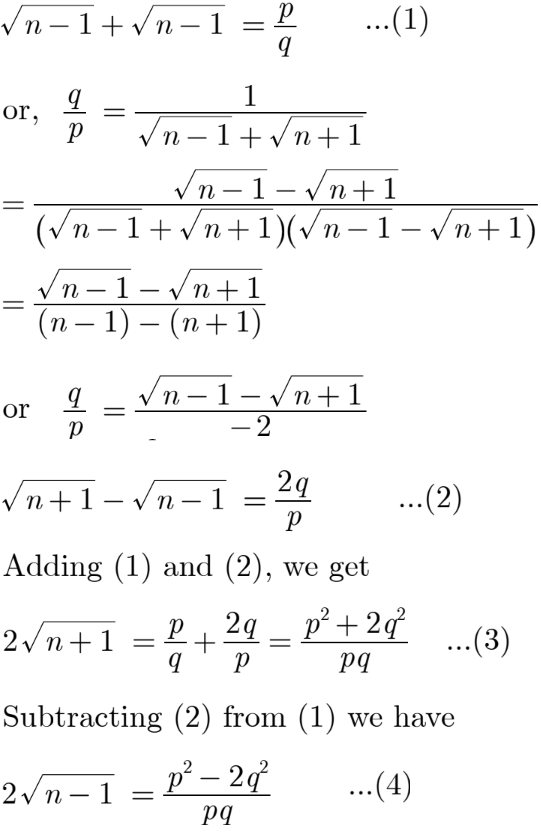  is rational and equal to p/q, where p and q are positive integers and (q ≠ 0).

From (3) and (4), we observe that  both are rational because p and q both are rational. But it possible only when (n + 1) and (n – 1) both are perfect squares. But they differ by 2 and two perfect squares never differ by 2. So both(n + 1) and (n – 1) cannot be perfect squares, hence there is no positive integer n for which  is rational.