SAQ for Chapter 1 Real Numbers Class 10 Math NCERT
Important Questions1
If HCF of 144 and 180 is expressed in the form 13m – 16. Find the value of m.
Answer
According to Euclid’s algorithm any number a can be written in the form,a = bq + r where 0 ≤ r < b
Applying Euclid’s division lemma on 144 and 180 we have
180 = 144 × 1 + 36
144 = 36 × 4 + 0
Here, remainder is 0 and divisor is 36. Thus HCF of 144 and 180 is 36.
Now 36 = 13m – 16
36 + 16 = 13m
52 = 13m ⇒ m = 4
SAQ's-I
2
Find HCF and LCM of 404 and 96 and verify that HCF × LCM = Product of the two given numbers.
Answer
We have404 = 2 × 2 × 101
= 22 × 101
96 = 2 × 2 × 2 × 2 × 2 × 3
= 25 × 3
HCF(404, 96) = 22 = 4
LCM(404, 96) = 101 × 25 × 3 = 9696
HCF × LCM = 4 × 9696 = 38784
Also, 404 × 96 = 38784
Hence, HCF × LCM = Product of 404 and 96
SAQ's-I
3
Find HCF of the numbers given below:
k, 2k, 3k, 4k and 5k, where k is a positive integer.
k, 2k, 3k, 4k and 5k, where k is a positive integer.
Answer
Here we can see easily that k is common factor between all and this is highest factor Thus HCF of k, 2k, 3k, 4k and 5k, is k.
SAQ's-I
4
Find the HCF and LCM of 90 and 144 by the method of prime factorization.
Answer
We have90 = 9 × 10 = 9 × 2 × 5
= 2 × 32 × 5
and 144 = 16 × 9
= 24 × 32
HCF = 2 × 32 = 18
LCM = 24 × 32 × 5 = 720
SAQ's-I
5
Given that HCF (306, 1314) = 18. Find LCM (306, 1314)
Answer
We have HCF (306, 1314) = 18LCM (306, 1314) = ?
Let a = 306 and b = 1314, then we have
LCM (a, b) × HCF(a, b) = a × b
Substituting values we have
LCM(a, b) × 18 = 306 × 1314
LCM(306, 1314) = 22,338
SAQ's-I
6
Complete the following factor tree and find the composite number x.
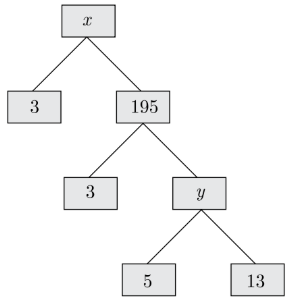

Answer
We have y = 5 × 13 = 65and x = 3 × 195 = 585
SAQ's-I
7
Explain why (7 × 13 × 11) + 11 and (7 × 6 × 5 × 4 × 3 × 2 × 1) + 3 are composite number.
Answer
(7 × 13 × 11) + 11 = 11 × (7 × 13 + 1)= 11 × (91 + 1)
= 11 × 92
and
(7 × 6 × 5 × 4 × 3 × 2 × 1) + 3
= 3(7 × 6 × 5 × 4 × 2 × 1 + 1)
= 3 ×(1681) = 3 × 41 × 41
Since given numbers have more than two prime factors, both number are composite.
SAQ's-I
8
Complete the following factor tree and find the composite number x .
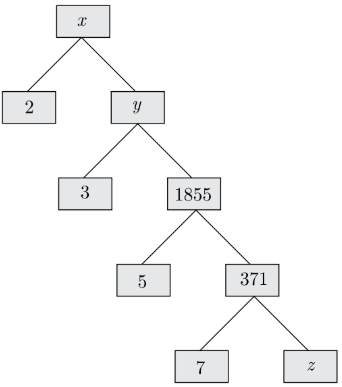

Answer
We havez = 371/7 = 53
y = 1855 × 3 = 5565
x = 2 × y = 2 × 5565 = 11130
Thus complete factor tree is as given below.

SAQ's-I
9
Find the missing numbers a, b, c and d in the given factor tree:
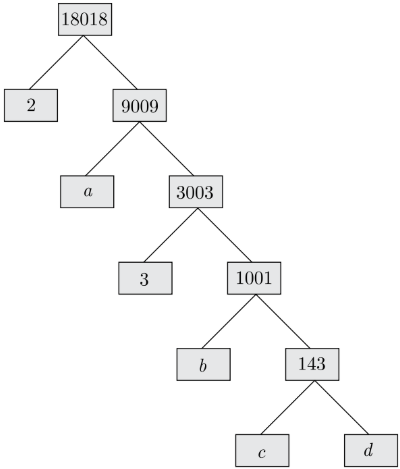

Answer
We have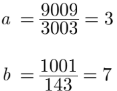
Since, 143 = 11 × 13,
Thus c = 11 and d = 13 or c = 13 and d = 11
SAQ's-I
10
Complete the following factor tree and find the composite number x.
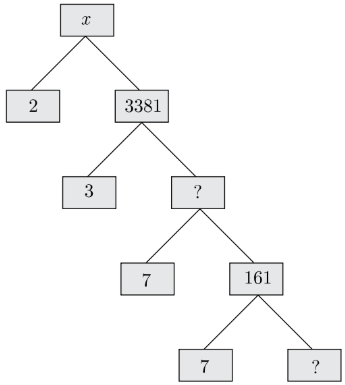

Answer
We complete the given factor tree writing variable y and z as following.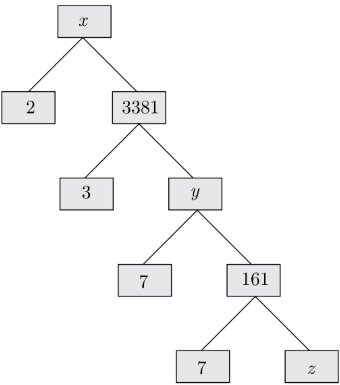
We have z = 161/7 = 23
y = 7 × 161 = 1127
Composite number, x = 2 × 3381 = 6762
SAQ's-I
11
Explain whether 3 × 12 × 101 + 4 is a prime number or a composite number.
Answer
A prime number (or a prime) is a natural number greater than 1 that cannot be formed by multiplying two smaller natural numbers. A natural number greater than 1 that is not prime is called a composite number. For example, 5 is prime because the only ways of writing it as a product, 1 × 5 or 5 × 1, involve 5 itself. However, 6 is composite because it is the product of two numbers (2 × 3) that are both smaller than 6. Every composite number can be written as the product of two or more (not necessarily distinct) primes.3 × 12 × 101 + 4 = 4(3 × 3 × 101 + 1)
= 4(909 + 1)
= 4(910)
= 2 × 2 × (10 × 7 + 13)
= 2 × 2 × 2 ×5 × 7 × 13
= a composite number
SAQ's-I
12
Complete the factor–tree and find the composite number M.
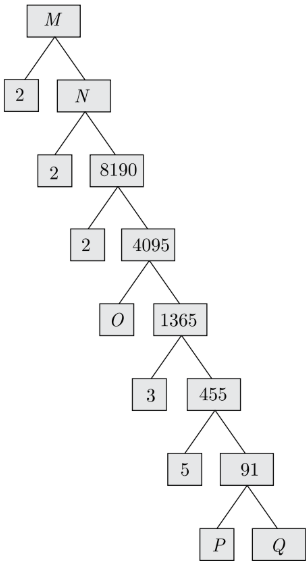

Answer
We have 91 = P × Q = 7 × 13So P = 7, Q = 13 or P = 13, Q = 7
O = 4095/1365 = 3
N = 2 × 8190 = 16380
Composite number,
M = 16380 × 2 = 32760
Thus complete factor tree is shown below.

SAQ's-I
13
Find the smallest natural number by which 1200 should be multiplied so that the square root of the product is a rational number.
Answer
We have 1200 = 12 × 100= 4 × 3 × 4 × 25
= 42 × 3 × 52
Here if we multiply by 3, then its square root will be 4 × 3 × 5 which is a rational number. Thus the required smallest natural number is 3.
SAQ's-I
14
Can two numbers have 15 as their HCF and their LCM? Give reasons.
Answer
LCM of two numbers should be exactly divisible by their HCF. Since, 15 does not divide 175, two numbers cannot have their HCF as 15 and LCM as 175.
SAQ's-I
15
15: Check whether 4n can end with the digit 0 for any natural number n.
Answer
If the number 4n, for any n, were to end with the digit zero, then it would be divisible by 5 and 2.That is, the prime factorization of 4n would contain the prime 5 and 2. This is not possible because the only prime in the factorization of 4n = 22n is 2. So, the uniqueness of the Fundamental Theorem of Arithmetic guarantees that there are no other primes in the factorization of 4n . So, there is no natural number n for which 4n ends with the digit zero. Hence 4n cannot end with the digit zero.
We have provided you with free PDF of this book which is far better than the books available in the market. You can do full study from this PDF but we request you to purchase hard copy of this book. Our mission is to make education easy and affordable to all through free digital educational resources. To full–fill this mission we require fund and we would like to raise that fund by selling hard copies of this book. Hard copy includes videos of each and every question. What will we do with that fund:
(a) We will provide PDF of all study material for free for all class.
(b) We will provide free access to all our videos on youtube.
(c) We will develop digital education resources so that there is no need for you to go to coaching institutes for JEE, NEET and other exam preparation.
Hard book includes QR code for each video and you can open video for every question by scanning of QR code in the book with your phone To purchase hard book click this link.
SAQ's-I
16
Show that 7n cannot end with the digit zero, for any natural number n.
Answer
If the number 7n , for any n, were to end with the digit zero, then it would be divisible by 5 and 2.That is, the prime factorization of 7n would contain the prime 5 and 2. This is not possible because the only prime in the factorization of 7n = (1 × 7)n is 7. So, the uniqueness of the Fundamental Theorem of Arithmetic guarantees that there are no other primes in the factorization of 7n . So, there is no natural number n for which 7n ends with the digit zero. Hence 7n cannot end with the digit zero.
SAQ's-I
17
Check whether (15)n can end with digit o for any n ∈ N.
Answer
If the number (15)n , for any n, were to end with the digit zero, then it would be divisible by 5 and 2.That is, the prime factorization of (15)n would contain the prime 5 and 2. This is not possible because the only prime in the factorization of (15)n = (3 × 5)n are 3 and 5. The uniqueness of the Fundamental Theorem of Arithmetic guarantees that there are no other primes in the factorization of (15)n . Since there is no prime factor 2, (15)n cannot end with the digit zero.
SAQ's-I
18
The length, breadth and height of a room are 8 m 50 cm, 6 m 25 cm and 4 m and 75 cm respectively. Find the length of the longest rod that can measure the dimensions of the room exactly.
Answer
Here we have to determine the HCF of all length which can measure all dimension.Length, l = 8 m 50 cm = 850cm
= 50 × 17 = 2 × 52 × 17
Breadth, b = 6 m 25 cm = 625 cm
= 25 × 25 = 52 × 52
Height, h = 4 m 75 cm = 475 cm
= 25 × 19 = 52 × 19
HCF(l, b, h) = HCF (850, 625, 475)
= HCF (2 × 52 × 17 , 52 , 52 × 19)
= 52 = 25 cm
Thus 25 cm rod can measure the dimensions of the room exactly. This is longest rod that can measure exactly.
SAQ's-I
19
Show that 5√6 is an irrational number.
Answer
Let 5√6 be a rational number, which can be expressed as a/b , where b ≠ 0; a and b are co–primes.Now 5√6 = a/b
√6 = a/5b
or, √6 = rational
But, √6 is an irrational number. Thus, our assumption is wrong. Hence, 5√6 is an irrational number.
SAQ's-I
20
Write the denominator of the rational number 257/500 in the form 2m × 5n , where m and n are non–negative integers. Hence write its decimal expansion without actual division.
Answer
We have 500 = 25 × 20= 52 × 5 × 4
= 53 × 22
Here denominator is 500 which can be written as 22 × 53 .
Now decimal expansion,
= 0.514
SAQ's-I