NCERT Solutions for Chapter 2 Polynomials Class 9 Maths
Book Solutions1
(i) 4x2 – 3x + 7
(ii) y2 + √2
(iii) 3√t+t√2
(iv) y+2/y
(v) x10 + y3 + t50
Answer
(i) 4x2 – 3x + 7
⇒ 4x2 – 3x + 7xo
∵ All the exponents of x are whole numbers.
∴ 4x2 – 3x + 7 is a polynomial in one variable.
(ii) y2 + √2
⇒ y2 + √2yo
∵ All the exponents of y are whole numbers.
∴ y2 + √2 is a polynomial in one variable.
(iii)3√t+t√2
⇒ 3t1/2 + √2.t
∵ 1/2 is not a whole number,
∴ 3t1/2 +√2.t ,
i.e. 3√t+ t√2 is not a polynomial.
(iv) y+ 2/y
If y + 2× y–1
∵ (–1) is not a whole number.
Y+2y−1 , i.e. y+ 2/y
∴ y+ 2/y is not a polynomial.
(v) x10 + y3 + t50
∵ Exponent of every variable is a whole number,
∴ x10 + y3 + t50 is a polynomial in x, y and t, i.e. in three variables.
2
(i) 2 + x2 + x
(ii) 2 – x2 + x3
(iii)
(iv) √2x-1
Answer
(i) 2 + x2 + x The co-efficient of x2 is 1.(ii) 2 – x2 + x3 The co-efficient of x2 is (–1).
(iv) √2x-1
∵ √2x −1 + 0∙X2
∴ The co-efficient of x2 is 0∙
3
Answer
(i) A binomial of degree 35 can be: 3x35 – 4(ii) A monomial of degree 100 can be: √2y100
4
(i) 5x3 + 4x2 + 7x
(ii) 4 – y2
(iii)5t − √7
(iv) 3
Answer
(i) 5x3 + 4x2 + 7x
∵ The highest exponent of x is 3.
∴ The degree of the polynomial is 3.
(ii) 4 – y2
∵ The highest exponent of y is 2.
∴ The degree of the polynomial is 2.
(iii) 5t − √7
∵ The highest exponent of t is 1.
∴ The degree of the polynomial is 1.
(iv) 3 since, 3 = 3x° [∵ x° = 1]
∴ The degree of the polynomial 3 is 0.
5
(i) x2 + x
(ii) x – x3
(iii) y + y2 + 4
(iv) 1 + x
(v) 3t
(vi) r2
(vii) 7x
Answer
(i) x2 + x ∵ The degree of x2 + x is 2.
∴ It is a quadratic polynomial.
(ii) x – x3
∵ The degree of x – x3 is 3.
∴ It is a cubic polynomial.
(iii) y + y2 + 4
∵ The degree of y + y2 + 4 is 2.
∴ It is a quadratic polynomial.
(iv) 1 + x
∵ The degree of 1 + x is 1.
∴ It is a linear polynomial.
(v) 3t
∵ The degree of 3t is 1.
∴ It is a linear polynomial.
(vi) r2
∵ The degree of r2 is 2.
∴ It is a quadratic polynomial.
(vii) 7x3
∵ The degree of 7x3 is 3.
∴ It is a cubic polynomial.
1
(i) x = 0
(ii) x = –1
(iii) x = 2
Answer
(i) ∵ p(x) = 5x – 4x2 + 3
= 5(x) – 4(x)2 + 3
∴ p(0) = 5(0) – 4(0) + 3
= 0 – 0 + 3 = 3
Thus, the value of 5x – 4x2 + 3 at x = 0 is 3.
(ii) ∵ p(x) = 5x – 4x2 + 3
= 5(x) – 4(x)2 + 3
∴ p(–1) = 5(–1) – 4(–1)2 + 3
= –5 – 4(1) + 3
= –5 – 4 + 3
= –9 + 3 = –6
∴ The value of 5x – 4x2 + 3 at x = –1 is –6.
(iii) ∵ p(x) = 5x – 4x2 + 3 = 5(x) – 4(x)2 + 3
∴ p(2) = 5(2) – 4(2)2 + 3
= 10 – 4(4) + 3
= 10 – 16 + 3 = –3
Thus the value of 5x – 4x2 + 3 at x = 2 is –3.
2
(i) p(y) = y2 – y + 1
(ii) p(t) = 2 + t + 2t2 – t3
(iii) p(x) = x3
(iv) p(x) = (x – 1) (x + 1)
Answer
(i) p(y) = y2 – y + 1
∵ p(y) = y2 – y + 1
= (y)2 – y + 1
∴ p(0) = (0)2 – (0) + 1
= 0 – 0 + 1 = 1
p(1) = (1)2 – (1) + 1
= 1 – 1 + 1 = 1
p(2) = (2)2 –2 + 1
= 4 – 2 + 1 = 3
(ii) p(t) = 2 + t + 2t2 – t3
∵ p(t) = 2 + t + 2t2 – t3
= 2 + t + 2(t)2 – (t)3
∴ p(0) = 2 + (0) + 2(0)2 – (0)3
= 2 + 0 + 0 – 0 = 2
p(1) = 2 + (1) + 2 (1)2 – (1)3
= 2 + 1 + 2 – 1 = 4
p(2) = 2 + 2 + 2(2)2 – (2)3
= 2 + 2 + 8 – 8 = 4
(iii) p(x) = x3 ∵ p(x)
= x3 = (x)3
∴ p(0) = (0)3
= 0 p(1) = (1)3 = 1
p(2) = (2)3
= 8 [∵ 2x2x2 = 8]
(iv) p(x) = (x – 1)(x + 1)
∵ p(x) = (x – 1)(x + 1)
∴ p(0) = (0 – 1)(0 + 1)
= –1 x 1 = –1
p(1) = (1 – 1)(1 + 1)
= (0)(2) = 0
p(2) = (2 – 1)(2 + 1)
= (1)(3) = 3
3
(ii) p(x) = 5x - π, x = 4/5
(iii) p(x) = x2 - 1, x = 1, -1
(iv) p(x) = (x + 1) (x - 2), x = -1, 2
(v) p(x) = x2 , x = 0
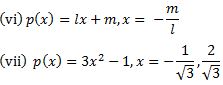
(viii) p(x) = 2x + 1, x = 1/2
Answer

(iii) Since, p(x) = x2 – 1
∴ p(1) = (1)2 – 1
= 1 – 1 = 0
Since, p(1) = 0,
∴ x = 1 is a zero of x2 – 1.
Also p(–1) = (–1)2 – 1
= 1 – 1 = 0
i.e. p(–1) = 0,
∴ x = –1 is also a zero of x2 – 1.
(iv) We have p(x) = (x + 1)(x – 2)
∴ p(–1) = (–1 + 1)(–1 – 2)
= (0)(–3) = 0
Since p(–1) = 0,
∴ x = –1 is a zero of (x + 1) (x – 1).
Also, p(2) = (2 + 1)(2 – 2)
= (3)(0) = 0
Since p(2) = 0,
∴ x = 2 is also a zero of (x + 1)(x – 1).
(v) We have p(x) = x2
∴ p(0) = (0)2 = 0
Since p(0) = 0,
∴ 0 is a zero of x2.
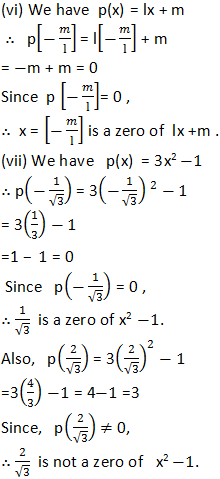
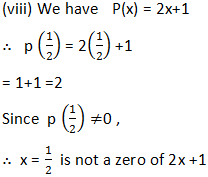
4(i)
p(x) = x + 5
Answer
We have p(x) = x + 5∴ p(x) = 0
⇒ x + 5 = 0
⇒ x = –5
Thus, a zero of x + 5 is (–5).
4(ii)
p(x) = x – 5
Answer
We have p(x) = x – 5∴ p(x) = 0
⇒ x – 5 = 0
⇒ x = 5
Thus, a zero of x – 5 is 5.
4(iii)
p(x) = 2x + 5
Answer
We have p(x) = 2x + 5∴ p(x) = 0
⇒ 2x + 5 = 0
⇒ 2x = –5
⇒ x = –5/2
Thus, a zero of 2x + 5 is –5/2
4(iv)
p(x) = 3x – 2
Answer
Since, p(x) = 3x – 2∴ p(x) = 0
⇒ 3x – 2 = 0
⇒ 3x = 2
⇒ x = 2/3
Thus, a zero of 3x – 2 is 2/3
4(v)
p(x) = 3x
Answer
Since, p(x) = 3x∴ p(x) = 0
⇒ 3x = 0
⇒ x = 0/3 = 0
Thus, a zero of 3x is 0.
4(vi)
p(x) = ax, a ≠ 0
Answer
Since, p(x) = ax, a ≠ 0⇒ p(x) = 0
⇒ ax = 0
⇒ x = 0 a = 0
Thus, a zero of ax is 0.
4(vii)
p(x) = cx + d, c ≠ 0, c, d are real numbers.
Answer
Since, p(x) = cx + d∴ p(x) = 0
⇒ cx + d = 0
⇒ cx = –d
⇒ x = – dc
Thus, a zero of cx + d is – dc.
1
(i) x + 1
(ii) x – 1/2
(iii) x
(iv) x + p
( v ) 5 + 2x
Answer
(i) ∵ The zero of x + 1 is –1 [∵ x + 1 = 0 ⇒ x = –1]
And by remainder theorem, when p(x) = x3 + 3x2 + 3x + 1 is divided by x + 1, then remainder is p(–1).
∴ p(–1) = (–1)3 + 3 (–1)2 + 3(–1) + 1
= –1 + (3 x 1) + (–3) + 1
= –1 + 3 – 3 + 1
= 0
Thus, the required remainder = 0
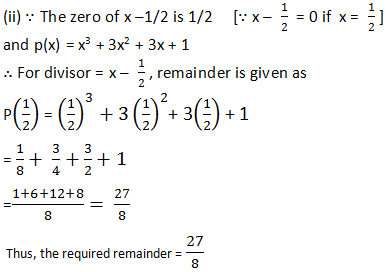
(iii) We have p(x) = x3 + 3x2 + 3x + 1 and the zero of x is 0
∴ p(0) = (0)3 + 3(0)2 + 3(0) + 1
= 0 + 0 + 0 + 1
= 1
Thus, the required remainder = 1.
(iv) We have p(x) = x3 + 3x2 + 3x + 1 and zero of x + p = (–π) [∵ x + π = 0 ⇒ x = – π]
∴ p(–π)= (– 5)3 + 3
(–π)2 + 3(–π) + 1
= –π3 + 3(π2) + (–3π) + 1
= –p3 + 3π2 – 3π + 1
Thus, the required remainder is –π + 3π2 – 3π + 1.
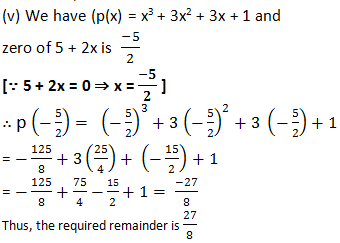
2
Answer
We have p(x) = x3 – ax2 + 6x – a∵ Zero of x – a is a. [∵ x – a = 0 ⇒ x = a]
∴ p(a) = (a)3 – a(a)2 + 6(a) – a
= a3 – a3 + 6a – a
= 0 + 5a
= 5a
Thus, the required remainder = 5a
3
Answer

1
(i) x3 + x2 + x + 1
(ii) x4 + x3 + x2 + x + 1
(iii) x4 + 3x3 + 3x2 + x + 1
(iv) x3 - x2 - (2 + √2)x + √2
Answer
For x + 1 = 0, we have x = –1.
∴ The zero of x + 1 is –1.
(i) p(x) = x3 + x2 + x + 1
∴ p(–1) = (–1)3 + (–1)2 + (–1) + 1
= –1 + 1 – 1 + 1 = 0
i.e. when p(x) is divided by (x + 1), then the remainder is zero.
∴ (x + 1) is a factor of x3 + x2 + x + 1.
(ii) ∵ p(x) = x4 + x3 + x2 + x + 1
∴ p(–1) = (–1)4 + (–1)3 + (–1)2 + (–1) + 1
= 1 – 1 + 1 – 1 + 1
= 3 – 2
= 1
∵ f(–1) ≠ 0
∴ p(x) is not divisible by x + 1. i.e. (x + 1) is not a factor of x4 + x3 + x2 + x + 1.
(iii) ∵ p(x) = x4 + 3x3 + 3x2 + x + 1
∴ p(–1) = (–1)4 + 3(–1)3 + 3(–1)2 + (–1) + 1
= (1) + 3(–1) + 3(1) + (–1) + 1
= 1 – 3 + 3 – 1 + 1
= 1 ≠ 0
∵ f(–1) ≠ 0
∴ (x + 1) is not a factor of x4 + 3x3 + 3x2 + x + 1.
(iv) ∵ p(x) = x3 – x2 – (2 + √2) x + √2)
∴ p(–1) = (–1)3 – (–1)2 – (2 + 2) (–1) + 2
= –1 – 1 – (–1) (2 + √2) + 2
= –1 – 1 + 1 (2 + √2) + 2
= –1 – 1 + 2 + √2 + √2)
= –2 + 2 + 2√2
= 2√2 ≠ 0
Since p(–1) ≠ 0.
∴ (x + 1) is not a factor of x4 + 3x3 + 3x2 + x + 1.
2(i)
p(x) = 2x3 + x2 - 2x - 1, g(x) = x + 1
Answer
We have p(x) = 2x3 + x2 – 2x – 1 and g(x) = x + 1∴ p(–1) = 2(–1)3 + (–1)2 – 2(–1) –1
= 2(–1) + 1 + 2 – 1
= –2 + 1 + 2 – 1
= –3 + 3 = 0
∵ p(–1) = 0
∴ g(x) is a factor of p(x).
2(ii)
p(x) = x3 + 3x2 + 3x + 1, g(x) = x + 2
Answer
We have p(x) = x3 + 3x2 + 3x + 1 and g(x) = x + 2∴ p(–2) = (–2)3 + 3(–2)2 + 3(–2) + 1
= –8 + 3(4) + (–6) + 1
= –8 + 12 – 6 + 1
= –8 – 6 + 12 + 1
= –14 + 13 = –1
∴ p(–2) ≠ 0
Thus, g(x) is not a factor of p(x).
2(iii)
p(x) = x3 - 4 x2 + x + 6, g(x) = x - 3
Answer
We have p(x) = x3 – 4x2 + x + 6 and g(x) = x – 3∴ p(3) = (3)3 – 4 (3)2 + (3) + 6
= 27 –4(9) + 3 + 6
= 27 – 36 + 3 + 6
= 0
Since g(x) = 0
∴ g(x) is a factor of p(x).
3(i)
p(x) = x2 + x + k
Answer
Here p(x) = x2 + x + kFor x – 1 be a factor of p(x), p(1) should be equal to 0.
We have p(1) = (1)2 + 1 + k
or p(1) = 1 + 1 + k
= k + 2
∴ k + 2 = 0
⇒ k= –2
3(ii)
p(x) = 2x2 + kx + √2
Answer
Here, p(x) = 2x2 + kx + √2For x – 1 be a factor of p(x), p(1) = 0
Since, p(1) = 2(1)2 + k(1) + √2
= 2 + k + √2
∵ p(1) must be equal to 0.
∴ k + 2 + √2 = 0
⇒ k = –2 – √2
or k = – (2 + √2).
3(iii)
p(x) = kx2 - √2x + 1
Answer
Here p(x) = kx2 – √2 x + 1 and g(x) = x – 1∴ For (x – 1) be a factor of p(x), p(1) should be equal to 0.
Since p(1) = k(1)2 – √2 (1) + 1
or p(1) = k – √2 + 1
or p(1) = k – √2 + 1
∴ k – √2 +1 = 0
⇒ k= √2 – 1
3(iv)
p(x) = kx2 - 3x + k
Answer
Here p(x) = kx2 – 3x + k and g(x) = x – 1For g(x) be a factor of p(x), p(1) should be equal to 0.
Since p(1) = k(1)2 – 3(1) + k
= k – 3 + k
= 2k – 3
∴ 2k – 3 = 0
⇒ k = 3/2
4
(i) 12x2 + 7x + 1
(ii) 2x2 + 7x + 3
(iii) 6x2 + 5x - 6
(iv) 3x2 - x - 4
Answer
(i) 12x2 – 7x + 1
Here co-efficient of x2 = 12
Co-efficient of x = –7 and constant term = 1
∴ a = 12, b = –7, c = 1
Now, l + m = –7 and
lm = ac = 12 x 1
∴ We have l = (–4) and m = (–3)
i.e. b = –7 = (–4 – 3).
Now, 12x2 – 7x + 1
= 12x2 – 4x – 3x + 1
= 4x(3x – 1) – 1(3x – 1)
= (3x – 1)(4x – 1)
Thus, 12x2 – 7x + 1 = (3x – 1)(4x – 1)
(ii) 2x2 + 7x + 3
Here, a = 2, b = 7 and c = 3
∴ l + m = 7 and lm = 2 x 3 = 6
i.e. 1 + 6 = 7 and 1 x 6 = 6
∴ l = 1 and m = 6
We have 2x2 + 7x + 3 = 2x2 + x + 6x + 3
= x(2x + 1) + 3(2x + 1)
= (2x + 1)(x + 3)
Thus, 2x2 + 7x + 3 = (2x + 1)(x + 3)
(iii) 6x2 + 5x – 6
We have a = 6, b = 5 and c = –6
∴ l + m = 5 and lm = ac = 6 x (–6) = –36
∴ l + m = 9 + (–4)
∴ 6x2 + 5x – 6
= 6x2 + 9x – 4x – 6
= 3x(2x + 3) – 2(2x + 3)
= (2x + 3)(3x – 2)
Thus, 6x2 + 5x – 6 = (2x + 3)(3x – 2)
(iv)3x2 – x – 4
We have a = 3, b = –1 and c = –4
∴ l + m = –1 and lm = 3 x (–4) = –12
∴ l = –4 and m = 3
Now, 3x2 – x – 4
= 3x2 – 4x + 3x – 4
= x(3x – 4) + 1(3x – 4)
= (3x – 4)(x + 1)
Thus, 3x2 – x – 4 = (3x – 4)(x + 1)
5(i)
x3 - 2x2 - x + 2
Answer
x3 – 2x2 – x + 2Rearranging the terms, we have x3 – 2x2 – x + 2
= x3 – x – 2x2 + 2
= x(x2 – 1) – 2(x2 – 1)
= (x2 – 1)(x – 2)
= [(x)2 – (1)2][x – 2]
= (x – 1)(x + 1)(x – 2) [∵ a2 – b2 = (a + b)(a – b)]
Thus, x3 – 2x2 – x + 2
= (x – 1)(x + 1)(x – 2)
5(ii)
x3 - 3x2 - 9x - 5
Answer
x3 – 3x2 – 9x – 5We have p(x) = x3 – 3x2 – 9x – 5
By trial,
let us find: p(1) = (1)3 – 3(1)2 – 9(1) – 5
= 3 – 3 – 9 – 5
= –14 ≠ 0
Now p(–1) = (–1)3 – 3(–1)2 – 9(–1) –5
= –1 – 3(1) + 9 – 5
= –1 – 3 + 9 – 5
= 0
∴ By factor theorem, [x – (–1)] is a factor of p(x).
∴ x2 – 3x2 – 9x – 5
= (x + 1)(x2 – 4x – 5)
= (x + 1)[x2 – 5x + x – 5] [Splitting –4 into –5 and +1]
= (x + 1) [x(x – 5) + 1(x – 5)]
= (x + 1) [(x – 5) (x + 1)]
= (x + 1)(x – 5)(x + 1)
5(iii)
x3 + 13x2 + 32x + 20
Answer
x3 + 13x2 + 32x + 20We have p(x) = x3 + 13x2 + 32x + 20
By trial,
let us find: p(1)=(1)3 + 13(1)2 + 32(1) + 20
= 1 + 13 + 32 + 20
= 66 ≠ 0
Now p(–1) = (–1)3 + 13(–1)2 + 32(–1) + 20
= –1 + 13 – 32 + 20
= 0
∴ By factor theorem, [x – (–1)],
i.e. (x + 1) is a factor p(x).
or x3 + 13x2 + 32x + 20
= (x + 1)(x2 + 12x + 20)
= (x + 1)[x2 + 2x + 10x + 20] [Splitting the middle term]
= (x + 1)[x(x + 2) + 10(x + 2)]
= (x + 1)[(x + 2)(x + 10)]
= (x + 1)(x + 2)(x + 10)
5(iv)
2y3 + y2 - 2y - 1
Answer
2y3 + y2 – 2y – 1We have p(y) = 2y3 + y2 – 2y – 1
By trial, we have p(1) = 2(1)3 + (1)2 – 2(1) – 1
= 2(1) + 1 – 2 – 1
= 2 + 1 – 2 – 1 = 0
∴ By factor theorem, (y – 1) is a factor of p(y).
∴ 2y3 – y2 – 2y – 1
= (y – 1)(2y2 + 3y + 1)
= (y – 1)[2y2 + 2y + y + 1] [Splitting the middle term]
= (y – 1)[2y(y + 1) + 1(y + 1)]
= (y – 1)[(y + 1)(2y + 1)]
= (y – 1)(y + 1)(2y + 1)
1(i)
(x + 4) (x + 10)
Answer
(x + 4)(x + 10):Using the identity (x + a)(x + b)
= x2 + (a + b)x + ab,
we have: (x + 4)(x + 10)
= x2 + (4 + 10)x + (4 x 10)
= x2 + 14x + 40
1(ii)
(x + 8) (x – 10)
Answer
(x + 8)(x – 10): Here, a = 8 and b = (–10)∴ Using (x + a)(x + b)
= x2 + (a + b)x + ab,
we have: (x + 8)(x – 10)
= x2 + [8 + (–10)]x + [8 x (–10)]
= x2 + [–2]x + [–80]
= x2 – 2x – 80
1(iii)
(3x + 4) (3x – 5)
Answer
(3x + 4)(3x – 5):
Using the identity (x + a)(x + b)
= x2 + (a + b)x + ab,
we have (3x + 4)(3x – 5)
= (3x)2 + [4 + (–5)]3x + [4 x (–5)]
= 9x2 + [–1]3x + [–20]
= 9x2 – 3x – 20
1(iv)
(y2 + 3/2) (y2 - 3/2)
Answer
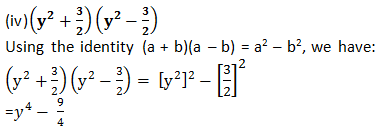
1(v)
(3 - 2x) (3 + 2x)
Answer
(3 – 2x)(3 + 2x):Using the identity (a + b)(a – b)
= a2 – b2,
we have: (3 – 2x)(3 + 2x)
= (3)2 – (2x)2
= 9 – 4x2
2(i)
103 × 107
Answer
We have 103 x 107= (100 + 3)(100 + 7)
= (100)2 + (3 + 7) x 100 + (3 x 7) [Using (x + a)(x + b) = x2 + (a + b)x + ab]
= 10000 + (10) x 100 + 21
= 10000 + 1000 + 21
= 11021
2(ii)
95 × 96
Answer
We have 95 x 96 = (100 – 5)(100 – 4)= (100)2 + [(–5) + (–4)] x 100 + [(–5) x (–4)] [Using (x + a)(x + b) = x2 + (a + b)x + ab]
= 10000 + [–9] x 100 + 20
= 10000 + (–900) + 20
= 9120
2(iii)
104 × 96
Answer
We have 104 x 96 = (100 + 4)(100 – 4)= (100)2 – (4)2 [Using (a + b)(a – b) = a2 – b2]
= 10000 – 16
= 9984
3(i)
9x2 + 6xy + y2
Answer
We have 9x2 + 6xy + y2= (3x)2 + 2(3x)(y) + (y)2
= (3x + y)2 [Using a2 + 2ab + b2 = (a + b)2]
= (3x + y)(3x + y)
3(ii)
4y2 - 4y + 1
Answer
We have 4y2 – 4y + 1
= (2y)2 – 2(2y)(1) + (1)2
= (2y – 1)2 [∵ a2 – 2ab + b2 = (a – b)2= (2y – 1)(2y – 1)]
3(iii)
x2 - y2/100
Answer
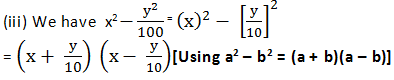
4(i)
(x + 2y + 4z)2
Answer
(x + 2y + 4z)2We have (x + y + z)2
= x2 + y2 + z2 + 2xy + 2yz + 2zx
∴ (x + 2y + 4z)2
= (x)2 + (2y)2 + (4z)2 + 2(x)(2y) + 2(2y)(4z) + 2(4z)(x)
= x2 + 4y2 + 16z2 + 4xy + 16yz + 8zx
4(ii)
(2x – y + z)2
Answer
(2x – y + z)2Using (x + y + z)2 = x2 + y2 + z2 + 2xy + 2yz + 2zx,
we have (2x – y + z)2
= (2x)2 + (–y)2 + (z)2 + 2(2x)(–y) + 2(–y)(z) + 2(z)(2x)
= 4x2 + y2 + z2 – 4xy – 2yz + 4zx
4(iii)
(–2x + 3y + 2z)2
Answer
(–2x + 3y + 2z)2Using (x + y + z)2 = x2 + y2 + z2 + 2xy + 2yz + 2zx,
we have (–2x + 3y + 2z)2
= (–2x)2 + (3y)2 + (2z)2 + 2(–2x)(3y) + 2(3y)(2z) + 2(2z)(–2x)
= 4x2 + 9y2 + 4z2 – 12xy + 12yz – 8zx
4(iv)
(3a – 7b – c)2
Answer
(3a – 7b – c)2Using (x + y + z)2 = x2 + y2 + z2 + 2xy + 2yz + 2zx,
we have (3a – 7b – c)2
= (3a)2 + (–7b)2 + (–c)2 + 2(3a)(–7b) + 2(–7b)(–c) + 2(–c)(3a)
= 9a2 + 49b2 + c2 + (–42ab) + (14bc) + (–6ca)
= 9a2 + 49b2 + c2 – 42ab + 14bc – 6ca
4(v)
(–2x + 5y – 3z)2
Answer
(–2x + 5y – 3z)2
Using (x + y + z)2 =x2 + y2 + z2 + 2xy + 2yz + 2zx,
We have (–2x + 5y – 3z)2
= (–2x)2 + (5y)2 + (–3z)2 + 2(–2x)(5y) + 2(5y)(–3z) + 2(–3z) (–2x)
=4x2 + 25y2 + 9z2 + [–20xy] + [–30yz] + [12zx]
=4x2 + 25y2 + 9z2 – 20xy – 30yz + 12zx
4(vi)
[1/4 a - 1/2 b + 1]2
Answer
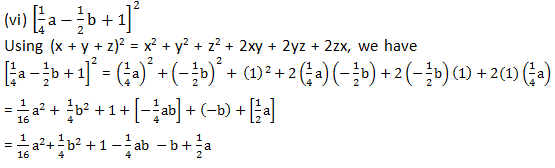
5(i)
4x2 + 9y2 + 16z2 + 12xy - 24yz - 16xz
Answer
4x2 + 9y2 + 16z2 + 12xy – 24yz – 16xz= (2x)2 + (3y)2 + (–4z)2 + 2(2x)(3y) + 2(3y)(–4z) + 2(–4z)(2x)
= (2x + 3y – 4z)2 [Using Identity V]
= (2x + 3y – 4z)(2x + 3y – 4z)
5(ii)
2x2 + y2 + 8z2 - 2√2 xy + 4√2 yz - 8xz
Answer
2x2 + y2 + 8z2 - 2√2 xy + 4√2 yz - 8xz= (-√2x)2 + (y)2 + (2√2z)2 + (2×-√2x×y) + (2×y×2√2z) + (2×2√2z×-√2x)
= (-√2x + y + 2√2z)2
= (-√2x + y + 2√2z) (-√2x + y + 2√2z)
6
(i) (2x + 1)3
(ii) (2a – 3b)3
(iii) [3/2 x + 1]3
(iv) [x - 2/3 y]3
Answer
Using Identity VI and Identity VII, we have
(x + y)3 = x3 + y3 + 3xy (x + y), and
(x – y)3 = x3 – y3 – 3xy (x – y).
(i) (2x + 1)3 = (2x)3 + (1)3 + 3(2x)(1)[(2x) + (1)]
= 8x3 + 1 + 6x[2x + 1] [Using Identity VI]
= 8x3 + 1 + 12x2 + 6x
= 8x3 + 12x2 + 6x + 1
(ii) (2a – 3b)3 = (2a)3 – (3b)3 – 3(2a)(3b)[(2a) – (3b)]
= 8a3 – 27b3 – 18ab (2a – 3b) [Using Identity VII]
= 8a3 – 27b3 – [36a2b – 54ab2]
= 8a3 – 27b3 – 36a2b + 54ab2
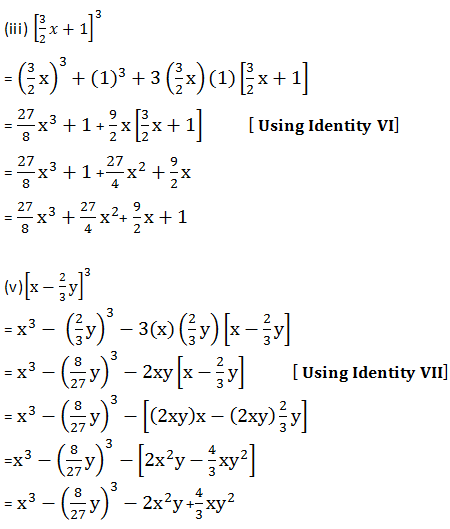
7(i)
(99)3
Answer
(99)3We have 99 = 100 – 1
∴ 993 = (100 – 1)3
= 1003 – 13 – 3(100)(1)(100 – 1)
= 1000000 – 1 – 300(100 – 1)
= 1000000 – 1 – 30000 + 300
= 1000300 – 30001
= 970299
7(ii)
(102)3
Answer
(102)3We have 102 = 100 + 2
∴ (102)3 = (100 + 2)3
= (100)3 + (2)3 + 3(100)(2) 100 + 2
= 1000000 + 8 + 600[100 + 2]
= 1000000 + 8 + 60000 + 1200
= 1061208
7(iii)
(998)3
Answer
(998)3We have 998 = 1000 – 2
∴ (999)3 = (1000 – 2)3
= (1000)3 – (2)3 – 3(1000)(2)[1000 – 2]
= 1000000000 – 8 – 6000[1000 – 2]
= 1000000000 – 8 – 6000000 – 12000
= 994011992
8(i)
8a3 + b3 + 12a2b + 6ab2
Answer
8a3 + b3 + 12a2b + 6ab2= (2a)3 + (b)3 + 6ab(2a + b)
= (2a)3 + (b)3 + 3(2a)(b)(2a + b)
= (2a + b)3 [Using Identity VI]
= (2a + b)(2a + b)(2a + b)
8(ii)
8a3 - b3 - 12a2b + 6ab2
Answer
8a3 – b3 – 12a2b + 6ab2= (2a)3 – (b)3 – 3(2a)(b)(2a – b)
= (2a – b)3 [Using Identity VII]
= (2a – b)(2a – b)(2a – b)
8(iii)
27 - 125a3 - 135a + 225a2
Answer
27 – 125a3 – 135a + 225a2= (3)3 – (5a)3 – 3(3)(5a)[3 – 5a]
= (3 – 5a)3 [Using Identity VII]
= (3 – 5a)(3 – 5a)(3 – 5a)
8(iv)
64a3 - 27b3 - 144a2b + 108ab2
Answer
64a3 – 27b3 – 144 a2b + 108 ab2= (4a)3 – (3b)3 – 3(4a)(3b)[4a – 3b]
= (4a – 3b)3 [Using Identity VII]
= (4a – 3b)(4a – 3b)(4a – 3b)
8(v)
27p3 - 1/216 - 9/2 p2 + 1/4 p
Answer
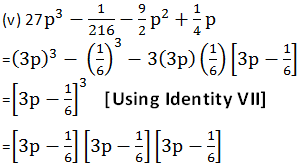
9
(i) x3 + y3 = (x + y) (x2 - xy + y2)
(ii) x3 - y3 = (x - y) (x2 + xy + y2)
Answer
(i) R.H.S. = (x + y)(x2 – xy + y2)
= x(x2 – xy + y2) + y(x2 – xy + y2)
= x3 – x2y + xy2 + x2y – xy2 + y3
= x3 + y3 = L.H.S.
(ii) R.H.S. = (x – y)(x2 + xy + y2)
= x(x2 + xy + y2) – y(x2 + xy + y2)
= x3 + x2y + xy2 – x2y – xy2 – y3
= x3 – y3 = L.H.S.
10
(i) 27y3 + 125z3
(ii) 64m3 - 343n3
Answer
REMEMBER
I. x3 + y3 = (x + y)(x2 + y2 – xy)
II. x3 – y3 = (x – y)(x2 + y2 + xy)
(i) Using the identity (x3 + y3) = (x + y)(x2 – xy + y2),
We have 27y3 + 125z3 = (3y)3 + (5z)3
= (3y + 5z) [(3y)2 – (3y)(5z) + (5z)2]
= (3y + 5z)(9y2 – 15yz + 25z2
(ii) Using the identity x3 – y3 = (x – y)(x2 + xy + y2),
We have 64m3 – 343n3
= (4m)3 – (7n)3
= (4m – 7n)[(4m)2 + (4m)(7n) + (7n)2]
= (4m – 7n)(16m2 + 28mn + 49n2)
11
Answer
REMEMBERx3 + y3 + z3 – 3xyz = (x + y + z)(x2 + y2 + z2 – xy – yz – zx)
We have 27x3 + y3 + z3 – 9xyz = (3x)3 + (y)3 + (z)3 – 3(3x)(y)(z)
∴ Using the identity x3 + y3 + z3 – 3xyz = (x + y + z)(x2 + y2 + z2 – xy – yz – zx),
We have (3x)3 + (y)3 + (z)3 – 3(3x)(y)(z)
= (3x + y + z)[(3x)2 + y2 + z2 – (3x x y) – (y x z) – (z x 3x)]
= (3x + y + z)(9x2 + y2 + z2 – 3xy – yz – 3zx)
12
Answer
R.H.S. = 1/2 (x + y + z)[(x – y)2 + (y – z)2 + (z – x)2]= 1/2 (x + y + z)[(x2 + y2 – 2xy) + (y2 + z2 –2yz) + (z2 + x2 – 2xz)]
= 1/2 (x + y + z)[x2 + y2 + y2 + z2 + z2 + x2 – 2xy – 2yz – 2zx]
= 1/2 (x + y + z)[2(x2 + y2 + z2 – xy – yz – zx)]
= 2 x 1/2 x (x + y + z)(x2 + y2 + z2 – xy – yz – zx)
= (x + y + z)(x2 + y2 + z2 – xy – yz – zx)
= x3 + y3 + z3 – 3xyz = L.H.S.
13
Answer
Since x + y + z = 0∴ x + y = –z or (x + y)3
= (–z)3 or x3 + y3 + 3xy(x + y)
= –z3 or x3 + y3 + 3xy(–z)
= –z3 [∵ x + y = (–z)]
or x3 + y3 – 3xyz = –z3
or (x3 + y3 + z3) – 3xyz
= 0 or (x3 + y3 + z3) = 3xyz
Hence, if x + y + z = 0, then (x3 + y3 + z3) = 3xyz.
14
(i) (-12)3 + (7)3 + (5)3
(ii) (28)3 + (–15)3 + (-13)3
Answer
(i) (–12)3 + (7)3 + (5)3
Let x = –12, y = 7 and z = 5
Then x + y + z = –12 + 7 + 5 = 0
We know that if x + y + z = 0, then x3 + y3 + z3 = 3xyz.
∴ (–12)3 + (7)3 + (5)3
= 3 [(–12)(7)(5)] [∵ (–12) + 7 + 5 = 0]
= 3[–420]
= –1260
Thus, (–12)3 + (7)3 + (5)3 = –1260
(ii) (28)3 + (–15)3 + (–13)3
Let x = 28, y = –15 and z = –13
∴ x + y + z = 28 – 15 – 13 = 0
We know that if x + y + z = 0,
then x3 + y3 + z3 = 3xyz.
∴ (28)3 + (–15)3 + (–13)3
= 3(28)(–15)(–13) [∵ 28 + (–15) + (–13) = 0]
= 3(5460)
= 16380
Thus, (28)3 + (–15)3 + (–13)3 = 16380
15
(i) Area : 25a2 - 35a + 12
(ii) Area : 35 y2 + 13y - 12
Answer
REMEMBER
Area of a rectangle = (Length) x (Breadth)
(i) Area = 25a2 – 35a + 12
We have to factorise the polynomial: 25a2 – 35a + 12
Splitting the co-efficient of a, we have –35 = (–20) + (–15)
[∵ 25 x 12 = 300 and (–20) x (–15)= 300]
= 25a2 – 35a + 12 = 25a2 – 20a – 15a + 12
∴= 5a(5a – 4) – 3(5a – 4) = (5a – 4)(5a – 3)
Thus, the possible length and breadth are (5a – 3) and (5a – 4).
(ii) Area = 35y2 + 13y – 12
We have to factorise the polynomial 35y2 + 13y – 12.
Splitting the middle term, we get 13y = 28y – 15y
[∵ 28 x (–15)= –420 and –12 x 35 = – 420]
∴ 35y2 + 13y – 12
= 35y2 + 28y – 15y – 12
= 7y(5y + 4) –3(5y + 4)
= (5y + 4)(7y – 3)
Thus, the possible length and breadth are (7y – 3) and (5y + 4).
16
(i) Volume : 3x2 - 12x
(ii) Volume : 12ky2 + 8ky - 20k
Answer
REMEMBER
Volume of a cuboid = (Length) x (Breadth) x (Height)
(i) Volume = 3x2 – 12x On factorising 3x2 – 12x,
we have 3x2 – 12x = 3[x2 – 4x]
= 3[x(x – 4)] = 3x (x – 4)
∴ The possible dimensions of the cuboid are: 3, x and (x – 4) units.
(ii) Volume = 12ky2 + 8ky – 20k
We have 12ky2 + 8ky – 20k
= 4[3ky2 + 2ky – 5k]
= 4[k(3y2 + 2y – 5)]
= 4k[3y2 – 3y + 5y – 5] (Splitting the middle term)
= 4k[3y(y – 1) + 5(y – 1)]
= 4k[(3y + 5)(y – 1)]
= 4k x (3y + 5) x (y – 1)
Thus, the possible dimensions are: 4k, (3y + 5) and (y – 1) units.