NCERT Solutions for Chapter 1 Number System Class 9 Maths

1

Is zero a rational number? Can you write it in the form p/q , where p and q are integers and q ≠ 0?

Answer

Yes, zero is a rational number. We can write it in the form (p/q).

Exercise 1.1 Page Number 5

2

Find six rational numbers between 3 and 4.

Answer

We know that there are an infinite number of rational numbers between two rational numbers. Therefore, six rational numbers between 3 and 4 can be:
Let x = 3 and y = 4, also n = 6

Since, the six rational numbers between x and y are:
(x + d), (x + 2d), (x + 3d), (x + 4d), (x + 5d) and (x + 6d).
∴ The six rational numbers between 3 and 4 are:

Exercise 1.1 Page Number 5

3

Find five rational numbers between (3/5) and (4/5).

Answer

Let x = (3/5), y = (4/5) and n = 5

Exercise 1.1 Page Number 5

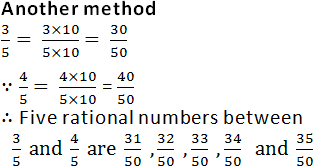
4(i)

State whether the following statements are true or false. Give reasons for your answers.
Every natural number is a whole number.

Answer

True statement [∵ The collection of all natural numbers and 0 is called whole numbers]

Exercise 1.1 Page Number 5

4(ii)

State whether the following statements are true or false. Give reasons for your answers.
Every integer is a whole number.

Answer

False statement [∵ Integers such as –1, –2 are non-whole numbers]

Exercise 1.1 Page Number 5

4(iii)

State whether the following statements are true or false. Give reasons for your answers.
Every rational number is a whole number.

Answer

False statement [∵ Rational number (1/2) is not a whole number]

Exercise 1.1 Page Number 5

1(i)

State whether the following statements are true or false. Justify your answers.
Every irrational number is a real number.

Answer

True statement, because all rational numbers and all irrational numbers form the group (collection) of real numbers.

Exercise 1.2 Page Number 8

1(ii)

State whether the following statements are true or false. Justify your answers.
Every point on the number line is of the form √m, where m is a natural number.

Answer

False statement, because no negative number can be the square root of any natural number.

Exercise 1.2 Page Number 8

1(iii)

State whether the following statements are true or false. Justify your answers.
Every real number is an irrational number.

Answer

False statement, because rational numbers are also a part of real numbers.

Exercise 1.2 Page Number 8

2

Are the square roots of all positive integers irrational? If not, give an example of the square root of a number that is a rational number.

Answer

No, if we take a positive integer, say 4 its square root is 2, which is a rational number.

Also, 4 is a rational number.

Exercise 1.2 Page Number 8

3

Show how √5 can be represented on the number line.

Answer

Let us take the horizontal line XOX" as the x-axis. Mark O as its origin such that it represents 0.
OA = 1 unit, AB = 1 unit.
∴ OB = 2 units

Draw a perpendicular, BC ⊥ OX.

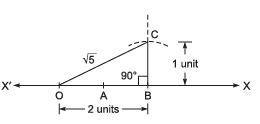
Ex 1.2 NCERT Solutions - Number System
Cut off BC = 1 unit.
Since OBC is a right triangle.
∴ OB² + OC² = OC²
or 2² + 1² = OC² or 4 + 1 = OC²
or, OC² = 5
⇒ OC = √5
With O as centre and OC as radius, draw an arc intersecting OX at D.
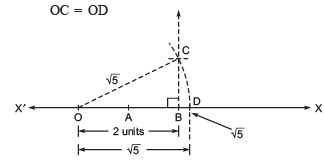
Since,

OC = OD

∴ OD represents √5 on XOX'.

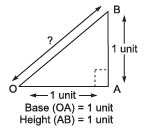
Ex 1.2 NCERT Solutions - Number System

Remember
According to the Pythagoras theorem,

In a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
In the figure: OB² =OA² + AB²
⇒ OB² =1² + 1² = 2

⇒ OB = √2

Ex 1.2 NCERT Solutions - Number System

Exercise 1.2 Page Number 8

4

Classroom activity (Constructing the ‘square root spiral’)

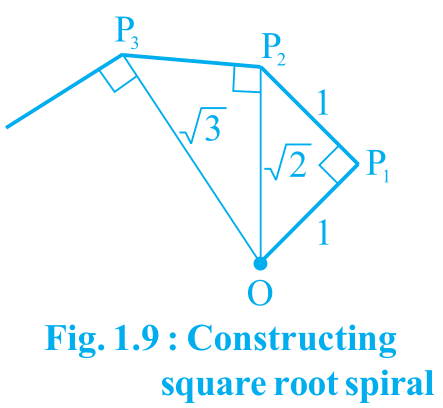
Answer

Take a large sheet of paper and construct the ‘square root spiral’ in the following fashion. Start with a point O and draw a line segment OP₁ of unit length. Draw a line segment P₁P₂ perpendicular to OP₁ of unit length (see Fig. 1.9). Now draw a line segment P₂P₃ perpendicular to OP₂. Then draw a line segment P₃P4 perpendicular to OP₃. Continuing in this manner, you can get the line segment P_n–1P_n by drawing a line segment of unit length perpendicular to OP_n–1. In this manner, you will have created the points P₂ , P₃ ,...., P_n ,... ., and joined them to create a beautiful spiral depicting √2, √3, √4, ...

Exercise 1.2 Page Number 8

1(i)

Write the following in decimal form and say what kind of decimal expansion each has:
36/100

Answer

We have 36/100 = 0.36
∴ the decimal expansion of 36/100 is terminating.

Exercise 1.3 Page Number 14

1(ii)

Write the following in decimal form and say what kind of decimal expansion each has:
1/11

Answer

Dividing 1 by 11, we have: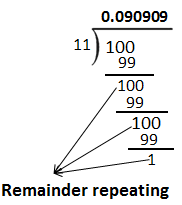

∴ Thus, the decimal expansion is “non-terminating repeating”.

Note: The bar above the digits indicates the block of digits that repeats. Here, the repeating block is 09.

Exercise 1.3 Page Number 14

1(iii)

Write the following in decimal form and say what kind of decimal expansion each has:
$D:\Work\sunny\class 9 math ncert solutions\ncert solutions for chapter 1\3_files\image006.png$

Answer

To write $D:\Work\sunny\class 9 math ncert solutions\ncert solutions for chapter 1\3_files\image018.png$ in p/q from, we have

$D:\Work\sunny\class 9 math ncert solutions\ncert solutions for chapter 1\3_files\image020.png$
Now, dividing 33 by 8, we have

$D:\Work\sunny\class 9 math ncert solutions\ncert solutions for chapter 1\3_files\image022.jpg$

Remainder = 0, means the process of division terminates.

$D:\Work\sunny\class 9 math ncert solutions\ncert solutions for chapter 1\3_files\image024.png$

∴ Thus, the decimal expansion is terminating.

Exercise 1.3 Page Number 14

1(iv)

Write the following in decimal form and say what kind of decimal expansion each has:
3/13

Answer

Dividing 3 by 13, we have

$D:\Work\sunny\class 9 math ncert solutions\ncert solutions for chapter 1\3_files\image026.jpg$

3 came as a remainder. The dividend in first case was 3. So, the block of digits will repeat again.

Here, the repeating block of digits is 230769.

$D:\Work\sunny\class 9 math ncert solutions\ncert solutions for chapter 1\3_files\image028.png$

∴ Thus, the decimal expansion of 3/13 is “non-terminating repeating”.

Exercise 1.3 Page Number 14

1(v)

Write the following in decimal form and say what kind of decimal expansion each has:
2/11

Answer

Dividing 2 by 11, we have

$D:\Work\sunny\class 9 math ncert solutions\ncert solutions for chapter 1\3_files\image030.jpg$

Here, the repeating block of digits is 18.

$D:\Work\sunny\class 9 math ncert solutions\ncert solutions for chapter 1\3_files\image032.png$

∴ Thus, the decimal expansion of 2/11 is “non-terminating repeating”.

Exercise 1.3 Page Number 14

1(vi)

Write the following in decimal form and say what kind of decimal expansion each has:
329/400

Answer

Dividing 329 by 400, we have

$D:\Work\sunny\class 9 math ncert solutions\ncert solutions for chapter 1\3_files\image034.jpg$

Remainder = 0, means the process of division terminates.

$D:\Work\sunny\class 9 math ncert solutions\ncert solutions for chapter 1\3_files\image036.png$

∴ Thus, the decimal expansion of 329/400 is terminating.

Exercise 1.3 Page Number 14

2

You know that $D:\Work\sunny\class 9 math ncert solutions\ncert solutions for chapter 1\3_files\image038.png$ Can you predict what the decimal expansions of 2/7, 3/7, 4/7, 5/7, 6/7 are, without actually doing the long division? If so, how?

Answer

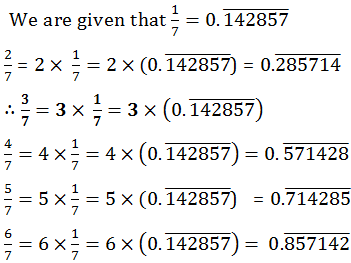
Thus, without actually doing the long division we can predict the decimal expansions of the above given rational numbers.

Exercise 1.3 Page Number 14

3

Express the following in the form (p\q) , where p and q are integers and q ≠ 0.

Answer

(i) Let x = = 0.6666… Since, there is one repeating digit.
∴ We multiply both sides by 10,
10x = (0.666…) x 10
or 10x = 6.6666…
∴ 10x - x = 6.6666... - 0.6666...
or 9x = 6
or x = 6/9 = 2/3

(ii) Let X = 0.4777....
∴ 10x = 10× (0.4777 ... )
or 10x = 4.777 ...(1)
and 100x = 47.777 ...(2)
Subtracting (1) from (2), we have
100x – 10x = (47.777…) – (4.777…)
90x = 43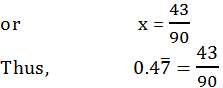

(iii) Let = 0.001001.... ...(1)
Here, we have three repeating digits after the decimal point, therefore we multiply by 1000.
∴ 1000x = 1000 = 1000×0.001001...
or 1000x = 1.001001… ...(2)
Subtracting (1) from (2), we have
1000x – x = (1.001…) – (0.001…)
or 999x = 1
∴ x = 1/999

Exercise 1.3 Page Number 14

4

Express 0.99999… in the form p/q . Are you surprised by your answer? With your teacher and classmates discuss why the answer makes sense.

Answer

Let x = 0.99999... ...(1)
Multiply both sides by 10,
we have [∵ There is only one repeating digit.]
10 x x = 10 x (0.99999…)
or 10x = 9.9999 ...(2)
Subtracting (1) from (2),
we get 10x – x = (9.9999…) – (0.9999…)
or 9x = 9
or x = 9/9 = 1
Thus, 0.9999… = 1
As 0.9999… goes on forever, there is no gap between 1 and 0.9999
Hence both are equal.

Exercise 1.3 Page Number 14

5

What can the maximum number of digits be in the repeating block of digits in the decimal expansion of (1/17)? Perform the division to check your answer.

Answer

Since, the number of entries in the repeating block of digits is less than the divisor.
In 1/17, the divisor is 17.
∴ The maximum number of digits in the repeating block is 16. To perform the long division, we have

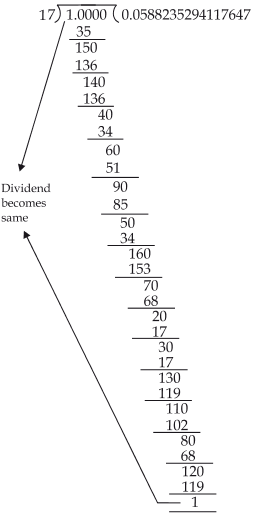
The remainder 1 is the same digit from which we started the division.

Thus, there are 16 digits in the repeating block in the decimal expansion of 1/17. Hence, our answer is verified.

Exercise 1.3 Page Number 14

6

Look at several examples of rational numbers in the form p/q (q ≠ 0), where p and q are integers with no common factors other than 1 and having terminating decimal representations (expansions). Can you guess what property q must satisfy?

Answer

Let us look at decimal expansion of the following terminating rational numbers:

We observe that the prime factorization of q (i.e. denominator) has only powers of 2 or powers of 5 or powers of both.
Note: If the denominator of a rational number (in its standard form) has prime factors either 2 or 5 or both, then and only then it can be represented as a terminating decimal.

Exercise 1.3 Page Number 14

7

Write three numbers whose decimal expansions are non-terminating non-recurring.

Answer

√2=1.414213562…
√3= 1.732050808…
√5=2.236067978 …

Exercise 1.3 Page Number 14

8

Find three different irrational numbers between the rational numbers (5/7) and (9\11).

Answer

To express decimal expansion of 5/7 and 9/11, we have: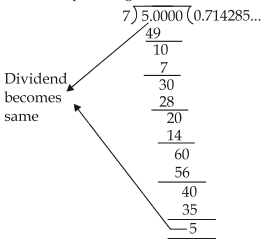

As there are an infinite number of irrational numbers between

any three of them can be:
(i) 0.750750075000750…
(ii) 0.767076700767000767…
(iii) 0.78080078008000780…

Exercise 1.3 Page Number 14

9

Classify the following numbers as rational or irrational:
(i) √23
(ii)√225
(iii) 0.3796
(iv) 7.478478
(v) 1.101001000100001…

Answer

(i) ∵ 23 is not a perfect square.
∴ is an irrational number.
(ii) ∵ √225 = 15 x 15 = 152
∴ 225 is a perfect square.
Thus, 225 is a rational number.
(iii) ∵ 0.3796 is a terminating decimal,
∴ It is a rational number.
(iv) 7.478478… =

is a non-terminating and recurring (repeating) decimal.
∴ It is a rational number.
(v) Since, 1.101001000100001… is a non-terminating and non-repeating decimal number.
∴ It is an irrational number.

Exercise 1.3 Page Number 14

1

Visualise 3.765 on the number line, using successive magnification.

Answer

3.765 lies between 3 and 4.
Let us divide the interval (3, 4) into 10 equal parts.

Since, 3.765 lies between 3.7 and 3.8. We again magnify the interval [3.7, 3.8] by dividing it further into 10 parts and concentrate the distance between 3.76 and 3.77.
The number 3.765 lies between 3.76 and 3.77. Therefore we further magnify the interval [3.76, 3.77] into 10 equal parts.
Now, the point corresponding to 3.765 is clearly located, as shown in Fig. (iii) above.

Exercise 1.4 Page Number 18

2

Visualise on the number line, up to 4 decimal places.

Answer

Note: We can magnify an interval endlessly using successive magnification.
To visualize 4. or 4.2626… on the number line up to 4 decimal places, we use the following steps.
(i) . The number 4.2626… lies between 4 and 5. Divide the interval [4, 5] in 10 smaller parts:

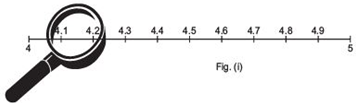
(ii) . Obviously, the number 4.2626... lies between 4.2 and 4.3. We magnify the interval [4.2, 4.3]:

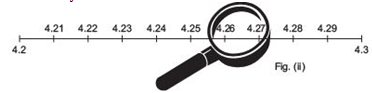
(iii) . Next, we magnify the interval [4.26, 4.27]:

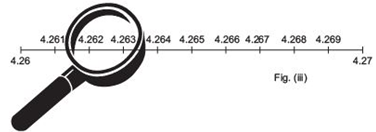
(iv) . Finally magnify the interval [4.262, 4.263]:

In Fig. (iv), we can easily observe the number 4.2626… or

Exercise 1.4 Page Number 18

1

Classify the following numbers as rational or irrational
(i) 2-√5
(ii) (3 + √23 ) -√23
(iii) (2√7)/(7√7)
(iv) 1/√2
(v) 2π

Answer

i) 2 –√5
Since it is a difference of a rational and irrational number,
∴ 2 –√5 is an irrational number.

(ii) (3 + √23 ) - √23
We have (3 + √23 ) - √23 = 3 + √23 - √23 = 3 which is a rational number
∴ (3 + √23 ) - √23 is a rational number

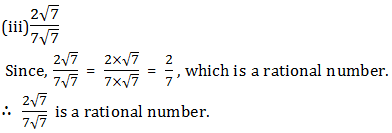
(iv) 1/√2
∵The quotient of rational and irrational is an irrational number.
∴ 1/√2 is an irrational number.
( v )2π
∵ 2π = 2 x π = Product of a rational and an irrational (which is an irrational number)
∴ 2π is an irrational number.

REMEMBER
For real numbers a, b, c and d, we have:
(i) √ab = √a . √b
(ii) √(a/b)= √a/√b
(iii) (√a+√b ) (√a- √b) = a- b
(iv) (a+√b) (a-√b) = a^2-b
(v) (√a+√b) (√c +√d) = √ac+√ad +√bc+ √bd
(vi) (√a+ √b)^2 = a+2√ab+b

Exercise 1.5 Page Number 24

2

Simplify each of the following expressions:
(i) (3+ √3)(2+ √2)
(ii) (3+√3)(3-√3)
(iv) (√5+ √2)^2
(v) (√5- √2) (√5+√2)

Answer

(i) (3+ √3)(2+√2) - 2(3 +√3 ) + √2 (3 +√3)
= (2 x 3 + 2√3 ) + (3√2 +√2 x √3 )
= 6 + 2√3 + 3√2 + √6
Thus, (3 +√3 )(2 +√2 )
= 6 + 2√3 + 3√2 +√6

(ii) (3 +√3 )(3 – √3 )
= (3)² – ( √3)²[∵ (a + b)(a – b) = a² – b²]
= 3² – 3
= 9 – 3 = 6
∴ (3 + √3 ) (3 – √3 ) = 6.

(iii) ( √5 +√2 )²
= (√5 )² + (√2)² + 2( √5)(√2)
[∵ (a + b)² = a² + b² + 2ab]
= 5+2+2√10
= 7+2√10
∴(√5+√2)² =7+ 2√10

(iv) ( √5 – √2 )( √5 + √2)
= (√5 )² – (√2 )² [∵ (a + b)(a – b) = a² – b²]
= 5 – 2 = 3
∴ ( √5 – √2 )( √5 + √2) = 3

Exercise 1.5 Page Number 24

3

Recall, π is defined as the ratio of the circumference (say c) of a circle to its diameter (say d). That is, π = c/d . This seems to contradict the fact that π is irrational. How will you resolve this contradiction?

Answer

When we measure the length of a line with a scale or with any other device, we only get an approximate rational value, i.e. c and d both are irrational.
∴ c/d is irrational and hence π is irrational. Thus, there is no contradiction in saying that π is irrational.

Exercise 1.5 Page Number 24

4

Represent √9.3 on the number line.

Answer

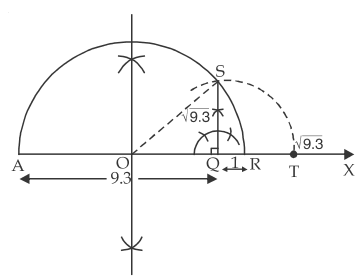
(i) Draw a ray AX.

(ii) Mark a point Q on the ray such that AQ = 9.3 units.

(iii) From Q, mark a point R such that QR =1 unit.

(iv) Draw perpendicular bisector of AR to obtain mid-point. Let us mark it as O.

(v) Taking O as centre and OR as radius draw a semicircle.

(vi) Draw QS ⊥ AX which cuts semicirle at S.

(vii) Taking Q as centre and QS as radius draw an arc cutting AX at T. Then QT = QS =√9.3

Exercise 1.5 Page Number 24

5

Rationalise the denominators of the following:
(i) 1/√7
(ii) 1/(√7-√6)
(iii) 1/(√5+√2)
(iv) 1/(√7-2)

Answer

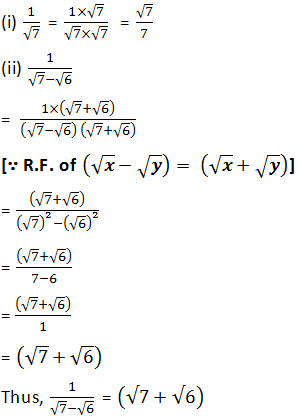
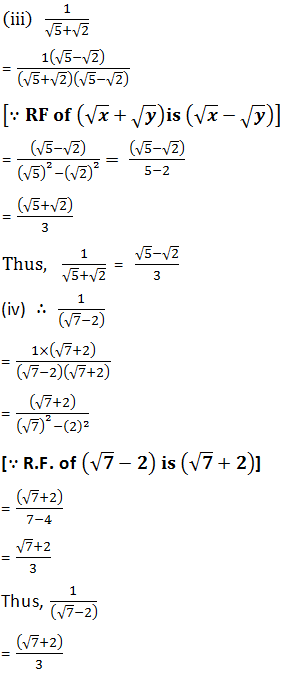
Exercise 1.5 Page Number 24

1

Find:
(i) 64^1/2
(ii) 32^1/5
(iii) 125^1/3

Answer

(i) ∵ 64 = 8 x 8 = 8²
∴ (64)^1/2
= (8²)^1/2 = 8^2x1/2
[∵ (a^m)ⁿ = a^m x ⁿ]
= 8¹ = 8
Thus, 64^1/2 = 8

(ii) ∵ 32 = 2 x 2 x 2 x 2 x 2 = 2⁵
∴ (3₂)^1/5 = (2⁵)^1/5
= 2^5x1/5 [∵ (a^m)ⁿ = a^mn]
= 2¹ = 2
Thus, (32)^1/5 = 2

(iii) ∵ 125 = 5 x 5 x 5 = 53
∴ (125)^1/3 = (5³)^1/3
= 5^3x1/3= 5¹Thus, 125^1/3 = 5

Exercise 1.6 Page Number 26

2

Find:
(i) 9^3/2
(ii) 32^2/5
(iii) 16^3/4
(iv) 125^–1/3

Answer

(i) ∵ 9 = 3 x 3 = 3²
∴ (9)^3/2 = (3²)^3/2
= 3^{2 x 3/2}= 3³ = 27
Thus, 9^3/2 = 27

(ii) ∵ 32 = 2 x 2 x 2 x 2 x 2 = 2⁵
∴ (32)^2/5 = (2⁵)^2/5
= 2^5x2/5
= 2² = 4
Thus, 32^2/5 = 4

(iii) ∵ 16 = 2 x 2 x 2 x 2 = 2⁴
∴ (16)^3/4 = (2⁴)^3/4
= 2^4x3/4 = 2³ = 8
Thus, 16^3/4= 8

(iv) ∵ 125 = 5 x 5 x 5 = 5³
∴ (125)^–1/3 = (5³)^–1/3
= 5^3x(–1/3)
= 5–1 = 1/5

Exercise 1.6 Page Number 26

3

Simplify:

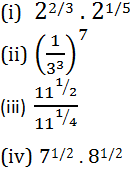
Answer

(i) ∵ a^m . aⁿ = a^m+n
∴ 2^2/3 . 2^1/5 = 2^{2/3 + 1/5}

= 2^13/15

(ii) ∵ 1/a^m = a^−m and (a^−m)ⁿ
= a^−mn = 1/a^mn
∴ (1/3³ )⁷ = (3⁻³ )⁷
= 3^−3×7= 3⁻²¹
= 1/3²¹
Thus, (1/3³ )⁷ = 1/3²¹

(iii) 11^1⁄2/11^1⁄4
= 11^1⁄2÷ 11^1⁄4
= 11^1⁄2^{− 1⁄4}[∵ a^m/aⁿ = a^m⁻ⁿ]
= 11^1⁄4Thus,
11^1⁄2/11^1⁄4 = 11^1⁄4

(iv) ∵ a^m . b^m = (ab)^m∴ 7^1/2 . 8^1/2
= (7 x 8)^1/2
= (56)^1/2Thus,
7^1/2 . 8^1/2= (56)^1/2

Exercise 1.6 Page Number 26

Number System

NCERT Solutions for Chapter 1 Number System Class 9 Maths

1

2

3

4(i)

4(ii)

4(iii)

1(i)

1(ii)

1(iii)

2

3

4

1(i)

1(ii)

1(iii)

1(iv)

1(v)

1(vi)

2

3

4

5

6

7

8

9

1

2

1

2

3

4

5

1

2

3

FAQ (Frequently Asked Questions

Related Chapters

Related Questions