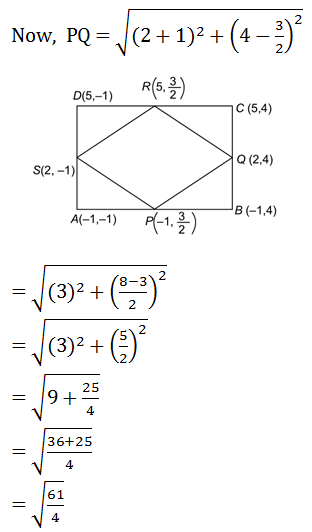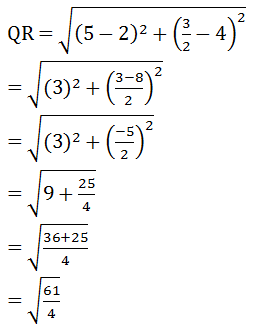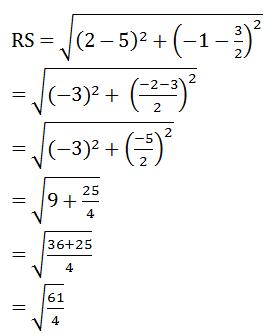NCERT Solutions for Chapter 7 Coordinate Geometry Class 10 Maths
Book Solutions1
Find the distance between the following pairs of points:
(i) (2, 3), (4, 1)
(ii) (−5, 7), (−1, 3)
(iii) (a, b), (− a, − b)
Answer
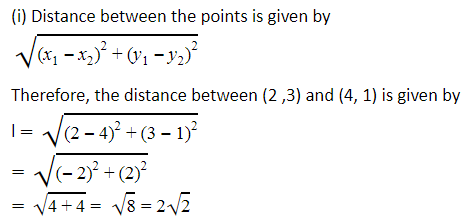
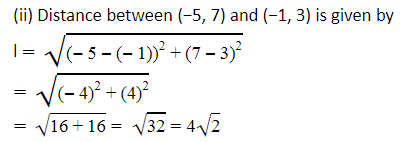
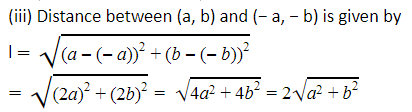
2
Answer
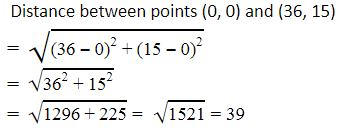
Yes, Assume town A at origin point (0, 0).
Therefore, town B will be at point (36, 15) with respect to town A.
And hence, as calculated above, the distance between town A and B will be 39 km.
3
Answer
Let the points (1, 5), (2, 3), and (- 2,-11) be representing the vertices A, B, and C of the given triangle respectively.Let A = (1, 5), B = (2, 3) and C = (- 2,-11)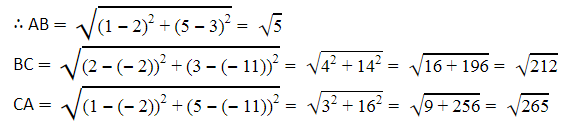
Since AB + BC ≠ CA
Therefore, the points (1, 5), (2, 3), and ( - 2, - 11) are not collinear.
4
Answer
Let the points (5, - 2), (6, 4), and (7, - 2) are representing the vertices A, B, and C of the given triangle respectively.
5
Using distance formula, find which of them is correct.
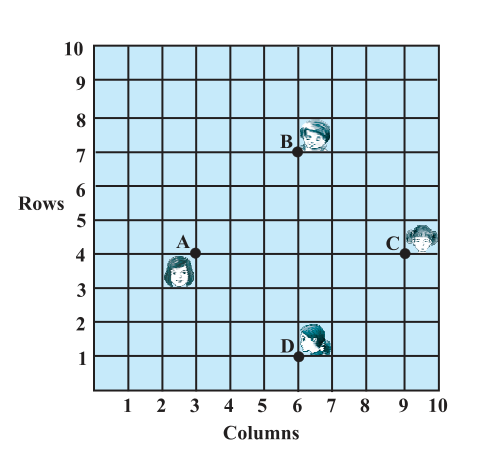
Answer
Clearly from the figure, the coordinates of points A, B, C and D are (3, 4), (6, 7), (9, 4) and (6, 1).By using distance formula, we get
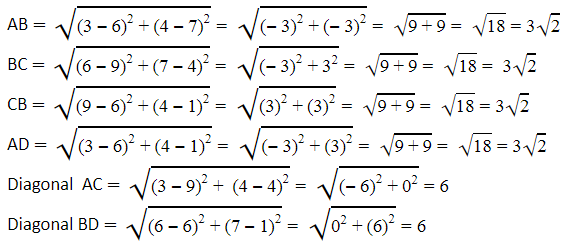
It can be observed that all sides of this quadrilateral ABCD are of the same length and also the diagonals are of the same length.
Therefore, ABCD is a square and hence, Champa was correct.
6
answer:
(i) (- 1, - 2), (1, 0), (- 1, 2), (- 3, 0)
(ii) (- 3, 5), (3, 1), (0, 3), (- 1, - 4)
(iii) (4, 5), (7, 6), (4, 3), (1, 2)
Answer
(i) Let the points ( - 1, - 2), (1, 0), ( - 1, 2), and ( - 3, 0) be representing the vertices A, B, C, and D of the given quadrilateral respectively.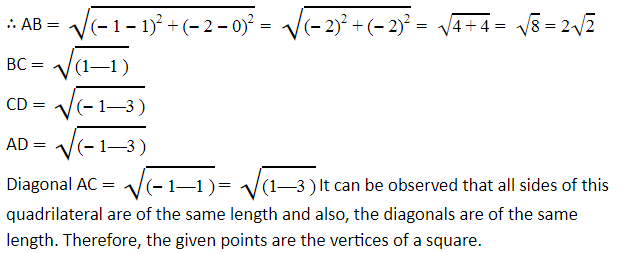
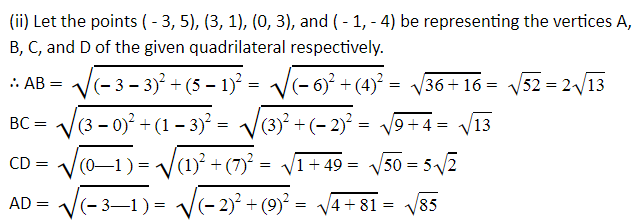
It can be observed that all sides of this quadrilateral are of different lengths.
Therefore, it can be said that it is only a general quadrilateral, and not specific such as square, rectangle, etc.
(iii) Let the points (4, 5), (7, 6), (4, 3), and (1, 2) be representing the vertices A, B, C, and D of the given quadrilateral respectively.
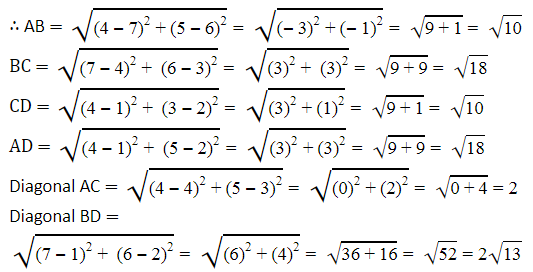
It can be observed that opposite sides of this quadrilateral are of the same length. However, the diagonals are of different lengths. Therefore, the given points are the vertices of a parallelogram.
7
Answer
We have to find a point on x-axis. Therefore, its y-coordinate will be 0.Let the point on x-axis be (x,0)
Distance between (x , 0 ) and (2 , −5) =
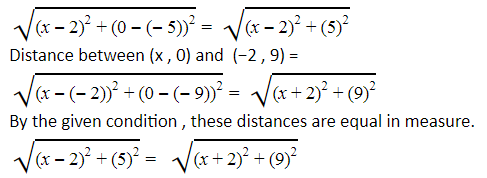
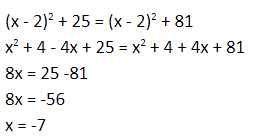
Therefore, the point is ( - 7, 0).
8
Answer
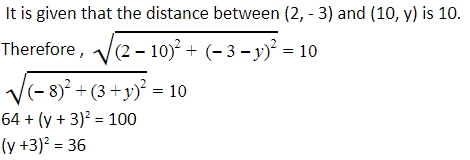
y + 3 = ±6
y + 3 = +6 or y + 3 = -6
Therefore, y = 3 or -9
9
Answer
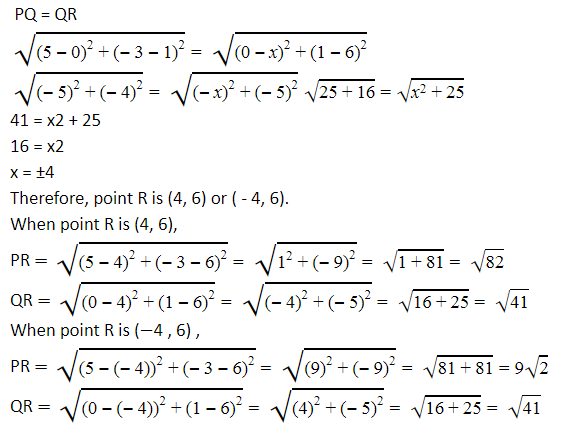
10
Answer
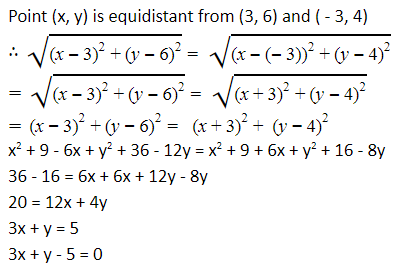
1
Answer
Let P(x, y) be the required point. Using the section formula, we get
Therefore, the point is (1, 3).
2
Answer
Let P (x1, y1) and Q (x2, y2) are the points of trisection of the line segment joining the given points i.e., AP = PQ = QB
Therefore, point P divides AB internally in the ratio 1:2.
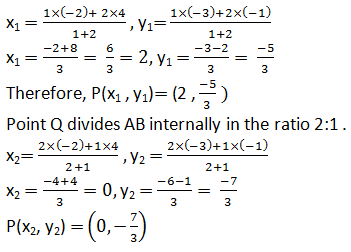
3
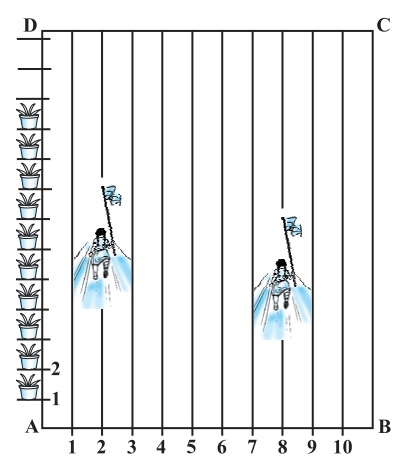
Answer
It can be observed that Niharika posted the green flag at 1/4th of the distance AD i.e., (1×100/4)m = 25m from the starting point of 2nd line. Therefore, the coordinates of this point G is (2, 25).Similarly, Preet posted red flag at of the distance AD i.e., (1× 100/5) m = 20m from the starting point of 8th line. Therefore, the coordinates of this point R are (8, 20).
Distance between these flags by using distance formula = GR

Therefore, Rashmi should post her blue flag at 22.5m on 5th line.
4
Answer
Let the ratio in which the line segment joining ( -3, 10) and (6, -8) is divided by point ( -1, 6) be k : 1.Therefore,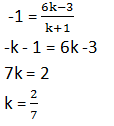
Therefore, the required ratio is 2:7.
5
Answer
Let the ratio in which the line segment joining A (1, - 5) and B ( - 4, 5) is divided by x-axis be k:1 .
6
Answer
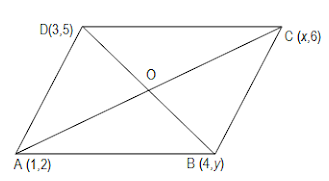
Let A,B,C and D be the points (1,2) (4,y), (x,6) and (3,5) respectively.
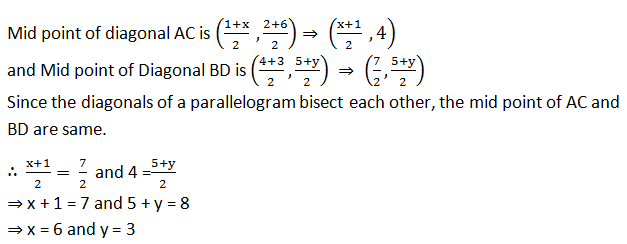
7
Answer
Let the coordinates of point A be (x, y).Mid-point of AB is (2, - 3), which is the center of the circle.
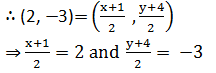
⇒ x + 1 = 4 and y + 4 = -6
⇒ x = 3 and y = -10
Therefore, the coordinates of A are (3,-10).
8
Answer
The coordinates of point A and B are (-2,-2) and (2,-4) respectively.
Since AP = 3/7 AB
Therefore, AP:PB = 3:4
Point P divides the line segment AB in the ratio 3:4.
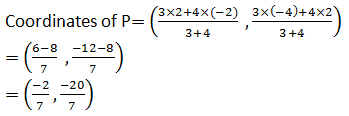
9
Answer
From the figure, it can be observed that points X, Y, Z are dividing the line segment in a ratio 1:3, 1:1, 3:1 respectively.
10
[Hint: Area of a rhombus = 1/2(product of its diagonals)]
Answer
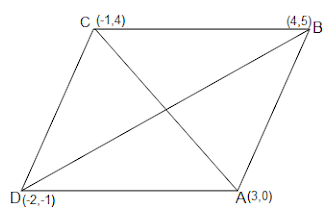
Let (3, 0), (4, 5), ( - 1, 4) and ( - 2, - 1) are the vertices A, B, C, D of a rhombus ABCD.
1
(i) (2, 3), (-1, 0), (2, -4)
(ii) (-5, -1), (3, -5), (5, 2)
Answer
(i) Area of a triangle is given by
= 1/2 {x1 (y2 - y3)+ x2 (y3 - y1)+ x3 (y1 - y2)}
= 1/2 [2 { 0- (-4)} + (-1) {(-4) - (3)} + 2 (3 - 0)]
= 1/2 {8 + 7 + 6}
= 21/2 square units.
(ii) Area of the given triangle
= 1/2 [-5 { (-5)- (4)} + 3(2-(-1)) + 5{-1 - (-5)}]
= 1/2{35 + 9 + 20}
= 32 square units
2
(i) (7, -2), (5, 1), (3, -k)
(ii) (8, 1), (k, -4), (2, -5)
Answer
(i) For collinear points, area of triangle formed by them is zero.
Therefore, for points (7, -2) (5, 1), and (3, k), area = 0![]()
7 - 7k + 5k +10 -9 = 0
-2k + 8 = 0
k = 4
(ii) For collinear points, area of triangle formed by them is zero.
Therefore, for points (8, 1), (k, - 4), and (2, - 5), area = 0![]()
8 - 6k + 10 = 0
6k = 18
k = 3
3
Answer
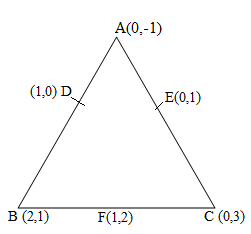
Let the vertices of the triangle be A (0, -1), B (2, 1), C (0, 3).
Let D, E, F be the mid-points of the sides of this triangle. Coordinates of D, E, and F are given by.
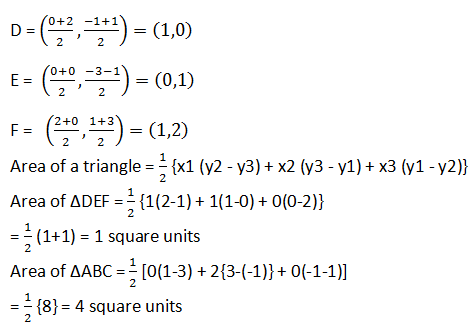
Therefore, the required ratio is 1:4.
4
Answer
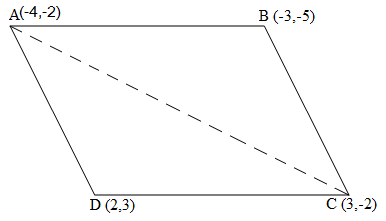
Let the vertices of the quadrilateral be A (- 4, -2), B (-3, -5), C (3, -2), and D (2, 3).
Join AC to form two triangles ΔABC and ΔACD.
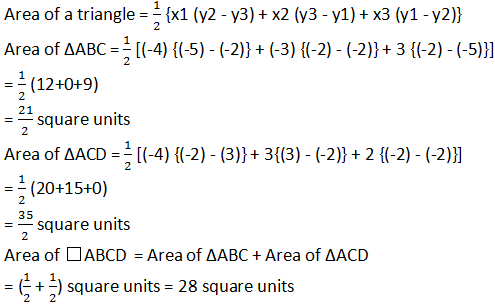
5
Answer
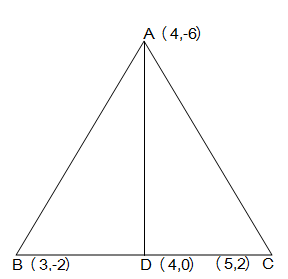
Let the vertices of the triangle be A (4, -6), B (3, -2), and C (5, 2).
Let D be the mid-point of side BC of ΔABC. Therefore, AD is the median in ΔABC.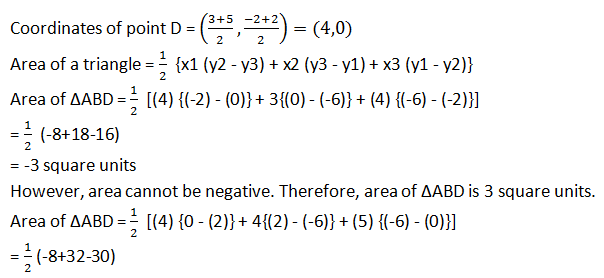
= -3 square units
However, area cannot be negative. Therefore, area of ΔABD is 3 square units.
The area of both sides is same. Thus, median AD has divided ΔABC in two triangles of equal areas.
1
Answer
Let the line 2x+ y – 4 = 0 divides the line segment joining the points A (2 , −2) and B(3, 7) in the ratio k:1 at the point P.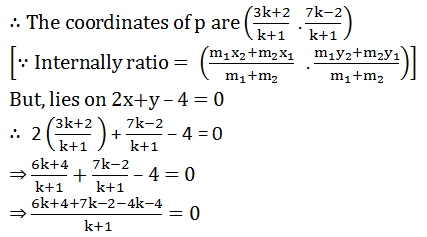
⇒ 6k + 4+7k – 2 –4k – 4 = 0
⇒ 9k – 2 = 0
⇒ 9k = 2
⇒ k = 2/9
∴ Point p divides the line in the ratio 2:9.
2
Answer
Since, the point A(x, y), B(1, 2) and c (7 , 0) are collinear .∴ Area of ∆ ABC = 0
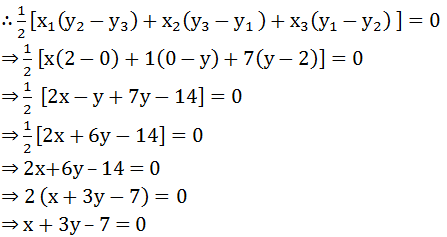
3
Answer
Let C(x, y) be the centre of the circle passing through the points P(6,−6), Q (3, −7) and R (3, 3) .Then PC = QC = CR (Radius of circle )
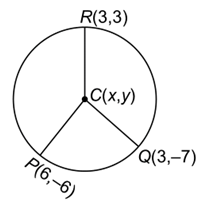
Now PC = QC
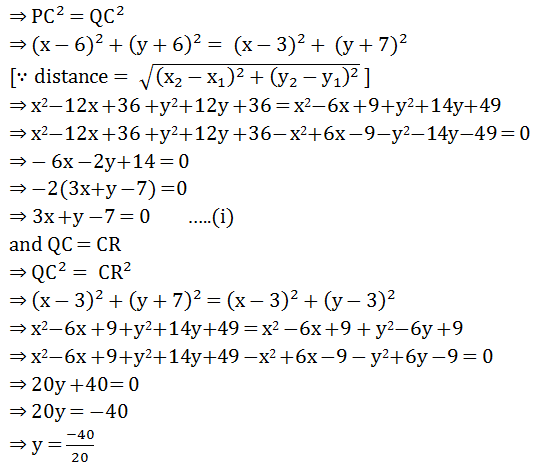
⇒ y = −2 ….(ii)
putting the value of y in eq. (i),
3x +y −7 = 0
⇒3x −2 −7 = 0
⇒ 3x−9 = 0
⇒ 3x = 9
⇒ x = 9/3
⇒ x = 3 .
Hence, centre (3 , −2).
4
Answer
Let PQRM be a square and let P(−1, 2)and R (3, 2) be the vertices. Let the coordinates of Q be (x, y).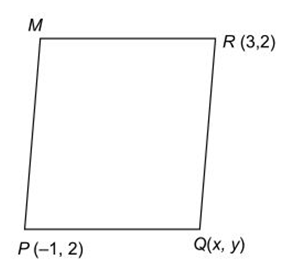
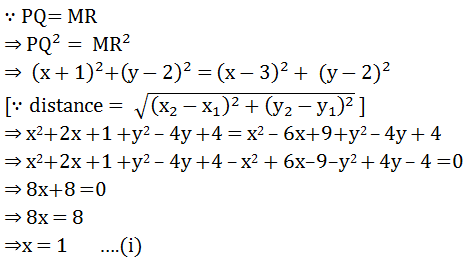

5

(i) Taking A as origin, find the coordinates of the vertices of the triangle.
(ii) What will be the coordinates of the vertices of ∆PQR, if C is the origin? Also, calculate the areas of the triangles in these cases. What do You observe?
Answer
(i) When Ais taken as origin, AD and AB as coordinate axes, i.e. , X-axis and Y-axis, respectively. Coordinates of P,Q and R are respectively (4, 6), (3, 2) and (6, 5) .
(ii) When C is taken as origin and CB as X-axis and CD as Y-axis.
∴ Coordinates of P, Q and R and are respectively(12, 2), (13, 6) and (10,3)
Areas of triangles according to both conditions
Condition (i)
When A is taken as origin and AD and AB as coordinates axes
6
Answer

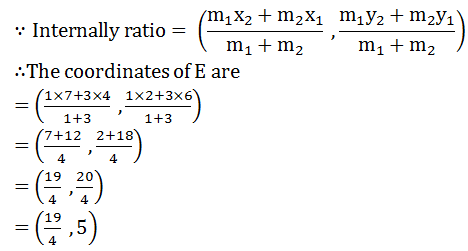
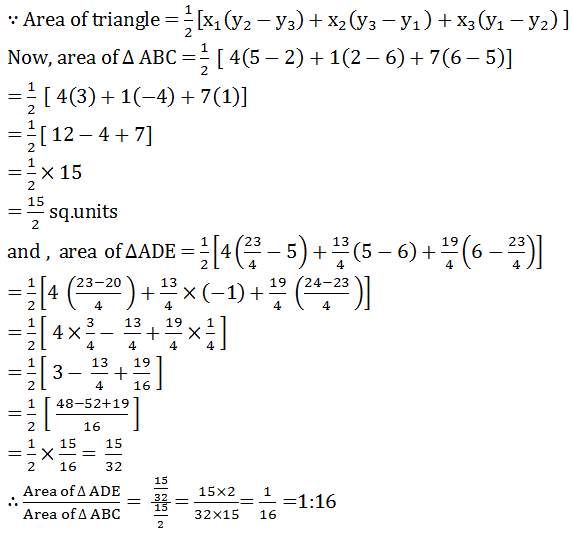
7
(i) The median from A meets BC at D. Find the coordinates of the point D.
(ii) Find the coordinates of the point P on AD such that AP :PD = 2:1.
(iii) Find the coordinates of points Q and R on medians BE and CF respectively,such that BQ:QE= 2:1and CR:RF = 2:1.
(iv) What do you observe?
(Note: The point which is common to all the three medians is called the centroid and this point divides each median in the ratio 2 : 1.)
(v) If A (X1 , Y1) , B(X2 , Y2) and C (X3 , Y3) are the vertices of ∆ABC, Find the
coordinates of the centroid of the triangle.
Answer
(i) Let A(4, 2), B(6, 5) and C(1, 4)be the vertices of ∆ABC.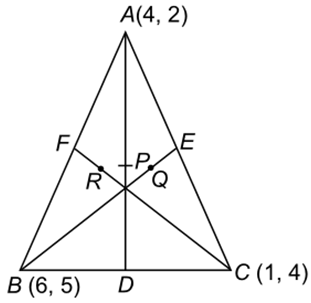
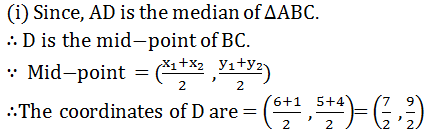


![]()
(v) Let A (X1 , Y1), B(X2, Y2) and C (X3, Y3) be the vertices of ∆ABC whose medians are AD, BE and CF respectively, then D ,E and F are respectively the mid-points of BC CA , and AB.
8
Answer