NCERT Solutions for Chapter 1 वास्तविक संख्याएँ Class 10 Maths
Book Solutions1
निम्नलिखित संख्याओं का म.स. ज्ञात करने के लिए यूक्लिड विभाजन एल्गोरिथ्म का प्रयोग कीजिए।
(i) 135 और 225 (ii) 196 और 38220 (iii) 867 और 255
Answer
Exercise 1.1
2
दर्शाइए कि कोई भी धनात्मक विषम पूर्णांक (6q + 1) या (6q + 3) या (6q + 5) के रूप का होता है, जब q कोई पूर्णाक है।
Answer
Exercise 1.1
3
किसी परेड में 616 सदस्यों वाली एक सेना (आर्मी) की टुकड़ी को 32 सदस्यों वाले एक आम बैंड के पीछे मार्च करना है। दोनों समूहों को समान संख्या वाले स्तम्भों में मार्च करना है। उन स्तम्भों की अधिकतम संख्या क्या है, जिसमें वे मार्च कर सकते हैं?
Answer
Exercise 1.1
4
यूक्लिड विभाजन प्रमेयिका का प्रयोग करके दर्शाइए कि किसी धनात्मक पूर्णाक का वर्ग किसी पूर्णांक m के लिए 3m या 3m + y के रूप में होता है।
[संकेत-यह मान लीजिए x कोई धनात्मक पूर्णांक है, तब यह 3q, 3g + 1 या 30 +2 के रूप में लिखा जा सकता है। इनमें से प्रत्येक का वर्ग कीजिए और दर्शाइए कि इन वर्गों को 3m या 3m+ 1 के रूप में लिखा जा सकता है।]
Answer
Exercise 1.1
5
यूक्लिड विभाजन प्रमेयिका का प्रयोग करके दर्शाइए कि किसी धनात्मक पूर्णाक का घन 9, 9m + 1 या 91 + 8 के रूप में होता है।
Answer
Exercise 1.1
1
निम्नलिखित संख्याओं को अभाज्य गुणनखंडों के गुणनफल के रूप में व्यक्त कीजिए।
(i) 140 (ii) 156 (iii) 3825 (iv) 5005 (v) 7429
Answer
Exercise 1.2
2
पूर्णाकों के निम्नलिखित युग्मों के म.स. और ल.स. ज्ञात कीजिए तथा इसकी जाँच कीजिए कि दो संख्याओं का गुणनफल = म.स.x ल.स. है।
(i) 26; और 91 (ii) 510 और 92 (iii) 336 और 54
Answer
Exercise 1.2
3
अभाज्य गुणनखंड विधि द्वारा निम्नलिखित पूर्णाकों के म.स. और ल.स. ज्ञात कीजिए।
(i) 12,15 तथा 21 (ii) 17, 23 तथा 29 (iii) 8, 9 तथा 25
Answer
Exercise 1.2
4
म.स.(306, 657) = 9, दिया है। ल.स.(306, 657) ज्ञात कीजिए।
Answer
Exercise 1.2
5
जाँच कीजिए कि क्या किसी प्राकृत संख्या n के लिए, संख्या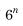 
अंक O पर समाप्त हो सकती है?
अंक O पर समाप्त हो सकती है? Answer
हल यदि संख्या 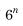, शून्य के साथ समाप्त होती है। तब, यह 5 से विभाज्य होगी अर्थात् के अभाज्य गुणनखंडों में 5 अभाज्य संख्या है। यह सम्भव नहीं है क्योंकि 6" के अभाज्य गुणनखंडों में केवल 2 और 3 हैं। और अंकगणित के अद्वितीय मूलभूत प्रमेय आश्वसित करते हैं कि के अन्य गुणनखंड नहीं है।
, शून्य के साथ समाप्त होती है। तब, यह 5 से विभाज्य होगी अर्थात् 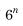के अभाज्य गुणनखंडों में 5 अभाज्य संख्या है। यह सम्भव नहीं है क्योंकि 6" के अभाज्य गुणनखंडों में केवल 2 और 3 हैं। और अंकगणित के अद्वितीय मूलभूत प्रमेय आश्वसित करते हैं कि 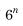के अन्य गुणनखंड नहीं है। अतः प्राकृत संख्या १ का कोई भी मान ऐसा नहीं है जिसका इकाई अंक शून्य हो।
Exercise 1.2
6
व्याख्या कीजिए कि 7x11x13 + 13 और 7x6x5x4x3x2x1+ 5 भाज्य संख्याएँ क्यों हैं?
Answer
Exercise 1.2
7
किसी खेल के मैदान के चारों ओर एक वृत्ताकार पथ है। इस मैदान का एक चक्कर लगाने में सोनिया को 18 मिनट लगते हैं, जबकि इसी मैदान का एक चक्कर लगाने में रवि को 12 मिनट लगते हैं। मान लीजिए वे दोनों एक ही स्थान और एक ही समय पर चलना प्रारम्भ करके एक ही दिशा में चलते हैं। कितने समय बाद वे पुनः प्रारंभिक स्थान पर मिलेंगे?
Answer
Exercise 1.2
1
सिद्ध कीजिए कि ✓5 एक अपरिमेय संख्या है।
Answer
Exercise 1.3
2
सिद्ध कीजिए कि 3 + 2✓5 एक अपरिमेय संख्या है।
Answer
Exercise 1.3
3
सिद्ध कीजिए कि निम्नलिखित संख्याएँ अपरिमेय है।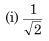
(ii) 7✓5
(iii) 6 + ✓2
Answer
Exercise 1.3
1
लंबी विभाजन प्रक्रिया किए बिना बताइए कि निम्नलिखित परिमेय संख्याओं के दशमलव प्रसार सांत हैं या असांत आवर्ती हैं?
Answer
Exercise 1.4
2
ऊपर दिए गए प्रश्न में उन परिमेय संख्याओं के दशमलव प्रसारों को लिखिए जो सांत है।
Answer
Exercise 1.4
3
ऊपर दिए गए प्रश्न में उन परिमेय संख्याओं के दशमलव प्रसारों को लिखिए जो सांत है। कुछ वास्तविक संख्याओं के दशमलव प्रसार नीचे दर्शाए गए हैं। प्रत्येक स्थिति के लिए निर्धारित कीजिए कि यह संख्या परिमेय संख्या है या नहीं। यदि यह परिमेय संख्या है और p/q के रूप की है, तो q के अभाज्य गुणनखंडों के बारे में आप क्या कह सकते हैं?
(i) 43.123456789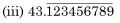
(ii) 0.120120012000120000......
Answer
Exercise 1.4