Triangles

Class 9 > Math > NCERT > Triangles

NCERT Solutions for Chapter 7 Triangles Class 9 Maths

Book Solutions

1

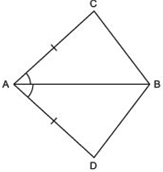
In quadrilateral ACBD, AC = AD and AB bisects ∠A (see figure). Show that ΔABC ≅ ΔABD. What can you say about BC and BD?

Answer

In quadrilateral ABCD we have AC = AD
and AB being the bisector of ∠A.
Now, in ΔABC and ΔABD,

AC = AD  [Given]
AB = AB  [Common]
∠CAB = ∠DAB  [∵ AB bisects ∠ CAD]
∴ Using SAS criteria, we have ΔABC ≌ ΔABD.
∵ Corresponding parts of congruent triangles (c.p.c.t) are equal.
∴ BC = BD.
Exercise 7.1 Page Number 118

2

ABCD is a quadrilateral in which AD = BC and ∠DAB = ∠CBA (see Figure). Prove that

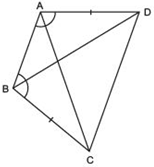
(i) ΔABD ≅ ΔBAC
(ii) BD = AC
(iii) ΔABD ≅ ΔBAC.

Answer

In quadrilateral ABCD, we have AD = BC and ∠DAB = ∠CBA.
In ΔABD and ΔBAC,

(i) AD = BC  [Given]
AB = BA   [Common]
∠DAB = ∠CBA   [Given]
∴ Using SAS criteria, we have ΔABD ≌ ΔBAC


(ii) ∵ ΔABD ≌ ΔBAC
∴ Their corresponding parts are equal.
⇒ BD = AC


(iii) Since ΔABD ≌ ΔBAC
∴ Their corresponding parts are equal.
⇒ ΔABD ≅ ΔBAC.

Exercise 7.1 Page Number 119

3

AD and BC are equal perpendiculars to a line segment AB (see figure). Show that CD bisects AB.

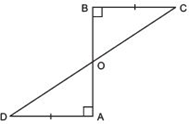
Answer

We have ∠ABC = 90° and ∠BAD = 90°
Also AB and CD intersect at O.
∴ Vertically opposite angles are equal.
Now, in ΔOBC and ΔOAD, we have

∠ABC = ∠BAD  [each = 90°]
BC = AD  [Given]
∠BOC = ∠AOD  [vertically opposite angles]
∴ Using ASA criteria, we have ΔOBC ≌ ΔOAD
⇒ OB = OA  [c.p.c.t.]
i.e. O is the mid-point of AB Thus, CD bisects AB.
Exercise 7.1 Page Number 119

4

l and m are two parallel lines intersected by another pair of parallel lines p and q (see figure). Show that ΔABC ≅ ΔCDA.

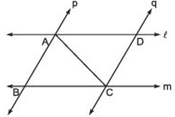
Answer

∵ ℓ || m and AC is a transversal,
∴ ∠BAC = ∠DCA   [Alternate interior angles]
Also p || q and AC is a transversal,
∴ ∠BCA = ∠DAC  [Alternate interior angles]
Now, in ΔABC and ΔCDA,
∠BAC = ∠DCA  [Proved]
∠BCA = ∠DAC   [Proved]
CA = AC  [Common]
∴ Using ASA criteria, we have ΔABC ≌ ΔCDA
Exercise 7.1 Page Number 119

5

Line l is the bisector of an angle A and B is any point on l. BP and BQ are perpendiculars from B to the arms of ∠A (see Figure). Show that:
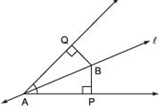
(i) ΔAPB ≅ ΔAQB
(ii) BP = BQ or B is equidistant from the arms of ∠ A.

Answer

(i) We have, ℓ as the bisector of QAP.
∴ ∠QAB = ∠PAB
∠Q= ∠P   [each = 90°]
⇒ ∠ABQ = ∠ABP  [Two angles of trinagles are equal then third will also be equal]
Now, in ΔAPB and ΔAQB, we have
AB = AB  [common]
∠ABP = ∠ABQ  [proved]
∠PAB = ∠QAB  [proved]
∴ Using SAS criteria, we have ΔAPB ≌ ΔAQB


(ii) Since ΔAPB ≌ ΔAQB
∴ Their corresponding angles are equal.
⇒ BP = BQ
i.e. [Perpendicular distance of B from AP] = [Perpendicular distance of B from AQ]
Thus, the point B is equidistant from the arms of ∠A.

Exercise 7.1 Page Number 119

6

In the figure, AC = AE, AB = AD and ∠BAD = ∠EAC. Show that BC = DE.

Answer

We have ∠BAD = ∠EAC
Adding ∠DAC on both sides, we have
∠BAD + ∠DAC = ∠EAC + ∠DAC
⇒ ∠BAC = ∠DAE
Now, in ΔABC and ΔADE, we have
∠BAC = ∠DAE   [Proved]
AB = AD  [Given]
AC = AE   [Given]
∴ ΔABC ≌ ΔADE   [Using SAS criteria]
Since ΔABC ≌ ΔADE, therefore, their corresponding parts are equal.
⇒ BC = DE.
Exercise 7.1 Page Number 120

7

AB is a line segment and P is its mid-point. D and E are points on the same side of AB such that ∠BAD = ∠ABE and ∠EPA = ∠DPB (see figure). Show that
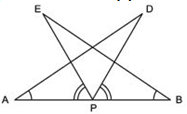
(i) ΔDAP ≅ ΔEBP
(ii) AD = BE

Answer

We have, P is the mid-point of AB.
∴ AP = BP
∠EPA = ∠DPB   [Given]
Adding ∠EPD on both sides, we get
∠EPA + ∠EPD = ∠DPB + ∠EPD
⇒ APD = ∠BPE


(i) Now, in ΔDAP ≌ ΔEBP, we have
AP = BP  [Proved]
∠PAD = ∠PBE    [∵ It is given that ∠BAD = ∠ABE]
∠DPA = ∠EPB    [Proved]
∴ Using ASA criteria, we have
ΔDAP ≌ΔEBP


(ii) Since, ΔDAP ≌ΔEBP
∴ Their corresponding parts are equal. ⇒ AD = BE.

Exercise 7.1 Page Number 120

8

In right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see figure). Show that

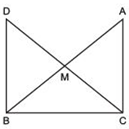
(i) ΔAMC ≅ΔBMD
(ii) ∠DBC is a right angle.
(iii) ΔDBC ≅ ΔACB
(iv) CM = (1/2)AB

Answer

∵ M is the mid-point of AB.
∴ BM = AM    [Given]


(i) In ΔAMC and ΔBMD, we have CM = DM   [Given]
AM = BM   [Proved]
∠AMC = ∠BMD   [Vertically opposite angles]
∴ ΔAMC ≌ ΔBMD    (SAS criteria)


(ii) ∵ ΔAMC ≌ ΔBMD
∴ Their corresponding parts are equal.
⇒ ∠MAC = ∠MBD But they form a pair of alternate interior angles.
∴ AC || DB
Now, BC is a transversal which intersecting parallel lines AC and DB,
∴ ∠BCA + ∠DBC = 180°
But ∠BCA = 90  [∵ ΔABC is right angled at C]
∴ 90° + ∠DBC = 180°
or ∠DBC = 180° ∠ 90° = 90°
Thus, ∠DBC = 90°


(iii) Again, ΔAMC ≌ ΔBMD   [Proved]
∴ AC = BD    [c.p.c.t]
Now, in ΔDBC and ΔACB, we have
∠DBC = ∠ACB     [Each = 90°]
BD = CA  [Proved]
BC = CB   [Common]
∴ Using SAS criteria, we have ΔDBC ≌ ΔACB


(iv) ∵ ΔDBC ≌ ΔACB
∴ Their corresponding parts are equal.
⇒ DC = AB
But DM = CM    [Given]
∴ CM = (1/2) DC = (1/2) AB
⇒ CM = (1/2) AB

Exercise 7.1 Page Number 120

1

In an isosceles triangle ABC, with AB = AC, the bisectors of B and ∠C intersect each other at O. Join A to O. Show that:
(i) OB = OC
(ii) AO bisects ∠A

Answer

(i) In ΔABC, we have AB = AC  [Given]
∴ ∠C= ∠B   [Angle opposite to equal sides are equal]

⇒ (1/2)∠C= (1/2)∠B
or ∠OCB = ∠OBC
⇒ OB = OC   [Sides opposite to equal angles are equal]


(ii) In ΔABO and ΔACO, we have
AB = AC   [Given]
OB = OC    [Proved]
∠OBA = ∠OCA    [(1/2)∠B = (1/2)∠C ]
∴ Using SAS criteria,
ΔABO ≌ ΔACO
⇒ ∠OAB = ∠OAC  [c.p.c.t.]
⇒ AO bisects ∠A.

Exercise 7.2 Page Number 123

2

In ΔABC, AD is the perpendicular bisector of BC (see figure). Show that ΔABC is an isosceles triangle in which AB = AC.

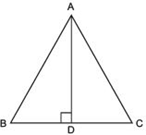
Answer

∵ AD is bisector of BC.
∴ BD = CD
Now, in ΔABD and ΔACD, we have:
AD = AD  [Common]
∠ADB = ∠ADC = 90°   [∵ AD ⊥ BC]
BD = CD  [Proved]
∴ ΔABD ≌ ΔACD   [SAS criteria]

∴ Their corresponding parts are equal.
⇒ AB = AC Thus, ΔABC is an isosceles triangle.
Exercise 7.2 Page Number 123

3

ABC is an isosceles triangle in which altitudes BE and CF are drawn to equal sides AC and AB respectively (see Figure) Show that these altitudes are equal.
OR
ABC is an isosceles triangle with AB = AC. Prove that the altitudes BE and CF of the triangle are equal.

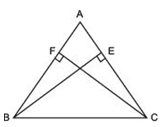
Answer

ΔABC is an isosceles triangle.
∴ AB = AC
⇒ ∠ACB = ∠ABC  [∵ Angles opposite to equal sides are equal]
Now, in ΔBEC and ΔCFB, we have
∠EBC = ∠FCB   [Proved]
BC = CB  [Common]
and ∠BEC = ∠CFB   [Each = 90°]
∴ ΔBEC ≌ ΔCFB   [Using ASA criteria]
⇒ Their corresponding parts are equal. i.e. BE = CF
Exercise 7.2 Page Number 124

4

ABC is a triangle is which altitudes BE and CF to sides AC and AB are equal (see figure). Show that
(i) ΔABE ≌ ΔACF
(ii) AB = AC, i.e. ABC is an isosceles triangle.

Answer

(i) In ΔABE and ΔACF, we have

∠AEB = ∠AFC  [each = 90° ∵ BE ⊥ AC and CF ⊥ AB]
∠A= ∠A  [Common]
BE = CF  [Given]
∴ ΔABE ≌ ΔACF  [Using AAS criterion]


(ii) Since, ΔABE ≌ ΔACF
∴ Their corresponding parts are equal.
⇒ AB = AC 

Exercise 7.2 Page Number 124

5

ABC and DBC are two isosceles triangles on the same base BC (see figure). Show that ∠ABD≌ ∠ACD.

Answer

In ΔABC, we have AB = AC   [∵DABC is an isosceles triangle]

But angles opposite to equal sides are equal.
∴ ∠ABC = ∠ACB   ...(1)
Again, in ΔBDC, we have BD = CD 

[∵ΔBDC is an isosceles triangle.]
∴ ∠CBD = ∠BCD   ...(2) 

[Angles opposite to equal sides are equal]

Adding (1) and (2), we have
∠ABC + ∠CBD = ∠ACB + ∠BCD
⇒ ∠ABD = ∠ACD

Exercise 7.2 Page Number 124

6

ΔABC is an isosceles triangle in which AB = AC. Side BA is produced to D such that AD = AB (see figure). Show that ∠BCD is a right angle.

Answer

∵ In ΔABC, AB = AC  [Given]   …(1)
AB = AD  [Given]   …(2)
From (1) and (2), we have AC = AD

Now, in ΔABC, we have ∠B + ∠ACB + ∠BAC = 180°
⇒ 2∠ACB + ∠BAC = 180°  …(3)

[∵ ∠B = ∠ACB (Angles opposite to equal sides)]
In ΔACD, ∠D + ∠ACD + ∠CAD = 180°
⇒ 2∠ACD + ∠CAD = 180°   ...(4) 

[∵∠D = ∠ACD (angles opposite to equal sides)]
Adding (3) and (4), we have
2∠ACB + ∠BAC + 2∠ACD + ∠CAD = 180° + 180°
⇒ 2[∠ACB + ∠ACD] + [∠BAC + ∠CAD] = 360°
⇒ 2[∠BCD] + [180°] = 360°   [∠BAC and ∠CAD form a linear pair]
⇒ 2∠BCD = 360°
⇒ ∠BCD = (180°/2)= 90°
Thus,  ∠BCD = 90°.

Exercise 7.2 Page Number 124

7

ABC is a right angled triangle in which ∠A = 90° and AB = AC. Find ∠B and ∠C.

Answer

In ΔABC, we have AB = AC  [Given]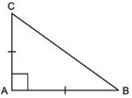

∴ Their opposite angles are equal.
⇒ ∠ACB = ∠ABC
Now, ∠A + ∠B + ∠C = 180°
⇒ 90° + ∠B + ∠C = 180°  [∵ ∠A = 90° (Given)]
⇒ ∠B + ∠C = 180°
But ∠ABC = ∠ACB,
i.e. ∠B = ∠C
∴ ∠B= ∠C = (90°/2) = 45°
Thus, ∠B = 45° and ∠C = 45°
Exercise 7.2 Page Number 124

8

Show that the angles of an equilateral triangle are 60° each.

Answer

In ΔABC, we have
AB = BC = CA   [∵ ABC is an equilateral triangle]
∴ AB = BC ⇒ ∠A = ∠C   …(1) 

[∵ Angle opposite to equal sides are equal.]
Similarly, AC = BC ⇒ ∠A = ∠B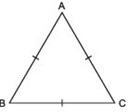

From (1) and (2), we have ∠A= ∠B = ∠C
Let ∠A= ∠B = ∠C = x
Since, ∠A + ∠B + ∠C = 180°
∴ x + x + x = 180°
⇒ 3x = 180° or x =(180°/3) = 60°
∴ ∠A= ∠B = ∠C = 60°
Thus, the angles of an equilateral triangle are 60° each.

Exercise 7.2 Page Number 124

1

ΔABC and ΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see figure).
If AD is extended to intersect BC at P, show that
(i) ΔABD ≌ ΔACD
(ii) ΔABP ≌ ΔACP
(iii) AP bisects ∠ A as well as ∠ D.
(iv) AP is the perpendicular bisector of BC.

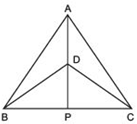
Answer

(i) In ΔABD and ΔACD, we have
AB = AC   [Given]
AD = AD   [Common]
BD = CD   [Given]
∴ ΔABD ≌ ΔACD   [SSS Criteria]


(ii) In ΔABP and ΔACP, we have
AB = AC    [Given]
∴ AB = AC
⇒ ∠B = ∠C   [∵Angle opposite to equal sides are equal]
AP = AP    [Common]
∴ ΔABP ≌ ΔACP   [SAS Criteria]


(iii) Since, ΔABP ≌ ΔACP
∴ Their corresponding parts are congruent.
⇒ ∠BAP = ∠CAP
∴ AP is the bisector of ∠A   ...(1)
Again, in ΔBDP and ΔCDP, we have
BD = CD   [Given]
∠DBP = ∠CDP    [Angles opposite to equal sides]
DP = DP   [Common]
⇒ ∠BDP ≌ ∠CDP
∴ ∠BDP = ∠CDP   [c.p.c.t.]
⇒ DP (or AP) is the bisector of ∠D   ...(2)
From (1) and (2), AP is the bisector of ∠A as well as ∠D.


(iv) ∵ ΔABP ≌ ΔACP
∴ Their corresponding parts are equal.
⇒ ∠APB = ∠APC
But ∠APB + ∠APC = 180º   [Linear pair]
∴ ∠APB = ∠APC = 90º
⇒  AP ⊥ BC
⇒ AP is the perpendicular bisector of BC

Exercise 7.3 Page Number 128

2

AD is an altitude of an isosceles triangle ABC in which AB = AC. Show that
(i) AD bisects BC
(ii) AD bisects ∠A

Answer

(i) In ΔABD and ΔACD, we have
AB = AC   [Given]
∠B= ∠C   [Angles opposite to equal sides]
AD = AD    [Common]

∴ ΔABD ≌ ΔACD
⇒ Their corresponding parts are equal.
∴ BD = CD
⇒ D is the mid-point of BC or AD bisects BC.


(ii) Since, ΔABD ≌ ΔACD,
∴ Their corresponding parts are congruent.
⇒ ∠BAD = ∠CAD
⇒ AD bisects ∠A.

Exercise 7.3 Page Number 128

3

Two sides AB and BC and median AM of one triangle ABC are respectively equal to sides PQ and QR and median PN of ΔPQR (see figure). Show that

(i) ΔABM ≌ ΔPQN
(ii) ΔABC ≌ ΔPQR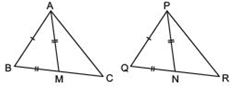

Answer

In ΔABC, AM is a median   [Given].
∴ BM = (1/2)BC  …(1)
In ΔPQR, PN is a median.
∴ QN = (1/2)QR  …(2)
∵ BC = QR   [Given]
∴ (1/2)BC = (1/2)QR
⇒ BM = QN   [From (1) and (2)]


(i) In ΔABM and ΔPQN, we have
∵ AB = PQ   [Given]
AM = PN    [Given]
BM = QN   [Proved]
∴ ΔABM ≌ ΔPQN   [SSS criteria]


(ii) ∵ ΔABM ≌ ΔPQN
∴ Their corresponding parts are congruent.
⇒ ∠B= ∠Q
Now, in ΔABC and ΔPQR, we have
∠B= ∠Q   [Proved]
AB = PQ  [Given]
BC = QR   [Given]
∴ ΔABC ≌ ΔPQR

Exercise 7.3 Page Number 128

4

BE and CF are two equal altitudes of a triangle ABC. Using RHS congruence rule, prove that the triangle ABC is isosceles.

Answer

∵ BE ⊥ AC   [Given]
∴ ΔBEC is a right triangle such that ∠BEC = 90º
Similarly, ∠CFB = 90º
Now, in right ΔBEC and right ΔCFB, we have

BE = CF   [Given]
BC = CB   [common]
∴ Using RHS criteria,
ΔBEC ≌ ΔCFB
∴ Their corresponding parts are equal.
⇒ ∠BCE = ∠CBF or ∠BCA = ∠CBA
Now, in ΔABC, ∠BCA = ∠CBA
∴ Their opposite sides are equal.
⇒ AB = AC
∴ ΔABC is an isosceles triangle.
Exercise 7.3 Page Number 128

5

ABC is an isosceles triangle with AB = AC. Draw AP ⊥ BC to show that ∠B = ∠C.

Answer

We have AP ⊥ BC  [Given]
∴ ∠APB = 90º and APC = 90º
In ΔABP and ΔACP, we have

∠APB = ∠APC  [each = 90º]
AB = AC  [Given]
AP = AP   [common]
∴ Using RHS criteria,
ΔABP ≌ ΔACP
∴ Their corresponding parts are congruent.
⇒ ∠B= ∠C
Exercise 7.3 Page Number 128

1

Show that in a right angled triangle, the hypotenuse is the longest side.

Answer

Let us consider ΔABC such that ∠B = 90º
∴ ∠A + ∠B + ∠C = 180º
∴ [∠A + ∠C] + ∠B = 180º
⇒ ∠A + ∠C = 90º
⇒ ∠A + ∠C= ∠B
∴ ∠B > ∠A and ∠B > ∠C

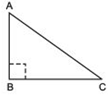
⇒ Side opposite to ∠B is longer than the side opposite to ∠A.
i.e. AC > BC   ...(1)
Similarly, AC > AB    ...(2)
From (1) and (2), we get AC is the longest side.
But AC is the hypotenuse of the triangle.
Thus, hypotenuse is the longest side.
Exercise 7.4 Page Number 132

2

In the adjoining figure, sides AB and AC of ΔABC are extended to points P and Q respectively. Also, ∠PBC < ∠QCB. Show that AC > AB.

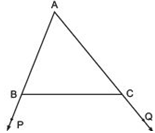
Answer

∠ABC + ∠PBC = 180º   [Linear pair]

and ∠ACB + ∠QCB = 180º   [Linear pair]
∴ ∠ABC + ∠PBC = ∠ACB + ∠QCB
But ∠PBC < ∠QCB   [Given]
∴ ∠ABC > ∠ACB
⇒ [The side opposite to ∠ABC] > [The side opposite to ∠ACB]
⇒ AC > AB
Exercise 7.4 Page Number 132

3

In the figure, ∠B < ∠A and ∠C < ∠D. Show that AD > BC.

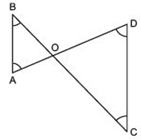
Answer

∵ ∠B< ∠A   [Given]
⇒ ∠A> ∠B
∴ OB > OA  ...(1)
[Side opposite to greater angle is longer]

Similarly, OC > OD   ...(2)
From (1) and (2), we have
[OB + OC] > [OA + OD]
⇒ BC > AD or AD < BC
Exercise 7.4 Page Number 132

4

AB and CD are respectively the smallest and longest sides of a quadrilateral ABCD (see figure). Show that ∠A > ∠C and ∠B > ∠D.

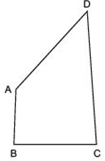
Answer

Let us join AC.

Now, in ΔABC, AB < BC  [∵ AB is the smallest side of quadrilateral ABCD]
⇒ BC > AB
∴ [Angle opposite to BC] < [Angle opposite to AB]
⇒ ∠BAC > ∠BCA   ...(1)
Again, in ΔACD,
CD > AD   [∵ CD is the longest side of the quadrilateral ABCD]
∴ [Angle opposite to CD] > [Angle opposite to AD]
⇒ ∠CAD > ∠ACD  ...(2)

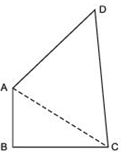
Adding (1) and (2), we get
[∠BAC + CAD] > [∠BCA + ∠ACD]
⇒ ∠A> ∠C
Similarly, by joining BD, we have ∠B> ∠D
Exercise 7.4 Page Number 132

5

In the figure, PR > PQ and PS bisects ∠QPR. Prove that ∠PSR > ∠PSQ.

Answer

In ΔPQR, PS bisects ∠QPR  [Given]
∴ ∠QPS = ∠RPS
∵ PR > PQ  [Given]

∴ [Angle opposite to PR] > [Angle opposite to PQ]
⇒ ∠PQS > ∠PRS
⇒ [∠PQS + ∠QPS] > [∠PRS + ∠RPS]  ...(1)
[∵ ∠QPS = ∠RPS]
∵ Exterior ∠PSR = [∠PQS + ∠QPS]
[∵ An exterior angle is equal to the sum of interior opposite angles]
and  Exterior ∠PSQ = [∠PRS + ∠RPS]
Now, from (1), we have ∠PSR > ∠PSQ
Exercise 7.4 Page Number 132

6

Show that of all line segments drawn from a given point not on it, the perpendicular line segment is the shortest.

Answer

Let us consider the ΔPMN such that ∠M = 90º
Since, ∠M + ∠N + ∠P = 180º

[Sum of angles of a triangle] ∵
∠M = 90º [∵ PM ⊥ ℓ]
⇒ ∠N< ∠M ⇒ PM < PN   ...(1)
Similarly, PM < PN1   ...(2)
PM < PN2    ...(3)
From (1), (2) and (3), we have PM is the smallest line segment drawn from P on the line l.
Thus, the perpendicular segment is the shortest line segment drawn on a line from a point not on it.
Exercise 7.4 Page Number 133

1

ABC is a triangle. Locate a point in the interior of ΔABC which is equidistant from all the vertices of ΔABC.

Answer

Let us consider a ΔABC.
Draw ‘l’ the perpendicular bisector of AB.
Draw ‘m’ the perpendicular bisector of BC.
Let the two perpendicular bisectors ‘l’ and ‘m’ meet at O. ‘O’ is the required point which is equidistant from A, B and C.

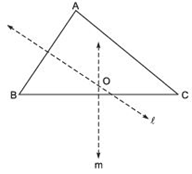
Note: If we draw a circle with centre ‘O’ and radius OB or OC, then it will pass through A, B and C.
Exercise 7.5 Page Number 133

2

In a triangle, locate a point in its interior which is equidistant from all the sides of the triangle.

Answer

Let us consider a ΔABC.
Draw ‘l’ the bisector of ∠B.
Draw ‘m’ the bisector of ∠C.
Let the two bisectors l and m meet at O. Thus, ‘O’ is the required point which is equidistant from the sides of ΔABC.

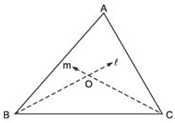
required point which is equidistant from the sides of ΔABC.
Note: If we draw OM ⊥ BC and draw a circle with O as centre and OM as radius, then the circle will touch the sides of the triangle.
Exercise 7.5 Page Number 133

3

In a huge park, people are concentrated at three points (see figure): A : where there are different slides and swings form children,

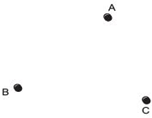
B : near which a man-made lake is situated, C: which is near to a large parking and exit.
Where should an ice cream parlour be set up so that maximum number of persons can approach it?
Hint: The parlour should be equidistant from A, B and C.

Answer

Let us join A and B, and draw ‘l’ the perpendicular bisector of AB.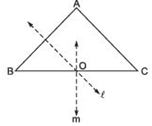

Now, join B and C, and draw ‘m’ the perpendicular bisector of BC. Let the perpendicular bisectors ‘l’ and ‘m’ meet at ‘O’. The point ‘O’ is the required point where the ice cream parlour be set up.
Note: If we join ‘A’ and ‘C’, and draw the perpendicular bisectors, then it will also meet (or pass through) the point O.
Exercise 7.5 Page Number 133

4

Complete the hexagonal and star shaped Rangolies [see Fig. (i) and (ii)] by filling them with as many equilateral triangles of side 1 cm as you can. Count the number of triangles in each case. Which has more triangles?

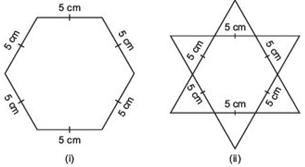
Answer

It is an activity. We get the 150 equilateral triangles in the figure
(i) 300 equilateral triangles in the figure
(ii) ∴ The figure
(ii) has more triangles.
Exercise 7.5 Page Number 133

Ads