NCERT Solutions for Chapter 14 Statistics Class 10 Maths
Book Solutions1
A survey was conducted by a group of students as a part of their environment awareness programme, in which they collected the following data regarding the number of plants in 20 houses in a locality. Find the mean number of plants per house.
|
Number of Plants |
0-2 |
2-4 |
4-6 |
6-8 |
8-10 |
10-12 |
12-14 |
|
Number of Houses |
1 |
2 |
1 |
5 |
6 |
2 |
3 |
Which method did you use for finding the mean, and why?
Answer
|
No. of plants |
No. of houses (fi) |
Mid-point (xi) |
fixi |
|
0-2 |
1 |
1 |
1 |
|
2-4 |
2 |
3 |
6 |
|
4-6 |
1 |
5 |
5 |
|
6-8 |
5 |
7 |
35 |
|
8-10 |
6 |
9 |
54 |
|
10-12 |
2 |
11 |
22 |
|
12-14 |
3 |
13 |
39 |
|
Sum fi = 20 |
Sum fixi = 162 |
![]()
We would use direct method because the numerical value of fi and xi are small.
2
Consider the following distribution of daily wages of 50 workers of a factory.
|
Daily wages (in Rs.) |
100-120 |
120-140 |
140-160 |
160-180 |
180-200 |
|
Number of workers |
12 |
14 |
8 |
6 |
10 |
Find the mean daily wages of the workers of the factory by using an appropriate method.
Answer
Here, the value of mid-point (xi) is very large, so assumed mean A = 150 and class interval is h = 20.![]()
|
Daily wages |
Number of workers |
Mid-point (xi) |
ui = (xi-150)/20 |
fiui |
|
100-120 |
12 |
110 |
-2 |
-24 |
|
120-140 |
14 |
130 |
-1 |
-14 |
|
140-160 |
8 |
150 |
0 |
0 |
|
160-180 |
6 |
170 |
1 |
6 |
|
180-200 |
10 |
190 |
2 |
20 |
|
Total |
Sum fi = 50 |
Sum fiui = -12 |
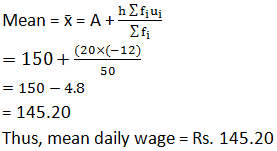
3
The following distribution shows the daily pocket allowance of children of a locality. The mean pocket allowance is Rs 18. Find the missing frequency f.

Answer
Here, the value of mid-point (xi) mean x̄ = 18
|
Class interval |
Number of children (fi) |
Mid-point (xi) |
fixi |
|
11-13 |
7 |
12 |
84 |
|
13-15 |
6 |
14 |
84 |
|
15-17 |
9 |
16 |
144 |
|
17-19 |
13 |
18 = A |
234 |
|
19-21 |
f |
20 |
20f |
|
21-23 |
5 |
22 |
110 |
|
23-25 |
4 |
24 |
96 |
|
Total |
fi = 44+f |
Sum fixi = 752+20f |
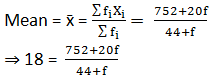
⇒ 18(44+f) = (752+20f)
⇒ 792+18f = 752+20f
⇒ 792+18f = 752+20f
⇒ 792 - 752 = 20f - 18f
⇒ 40 = 2f
⇒ f = 20
4
Thirty women were examined in a hospital by a doctor and the number of heart beats per minute were recorded and summarised as follows. Find the mean heart beats per minute for these women, choosing a suitable method.

Answer
|
Class Interval |
Number of women (fi) |
Mid-point (xi) |
ui =(xi-75.5)/h |
fiui |
|
65-68 |
2 |
66.5 |
-3 |
-6 |
|
68-71 |
4 |
69.5 |
-2 |
-8 |
|
71-74 |
3 |
72.5 |
-1 |
-3 |
|
74-77 |
8 |
75.5 |
0 |
0 |
|
77-80 |
7 |
78.5 |
1 |
7 |
|
80-83 |
4 |
81.5 |
3 |
8 |
|
83-86 |
2 |
84.5 |
3 |
6 |
|
Sum fi= 30 |
Sum fiui = 4 |

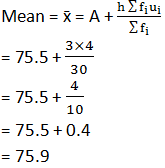
The mean heart beats per minute for these women is 75.9
5

Find the mean number of mangoes kept in a packing box. Which method of finding the mean did you choose?
Answer
Since, the given data is not continuous so we add 0.5 to the upper limit and subtract 0.45 from the lower limit.
Here, assumed mean (A) = 57
Class size (h) = 3
|
Class Interval |
Number of boxes (fi) |
Mid-point (xi) |
di = xi - A |
fidi |
|
49.5-52.5 |
15 |
51 |
-6 |
90 |
|
52.5-55.5 |
110 |
54 |
-3 |
-330 |
|
55.5-58.5 |
135 |
57 = A |
0 |
0 |
|
58.5-61.5 |
115 |
60 |
3 |
345 |
|
61.5-64.5 |
25 |
63 |
6 |
150 |
|
Sum fi = 400 |
Sum fidi = 75 |
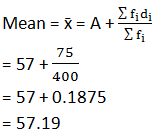
6
The table below shows the daily expenditure on food of 25 households in a locality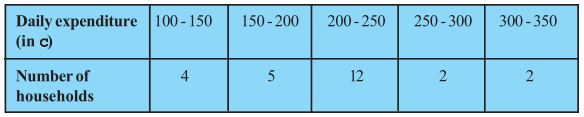
Find the mean daily expenditure on food by a suitable method.
Answer
Here, assumed mean (A) = 225
Class Interval | Number of households (fi) | Mid-point (xi) | di = xi - A | fidi |
100-150 | 4 | 125 | -100 | -400 |
150-200 | 5 | 175 | -50 | -250 |
200-250 | 12 | 225 | 0 | 0 |
250-300 | 2 | 275 | 50 | 100 |
300-350 | 2 | 325 | 100 | 200 |
Sum fi = 25 | Sum fidi = -350 |

= 225 - 14
= 211
The mean daily expenditure on food is 211.
7
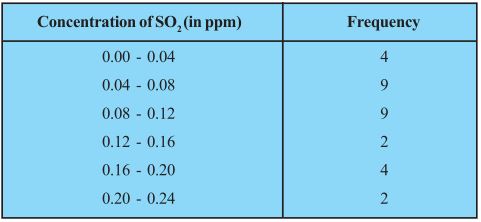
Find the mean concentration of SO2 in the air.
Answer
|
Concentration of SO2 (in ppm) |
Frequency (fi) |
Mid-point (xi) |
fixi |
|
0.00-0.04 |
4 |
0.02 |
0.08 |
|
0.04-0.08 |
9 |
0.06 |
0.54 |
|
0.08-0.12 |
9 |
0.10 |
0.90 |
|
0.12-0.16 |
2 |
0.14 |
0.28 |
|
0.16-0.20 |
4 |
0.18 |
0.72 |
|
0.20-0.24 |
2 |
0.20 |
0.40 |
|
Total |
Sum fi = 30 |
Sum (fixi) = 2.96 |
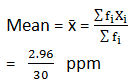
8
A class teacher has the following absentee record of 40 students of a class for the whole term. Find the mean number of days a student was absent.
|
Number of days |
0-6 |
6-10 |
10-14 |
14-20 |
20-28 |
28-38 |
38-40 |
|
Number of students |
11 |
10 |
7 |
4 |
4 |
3 |
1 |
Answer
|
Class interval |
Frequency (fi) |
Mid-point (xi) |
fixi |
|
0-6 |
11 |
3 |
33 |
|
6-10 |
10 |
8 |
80 |
|
10-14 |
7 |
12 |
84 |
|
14-20 |
4 |
17 |
68 |
|
20-28 |
4 |
24 |
96 |
|
28-38 |
3 |
33 |
99 |
|
38-40 |
1 |
39 |
39 |
|
Sum fi = 40 |
Sum fixi = 499 |
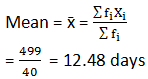
9
The following table gives the literacy rate (in percentage) of 35 cities. Find the mean
literacy rate.
|
Literacy rate (in %) |
45-55 |
55-65 |
65-75 |
75-85 |
85-98 |
|
Number of cities |
3 |
10 |
11 |
8 |
3 |
Answer
|
Class Interval |
Frequency (fi) |
(xi) |
di = xi - a |
ui = |
fiui |
|
45-55 |
3 |
50 |
-20 |
-2 |
-6 |
|
55-65 |
10 |
60 |
-10 |
-1 |
-10 |
|
65-75 |
11 |
70 |
0 |
0 |
0 |
|
75-85 |
8 |
80 |
10 |
1 |
8 |
|
85-95 |
3 |
90 |
20 |
2 |
6 |
|
Sum fi = 35 |
Sum fiui = -2 |
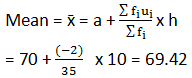
1
The following table shows the ages of the patients admitted in a hospital during a year:
|
Age (in years) |
5-15 |
15-25 |
25-35 |
35-45 |
45-55 |
55-65 |
|
Number of patients |
6 |
11 |
21 |
23 |
14 |
5 |
Find the mode and the mean of the data given above. Compare and interpret the two measures of central tendency.
Answer
Modal class = 35 – 45, l = 35,
class width (h) = 10,
fm = 23,
f1 = 21 and,
f2 = 14
|
Class Interval |
Frequency (fi) |
Mid-point (xi) |
fixi |
|
5-15 |
6 |
10 |
60 |
|
15-25 |
11 |
20 |
220 |
|
25-35 |
21 |
30 |
630 |
|
35-45 |
23 |
40 |
920 |
|
45-55 |
14 |
50 |
700 |
|
55-65 |
5 |
60 |
300 |
|
Sum fi = 80 |
Sum fixi = 2830 |
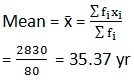
2
The following data gives the information on the observed lifetimes (in hours) of 225
electrical components :
|
Lifetime (in hours) |
0-20 |
20-40 |
40-60 |
60-80 |
80-100 |
100-120 |
|
Frequency |
10 |
35 |
52 |
61 |
38 |
29 |
Determine the modal lifetimes of the components.
Answer
Modal class of the given data is 60–80.
Modal class = 60-80,
l = 60,
fm = 61,
f1 = 52,
f2 = 38 and,
h = 20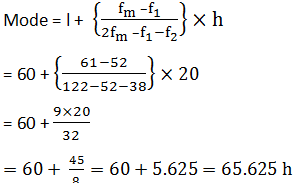
3
The following data gives the distribution of total monthly household expenditure of 200 families of a village. Find the modal monthly expenditure of the families. Also, find the mean monthly expenditure :
|
Expenditure |
Number of families |
|
1000-1500 |
24 |
|
1500-2000 |
40 |
|
2000-2500 |
33 |
|
2500-3000 |
28 |
|
3000-3500 |
30 |
|
3500-4000 |
22 |
|
4000-4500 |
16 |
|
4500-5000 |
7 |
Answer
Modal class = 1500-2000, l = 1500,
fm = 40, f1 = 24, f2 = 33 and h = 500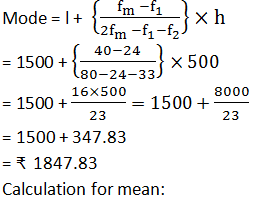
|
Class Interval |
fi |
xi |
di = xi - a |
ui = di/h |
fiui |
|
1000-1500 |
24 |
1250 |
-1500 |
-3 |
-72 |
|
1500-2000 |
40 |
1750 |
-1000 |
-2 |
-80 |
|
2000-2500 |
33 |
2250 |
-500 |
-1 |
-33 |
|
2500-3000 |
28 |
2750 |
0 |
0 |
0 |
|
3000-3500 |
30 |
3250 |
500 |
1 |
30 |
|
3500-4000 |
22 |
3750 |
1000 |
2 |
44 |
|
4000-4500 |
16 |
4250 |
1500 |
3 |
48 |
|
4500-5000 |
7 |
4750 |
2000 |
4 |
28 |
|
fi = 200 |
fiui = -35 |
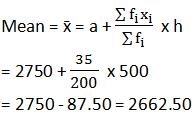
4
The following distribution gives the state wise teacher − student ratio in higher secondary school of India. Find the mode and mean of this data. Interpret , the two measures.
|
Number of students per teacher |
|
|
15-20 20-25 25-30 30-35 35-40 40-45 45-50 50-55 |
3 8 9 10 3 0 0 2 |
Answer
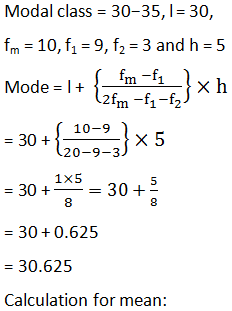
|
Number of Students per teacher |
fi |
Xi |
di= Xi−a |
ui = di/h |
fiui |
|
15-20 |
3 |
17.50 |
−15 |
−3 |
−9 |
|
20-25 |
8 |
22.50 |
−10 |
−2 |
−16 |
|
25-30 |
9 |
27.50 |
−5 |
−1 |
−9 |
|
30-35 |
10 |
32.50 |
0 |
0 |
0 |
|
35-40 |
3 |
37.50 |
5 |
1 |
3 |
|
40-45 |
0 |
42.50 |
10 |
2 |
0 |
|
45-50 |
0 |
47.50 |
15 |
3 |
0 |
|
50-55 |
2 |
52.50 |
20 |
4 |
8 |
|
fi= 35 |
fiui=−23 |
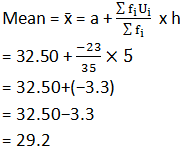
5
The given distribution shows the number of runs scored by some top
batsmen of the world in one day international cricket matches.
|
Runs scored |
Number of batsmen |
|
3000-4000 4000-5000 5000-6000 6000-7000 7000-8000 8000-9000 9000-10000 10000-11000 |
4 18 9 7 6 3 1 1 |
Find the mode of the data.
Answer
Modal class of the given data is 4000–5000.Modal class = 4000-5000 ,
l = 4000, fm = 18, f1 = 4,
f2 = 9 and h = 1000
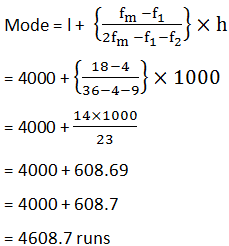
6
A student noted the number of cars passing through a spot on a road for 100 period each of 3 min and summarized it in the given below.
|
Number of cars |
0-10 |
10-20 |
20-30 |
30-40 |
40-50 |
50-60 |
60-70 |
70-80 |
|
Frequency |
7 |
14 |
13 |
12 |
20 |
11 |
15 |
8 |
Find the mode of the data.
Answer
Modal class of the given data is 40–50.Modal class = 40-50 ,
l = 40, fm = 20, f1 = 12,
f2 = 11 and h = 10
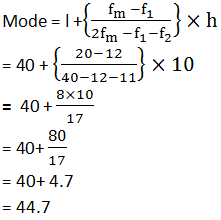
1
The following frequency distribution gives the monthly consumption of electricity of 68 consumers of a locality. Find the median, mean and mode of the data and compare them.
|
Monthly consumption ( in units) |
Number of consumers |
|
65-85 85-105 105-125 125-145 145-165 165-185 185-205 |
4 5 13 20 14 8 4 |
Answer
|
Monthly consumption(in units) |
fi |
cf |
|
65-85 85-105 105-125 125-145 145-165 165-185 185-205 |
4 5 13 20 14 8 4 |
4 9 22 42 56 64 68 |
|
|
N=68 |
|
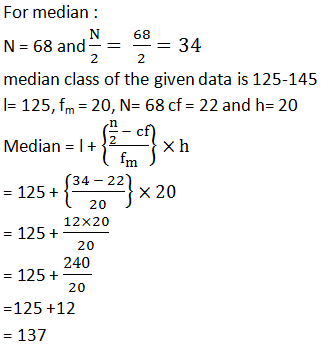
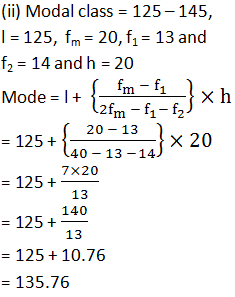
(iii) Calculation for mean:
|
Monthly consumption ( in units) |
fi |
xi |
di = xi−a |
ui =di /h |
fiui |
|
65-85 |
4 |
75 |
−60 |
−3 |
−12 |
|
85-105 |
5 |
95 |
−40 |
−2 |
−10 |
|
105-125 |
13 |
115 |
−20 |
−1 |
−13 |
|
125-145 |
20 |
135 |
0 |
0 |
0 |
|
145-165 |
14 |
155 |
20 |
1 |
14 |
|
165-185 |
8 |
175 |
40 |
2 |
16 |
|
185-205 |
4 |
195 |
60 |
3 |
12 |
|
fi =68 |
fiui = 7 |
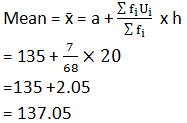
2
If the median of the distribution given below is 28.5, find the value of x and y.
|
Class interval |
Frequency |
|
0-10 10-20 20-30 30-40 40-50 50-60 |
5 X 20 15 y 5 |
|
|
N= 60 |
Answer
|
Class interval |
fi |
cf |
|
0-10 10-20 20-30 30-40 40-50 50-60 |
5 X 20 15 y 5 |
5 5+x 25+x 40+x 40+x+y 45+x+y |
|
|
N=60 |
|
For median :
Given median = 28.5
median class of the given data is 20−30.
l = 20, fm = 20, N= 60, cf = 5+x and h= 10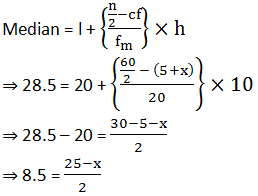
⇒ 17 = 25 – x
⇒ x = 8
From the given table, we have
x+y+45 = 60
⇒ 8+y+45 = 60
⇒ y = 60 – 53
⇒ y = 7
Hence, the value of x = 8 and y = 7.
3
A life insurance agent found the following data for distribution of ages of 100 policy holders. Calculate the median age, if policies are only given to persons having age 18 years onwards but less than 60 years.
|
Age (in years) |
Number of policy holders |
|
Below 20 Below 25 Below 30 Below 35 Below 40 Below 45 Below 50 Below 55 Below 60 |
2 6 24 45 78 89 92 98 100 |
Answer
|
Age (in years) |
fi |
cf |
|
Below 20 20−25 25−30 30−35 35−40 40−45 45−50 50−55 55−60 |
2 = 2 (6−2)=4 (24−6)=18 (45−24)=21 (78−45)=33 (89−78)=11 (92−89)=3 (98−92)=6 (100−98)=2 |
2 6 24 45 78 89 92 98 100 |
|
|
N=100 |
|
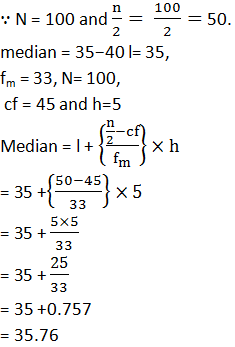
4
The length of 40 leaves of a plant are measured correct to the nearest millimeter and the data obtained is represented in the following table :
Find the median length of the leaves.
|
Length (in mm) |
Number of leaves |
|
118-126 127-135 136-144 145-153 154-162 163-171 172-180 |
3 5 9 12 5 4 2 |
Answer
Since, given classes is not continuous, so it needs to be converted into continuous classes for finding the
median, The classes, then change to 117.5-126.5, 126.5-135.5,...171.5-180.5.
|
Length (in mm) |
fi |
cf |
|
117.5−126.5 126.5−135.5 135.5−144.5 144.5−153.5 153.5−162.5 162.5−171.5 171.5−180.5 |
3 5 9 12 5 4 2 |
3 8 17 29 34 38 40 |
|
|
N=40 |
|
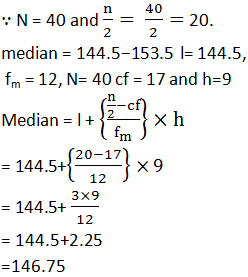
5
The following table gives the distribution of the life time of 400 neon lamps.
Find the median life time of a lamp.
|
Life time (in hours) |
Number of lamps |
|
1500-2000 2000-2500 2500-3000 3000-3500 3500-4000 4000-4500 4500-5000 |
14 56 60 86 74 62 48 |
Answer
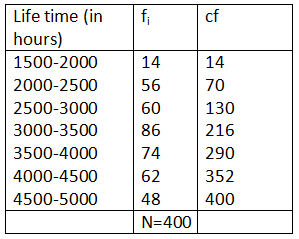
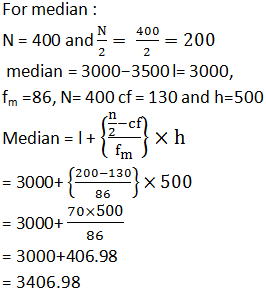
6
100 surnames were randomly picked up from a local telephone directory and the frequency distribution of the number of letters in the English alphabets in the surnames was obtained as follows :
|
Number of letters |
1-4 |
4-7 |
7-10 |
10-13 |
13-16 |
16-19 |
|
Number of surnames |
6 |
30 |
40 |
16 |
4 |
4 |
Determine the median number of letter in the surnames. Find the mean number of letters in the surnames? Also, find the modal size of the surnames.
Answer

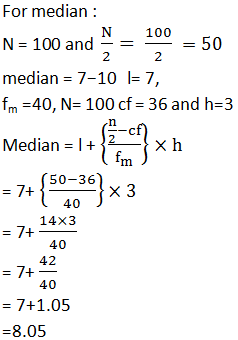
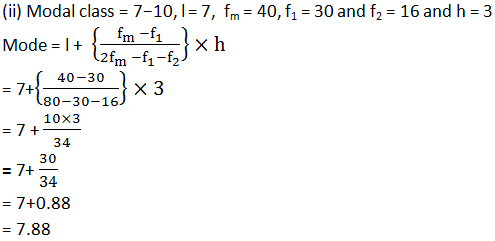
(iii) Calculation for mean:
|
Number of letters |
fi |
xi |
di = xi−a |
ui = di /h |
fiui |
|
1−4 4−7 7−10 10−13 13−16 16−19 |
6 30 40 16 4 4 |
2.5 5.5 8.5 11.5 14.5 17.5 |
−6 −3 0 3 6 9 |
−2 −1 0 1 2 3 |
−12 −30 0 16 8 12 |
|
fi=100 |
fiui=6 |
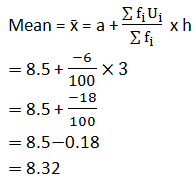
7
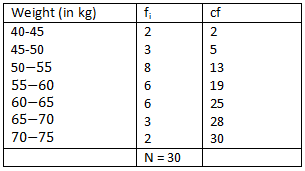
The distribution below gives the weights of 30 students of a class. Find the median weight of the students.
|
Weight (in kg) |
40-45 |
45-50 |
50-55 |
55-60 |
60-65 |
65-70 |
70-75 |
|
Number of students |
2 |
3 |
8 |
6 |
6 |
3 |
2 |
Answer
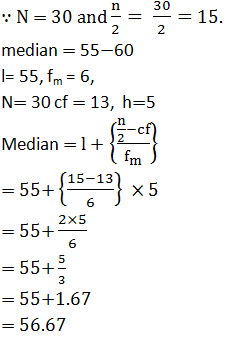
1
The following distribution gives the daily income of 50 workers of a factory.
|
Daily income (in ₹) |
100−120 |
120−140 |
140−160 |
160−180 |
180−200 |
|
Number of workers |
12 |
14 |
8 |
6 |
10 |
Convert the distribution above to a less than type cumulative frequency distribution and draw its ogive.
Answer
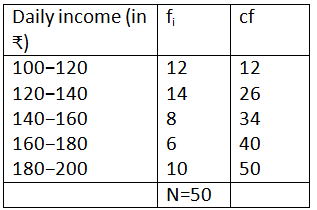
On the graph, we will plot the points (120, 12), (140, 26), (160, 34), (180, 40) and (200,50).
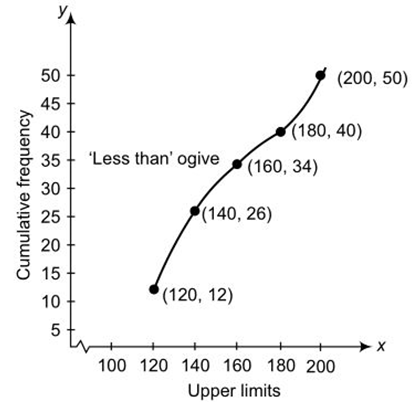
2
Draw a less than ogive for the given data. Hence, obtain the median weight from the graph and verify the result by using the formula.
Answer
![]()
To draw the ‘less than’ type ogive, we plot the points (38, 0), (40, 3), (42, 5), (44, 9), (46, 14), (48, 28), (50, 32) and (52, 35) on the graph. Point 17.5 taking on y-axis draw a line parallel to x-axis meet at a point P′ and draw a perpendicular line from P′ to the x-axis, the intersection point of X-axis is the median.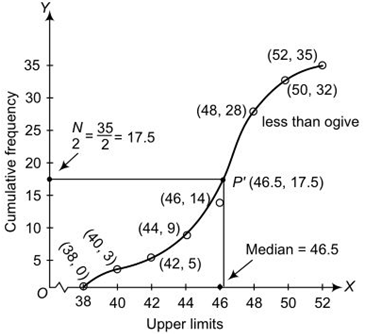
Median from the graph = 46.5 kg
median class of the given data is 46−48.
l = 46, fm = 14, N= 35, cf = 14 and h= 2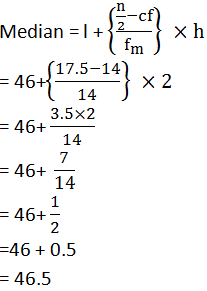
3
The following table gives production yield per hectare of wheat of 100 farms of a village.
|
Production yield |
50-55 |
55-60 |
60-65 |
65-70 |
70-75 |
75-80 |
|
Number of farms |
2 |
8 |
12 |
24 |
38 |
16 |
Change the distribution to a more than type distribution and draw its ogive.
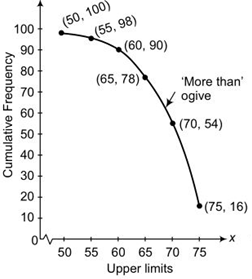
Answer
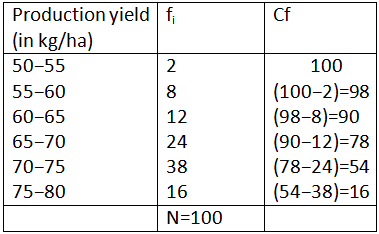
Now, we will draw the ogive by plotting the points (50, 100), (55, 98), (60, 90),
(65, 78), (70, 54) and (75,16).