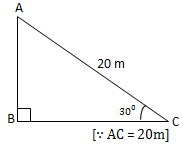
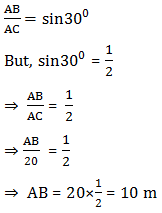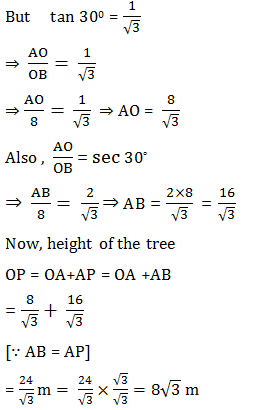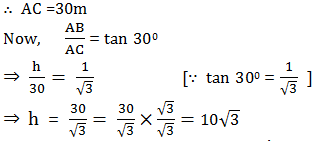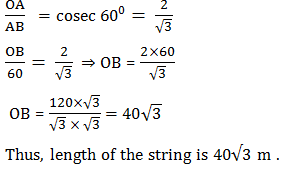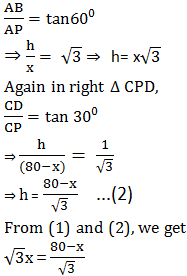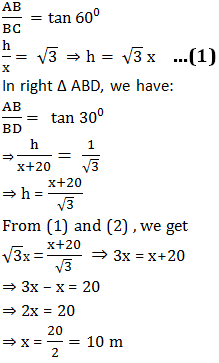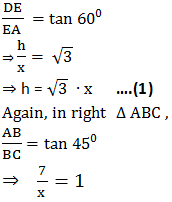A circus artist is climbing a 20 m long rope, which is tightly stretched and tied from the top of a vertical pole to the ground. Find the height of the pole, if the angle made by the rope with the ground level is 30° (see figure).
Answer
In the figure, let AC is the rope and AB is the pole. In right Δ ABC, we have:
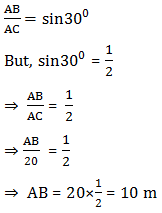
Thus, the required height of the pole is 10 m.
Exercise 9.1
Page Number 203
A tree breaks due to storm and the broken part bends so that the top of the tree touches the ground making an angle 30° with it. The distance between the foot of the tree to the point where the top touches the ground is 8 m. Find the height of the tree.
Answer
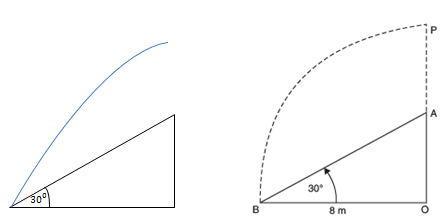
Let the original height of the tree = OP.
It is broken at A and its top is touching the ground at B.
Now, in right Δ AOB, we have
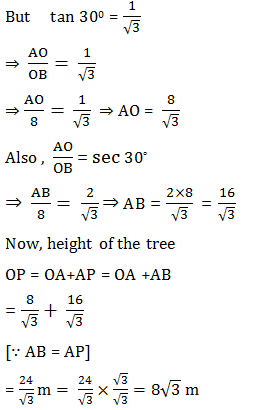
Exercise 9.1
Page Number 203
A contractor plans to install two slides for the children to play in a park. For the children below the age of 5 years, she prefers to have a slide whose top is at a height of 1.5 m, and is inclined at an angle of 30° to the ground, whereas for older children, she wants to have a steep slide at a height of 3 m, and inclined at an angle of 60° to the ground. What should be the length of the slide in each case?
Answer
In the figure, DE is the slide for younger children whereas AC is the slide for older children

In right Δ ABC,
AB = 3m
AC = length of the slide

Exercise 9.1
Page Number 203
The angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of the tower, is 30°. Find the height of the tower.
Answer
In right Δ ABC, AB = the height of the tower. The point C is 30 m away from the foot of the tower,
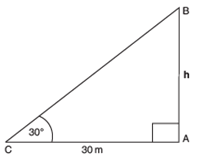
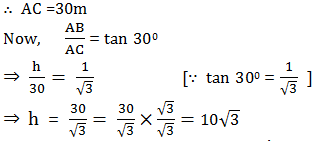
Thus, the required height of the tower is 10√3 m.
Exercise 9.1
Page Number 204
A kite is flying at a height of 60 m above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is 60°. Find the length of the string, assuming that there is no slack in the string.
Answer
Let in the right Δ AOB
,
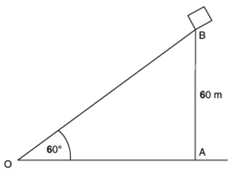
OB = Length of the string
AB = 60 m = Height of the kite,
Exercise 9.1
Page Number 204
A 1.5 m tall boy is standing at some distance from a 30 m tall building. The angle of elevation from his eyes to the top of the building increases from 30° to 60° as he walks towards the building. Find the distance he walked towards the building.
Answer

Here, OA is the building.
In right Δ ABD,

Exercise 9.1
Page Number 204
From a point on the ground, the angles of elevation of the bottom and the top of a transmission tower fixed at the top of a 20 m high building are 45° and 60° respectively. Find the height of the tower.
Answer
Let the height of the building be BC

And height of the tower be CD.
Let the point A be at a distance y metres from the top B of the building.
Now, in right ΔABC,∴ BC = 20 m

Exercise 9.1
Page Number 204
A statue, 1.6 m tall, stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the statue is 60° and from the same point the angle of elevation of the top of the pedestal is 45°. Find the height of the pedestal.
Answer

Exercise 9.1
Page Number 204
The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 50 m high, find the height of the building.
Answer
In the figure, let height of the building = AB = hm
Let CD be the tower.

Exercise 9.1
Page Number 204
Two poles of equal heights are standing opposite each other on either side of the road, which is 80 m wide. From a point between them on the road, the angles of elevation of the top of the poles are 60° and 30° respectively. Find the height of the poles and the distances of the point from the poles.
Answer
Let AB and CD are the two poles such that:
AB = h metres CD = h metres
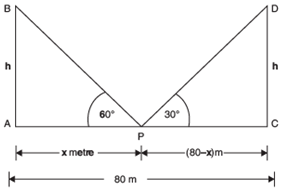
Let ‘P’ be the point on the road such that
AP = x m
CP = (80 − x) m
Now, in right ∆ APB, we have
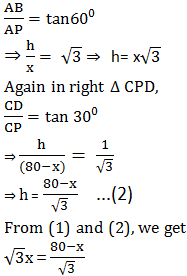
⇒ √3×√3× x = 80−x
⇒ 3x =80−x
⇒ 3x+x =80
⇒ 4x=80
⇒ x = 80/4 =20
⇒ 80−x = 80−20 = 60
Now, from (1) , we have:
h = √3×20 = 1.732×20
= 34.64
Thus,
(i) The required point is 20 m away from the first pole and 60 m away from the second pole.
(ii) Height of each pole = 34.64 m.
Exercise 9.1
Page Number 204
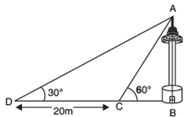
A TV tower stands vertically on a bank of a canal. From a point on the other bank directly opposite the tower, the angle of elevation of the top of the tower is 60°. From another point 20 m away from this point on the line joining this point to the foot of the tower, the angle of elevation of the top of the tower is 30° (see figure). Find the height of the tower and the width of the canal.
Answer
Let the TV Tower be AB = h m.
Let the point ‘C’ be such that
BC = x and CD = 20 m.
Now, in right Δ ABC, we have:
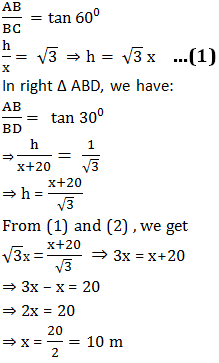
Now, from (1) , we get
h = √3 ×10 = 1.732 ×10 = 17.32
Thus, the height of the tower = 17.32 m.
Also width of the river = 10 m.
Exercise 9.1
Page Number 204
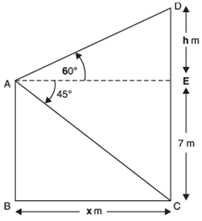
From the top of a 7 m high building, the angle of elevation of the top of a cable tower is 60° and the angle of depression of its foot is 45°. Determine the height of the tower.
Answer
In the figure, let AB be the height of the tower.
∴ AB = 7 metres.
Let CD be the cable tower.
∴ In right Δ DAE, we have
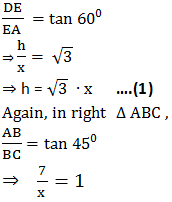
⇒ x = 7
From (1) and (2) ,
h = 7= DE
∴ CD = CE +ED
= 7+ 7√3 = 7(1+√3)m
= 7(1+1.732) m = 7×2.732 m =19.124
Thus, the height of the cable tower is 19.124 m.
Exercise 9.1
Page Number 204
As observed from the top of a 75 m high lighthouse from the sea-level, the angles of depression of two ships are 30° and 45°. If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships.
Answer
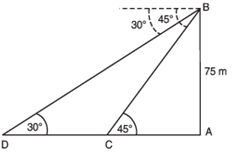
In the figure, let AB represent the light house.
∴ AB = 75 m.
Let the two ships be C and D such that angles of depression from B are 45° and 30° respectively.
Now in right Δ ABC, we have:

Exercise 9.1
Page Number 204
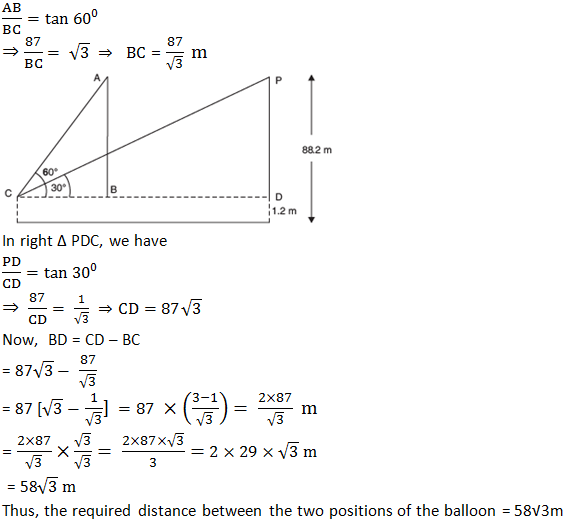
A 1.2 m tall girl spots a balloon moving with the wind in a horizontal line at a height of 88.2 m from the ground. The angle of elevation of the balloon from the eyes of the girl at any instant is 60°. After some time, the angle of elevation reduces to 30° (see figure). Find the distance travelled by the balloon during the interval.
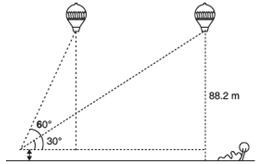
Answer
In the figure, let C be the position of the observer (the girl).
A and P are two positions of the balloon.
CD is the horizontal line from the eyes of the (observer) girl.
Here PD = AB = 88.2 m − 1.2 m = 87 m
In right Δ ABC, we have
Exercise 9.1
Page Number 205
A straight highway leads to the foot of a tower. A man standing at the top of the tower observes a car at an angle of depression of 30°, which is approaching the foot of the tower with a uniform speed. Six seconds later, the angle of depression of the car is found to be 60°. Find the time taken by the car to reach the foot of the tower from this point.
Answer
In the figure, let AB is the height of the tower and C and D be the two positions of the car.

Exercise 9.1
Page Number 205
The angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is 6 m.
Answer
Let the tower be represented by AB in the figure.
Let AB = h metres.
∴ In right ΔABC, we have:

Exercise 9.1
Page Number 205