NCERT Solutions for Chapter 5 समांतर श्रेढ़ीयाँ Class 10 Maths
Book Solutions1
निम्नलिखित स्थितियों में से किन स्थितियों में संबद्ध संख्याओं की सूची समांतर श्रेणी है और क्यों?
(i) प्रत्येक किमी के बाद का टैक्सी का किराया, जबकि प्रथम किमी के लिए किराया 15 रुपए है और प्रत्येक अतिरिक्त किमी के लिए किराया 8 रुपए है।
(ii) किसी बेलन (cylinder) में उपस्थित हवा की मात्रा, जबकि वायु निकालने वाला पंप प्रत्येक बार बेलन की शेष हवा का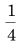 
भाग बाहर निकाल देता है।
भाग बाहर निकाल देता है।(iii) प्रत्येक मीटर की खुदाई के बाद, एक कुआँ खोदने में आई लागत, जबकि प्रथम मीटर खुदाई की लागत के 150 रुपए है और बाद में प्रत्येक मीटर खुदाई की लागत ३ 50 रुपए बढ़ती जाती है।
(iv) खाते में प्रत्येक वर्ष का मिश्रधन, जबकि 10000 रुपए की राशि 8% वार्षिक की दर से चक्रवृद्धि ब्याज पर जमा की जाती है।
Answer
Exercise 5.1
2
दी हुई समांतर श्रेणी के प्रथम चार पद लिखिए, जबकि प्रथम पद a और सार्वअंतर d निम्नलिखित हैं।
Answer
Exercise 5.1
3
निम्नलिखित में से प्रत्येक समांतर श्रेणी के लिए प्रथम पद और सार्वअंतर लिखिए।
Answer
Exercise 5.1
4
निम्नलिखित में से कौन-कौन समांतर श्रेणी हैं? यदि कोई समांतर श्रेणी है, तो इसका सार्वअंतर ज्ञात कीजिए तथा इनके तीन और पद लिखिए।
Answer
Exercise 5.1
1
निम्नलिखित सारणी में, रिक्त स्थानों को भरिए, जहाँ समांतर श्रेणी का प्रथम पद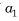
, सार्वअंतर d और nवाँ पद 
है।
, सार्वअंतर d और nवाँ पद है।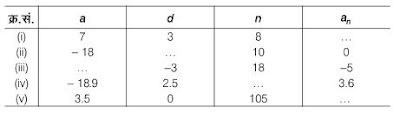Answer
Exercise 5.2
2
निम्नलिखित में सही उत्तर चुनिए और उसका औचित्य दीजिए।
(i) समांतर श्रेणी 10, 7, 4,..., का 30वाँ पद है।
(a) 97 (b) 77 (c) - 77 (d) - 87
(ii) समांतर श्रेणी - 3, -0.5, 2,... का 11वाँ पद है।
(a) 28 (b) 22 (c) -38 (d)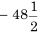 
Answer
Exercise 5.2
3
निम्नलिखित समांतर श्रेणियों में, रिक्त खानों (boxes) के पदों को ज्ञात कीजिए।
Answer
Exercise 5.2
4
समांतर श्रेणी 3, 8, 13, 18, ... का कौन-सा पद 78 हैं?
Answer
Exercise 5.2
5
निम्नलिखित समांतर श्रेणियों में से प्रत्येक श्रेणी में कितने पद हैं?
Answer
Exercise 5.2
6
क्या समांतर श्रेणी 11, 8, 5, 2, ... का एक पद -150 है? क्यों?
Answer
Exercise 5.2
7
उस समांतर श्रेणी का 31वाँ पद ज्ञात कीजिए जिसका 11वाँ पद 38 है और 16वाँ पद 73 है।
Answer
Exercise 5.2
8
एक समांतर श्रेणी में 50 पद हैं, जिसका तीसरा पद 12 है और अंतिम पद 106 है। इसका 29वाँ पद ज्ञात कीजिए।
Answer
Exercise 5.2
9
यदि किसी समांतर श्रेणी के तीसरे और नौवें पद क्रमशः 4 और - 8 हैं, तो इसका कौन-सा पद शून्य होगा?
Answer
Exercise 5.2
10
किसी समांतर श्रेणी का 17वाँ पद उसके 10वें पद से 7 अधिक है। इसका सार्वअंतर ज्ञात कीजिए।
Answer
Exercise 5.2
11
समांतर श्रेणी 3, 15, 27, 39, ... का कौन-सा पद 54वें पद से 132 अधिक होगा?
Answer
Exercise 5.2
12
दो समांतर श्रेणी का सार्वअंतर समान है। यदि इनके 100वें पदों का अंतर 100 है, तो । इनके 1000 वें पदों का अंतर क्या होगा?
Answer
Exercise 5.2
13
तीन अंकों वाली कितनी संख्याएँ 7 से विभाज्य हैं?
Answer
Exercise 5.2
14
10 और 250 के बीच में 4 के कितने गुणज हैं?
Answer
हल : हम देखते हैं कि 12, 10 और 250 के बीच प्रथम पूर्णांक हैं, जो 4 का गुणज है। जब हम 250 को 4 से भाग करते हैं, तो 2 शेष बचता है। 250 - 2 = 248
4 से विभाज्य सबसे बड़ी संख्या होगी, जोकि 10 और 250 के अंतर्गत आती है।
तब, प्रथम पद (a) = 12, अंतिम पद (/) =248, सार्वअंतर (d) = 4
माना श्रेणी के पदों की संख्या n है।
10 और 250 के बीच में 4 के 60 गुणज हैं।
Exercise 5.2
15
n के किस मान के लिए, दोनों समांतर श्रेणियों 63, 65, 67, ... और 3, 10, 17, ... के n वें पद बराबर होंगे?
Answer
हल : यदि समांतर श्रेणियों 63, 65, 67, ... और 3, 10, 17, ... के nवें पद समान हैं। तब,
प्रथम श्रेणी का प्रथम पद = 63
सार्वअंतर = 65-63 =2
और द्वितीय श्रेणी का प्रथम पद = 3
सार्वअंतर = 10-3=7
प्रश्नानुसार,
दोनों समांतर श्रेणी का n वाँ पद समान हैं।
63 + (n-2)2 = 3 + (n-1)7
⇒ 2(n-1) - (n-1)7 = 3 - 63 ⇒ 2n - 2 - 7n + 7 = - 60
⇒ - 5n + 5 = -60 ⇒ -5n = -60 - 5
⇒ -5n = - 65
n =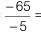 
13
13अतः दी गई दोनों श्रेणियों का 13वें पद सामान हैं।
Exercise 5.2
16
वह समांतर श्रेणी ज्ञात कीजिए जिसका तीसरा पद 16 है और 7वाँ पद 5वें पद से 12 अधिक है।
Answer
हल : माना समांतर श्रेणी का प्रथम पद a और सार्वअंतर d है।
Exercise 5.2
17
समांतर श्रेणी 3, 8, 13, ..., 253 में अंतिम पद से 20 वाँ पद ज्ञात कीजिए।
Answer
हल: दिया है,
अंतिम पद (l) = 253
सार्वअंतर (d) = 8-3=5
अंत से 20वॉ पद = l- (n-1)d = 253- (20-1) x5
= 253-19x5=253-95 = 158
Exercise 5.2
18
किसी समांतर श्रेणी के चौथे और 8वें पदों का योग 24 है तथा छठे और 10वें पदों का योग 44 है। इस समांतर श्रेणी के प्रथम तीन पद ज्ञात कीजिए।
Answer
हल: माना प्रथम पद a और सार्वअंतर d है।
प्रश्नानुसार,
समी (ii) में से समी (i) को घटाने पर,
2d = 10, d = 5
d का मान समी (i) में रखने पर,
a + 25 = 12, a = 12-25 =-13
अतः समांतर श्रेणी के प्रथम तीन पद,
a = -13
a+d = -13+ 5 = -8 और
a+2d = -13+ 10=-3 अर्थात् श्रेणी के तीन पद क्रमशः -13, - 8 और -3 हैं
Exercise 5.2
19
सुब्बाराव ने 1995 में 5000 रुपए के मासिक वेतन पर कार्य आरंभ किया और प्रत्येक वर्ष 200 रुपए की वेतन वृद्धि प्राप्त की। किस वर्ष में उसका वेतन 7000 रुपए हो जाएगा ?
Answer
हल : वर्षों 1995, 1996, 1997, ... आदि में सुब्बाराव द्वारा प्राप्त किया गया वेतन ₹5000, ₹5200, ₹5400, ..., ₹7000 हैं।
अतः 5000, 5200, 5400, ..., 7000 समांतर श्रेणी में है।
माना श्रेणी में पदों की संख्या n है।
⇒ 7000 = a + (n-1)d [:: a = a + (n-1)d]
⇒ 7000 = 5000 + (n-1)1200 ⇒ 7000 - 5000 = (n-1)200
⇒ 
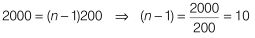
⇒ n = 10 + 1 = 11
अतः नौकरी के 11वें वर्ष में अर्थात् 2005 में सुब्बाराव का वार्षिक वेतन ₹7000 हो जाएगा।
Exercise 5.2
20
रामकली ने किसी वर्ष के प्रथम सप्ताह में ₹5 की बचत की और फिर अपनी साप्ताहिक बचत ₹1,75 बढ़ाती गई। यदि nवें सप्ताह में उसकी साप्ताहिक बचत ₹20.75 हो जाती है, तो n ज्ञात कीजिए।
Answer
हल : रामकली की साप्ताहिक बचत क्रमशः₹5 +(₹5 + ₹1.75)+(₹5 + 2x₹1.75) + (₹5+ 3x ₹1.75) ....
अर्थात् ₹5, ₹6.75, ₹8.50, ₹10.25, .....
माना रामकली n सप्ताह में ₹20.75 बचाएगी।
प्रश्नानुसार
अतः रामकली 10 सप्ताह में ₹20.75 बचाएगी।
Exercise 5.2
1
निम्नलिखित समांतर श्रेणियों का योग ज्ञात कीजिए।
(i) 2, 7, 12, ..., 10 पदों तक
(ii) - 37, - 33, - 29, ..., 12 पदों तक
(iii) 0.6, 1.7, 2.8, ..., 100 पदों तक
Answer
हल: (i) माना दी गई समांतर श्रेणी का प्रथम पद a और सार्वअंतर d है।
दिया है, a =2,d=7-2 = 5, n = 10
∴ समांतर श्रेणी के n पदों का योगफल,
Exercise 5.3
2
नीचे दिए हुए योगफलों को ज्ञात कीजिए।
Answer
Exercise 5.3
3
एक समान्तर श्रेणी में,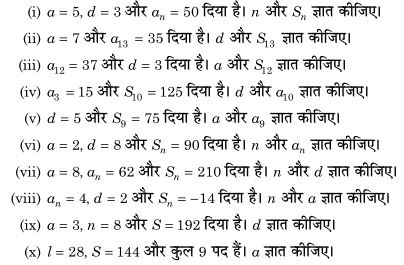
Answer
Exercise 5.3
4
686 योग प्राप्त करने के लिए, समांतर श्रेणी 9, 17, 25, ...के कितने पद लेने चाहिए?
Answer
Exercise 5.3
5
किसी समांतर श्रेणी का प्रथम पद 5 से अंतिम पद 45 और योग 400 है। पदों की संख्या और सार्वअंतर ज्ञात कीजिए।
Answer
Exercise 5.3
6
किसी समांतर श्रेणी के प्रथम और अंतिम पद क्रमशः 17 और 350 है। यदि सार्वअंतर 9 है, तो इसमें कितने पद हैं और इनका योग क्या है?
Answer
Exercise 5.3
7
उस समांतर श्रेणी के प्रथम 22 पदों का योग ज्ञात कीजिए, जिसमें d = 7 है और 22वाँ पद 149 है।
Answer
Exercise 5.3
8
उस समांतर श्रेणी के 51 पदों का योग ज्ञात कीजिए, जिसके दूसरे और तीसरे पद क्रमशः 14 और 18 हैं।
Answer
Exercise 5.3
9
यदि किसी समांतर श्रेणी के प्रथम 7 पदों का योग 49 है और प्रथम 17 पदों का योग 289 है, तो इसके प्रथम n पदों का योग ज्ञात कीजिए।
Answer
Exercise 5.3
10
दर्शाइए कि 
से एक समांतर श्रेणी बनती है, यदि 
नीचे दिए अनुसार परिभाषित है।
से एक समांतर श्रेणी बनती है, यदि नीचे दिए अनुसार परिभाषित है। (i) 
(ii) 
साथ ही, प्रत्येक स्थिति में, प्रथम 15 पदों का योग ज्ञात कीजिए।
Answer
Exercise 5.3
11
यदि किसी समांतर श्रेणी के प्रथम n पदों का योग 
है, तो इसका प्रथम पद (अर्थात् 
) क्या है? प्रथम दो पदों का योग क्या हैं? दूसरा पद क्या है? इसी प्रकार, तीसरे, 10वें और nवें पद ज्ञात कीजिए।
है, तो इसका प्रथम पद (अर्थात् 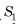) क्या है? प्रथम दो पदों का योग क्या हैं? दूसरा पद क्या है? इसी प्रकार, तीसरे, 10वें और nवें पद ज्ञात कीजिए। Answer
Exercise 5.3
12
ऐसे प्रथम 40 धन पूर्णांकों का योग ज्ञात कीजिए जो 6 से विभाज्य है।
Answer
हल: 6 से विभाज्य 40 धन पूर्णांक 6, 12, 18, ...
प्रथम पद = 6, सार्वअंतर, d = 12-6 = 6, n= 40
Exercise 5.3
13
8 के प्रथम 15 गुणजों का योग ज्ञात कीजिए।
Answer
हल: 8 के प्रथम 15 गुणज 8✕1, 8✕2, 8✕3, 8✕4, .........8✕15 ⇒ 8, 16, 24, 32, ............120
प्रथम पद(a) = 8, सार्वअंतर, d = 16-8 = 8, n= 15 और l=120
Exercise 5.3
14
0 और 50 के बीच की विषम संख्याओं का योग ज्ञात कीजिए।
Answer
0 और 50 के बीच की विषम संख्याओं का योग ज्ञात कीजिए।
हल 0 और 50 के बीच विषम संख्याएँ क्रमशः 1, 3, 5,..., 49 हैं।
यहाँ, प्रथम पद (a) = 1, अंतिम पद (/) = 49 सार्वअंतर (d) = 3-1=2
माना पदों की संख्या n है
Exercise 5.3
15
निर्माण कार्य से संबंधित किसी ठेके में, एक निश्चित तिथि के बाद कार्य को विलंब से पूरा करने के लिए, जुर्माना लगाने का प्रावधान इस प्रकार है-पहले दिन के लिए ₹200, दूसरे दिन के लिए ₹250, तीसरे दिन के लिए ₹300 इत्यादि अर्थात् प्रत्येक उतरोत्तर दिन का जुर्माना अपने से ठीक पहले दिन के जुर्माने से ₹50 अधिक है। एक ठेकेदार को जुर्माने के रूप में कितनी राशि अदा करनी पड़ेगी, यदि वह इस कार्य में 30 दिन का विलंब कर देता है?
Answer
हल : प्रत्येक लगातार बढ़ते दिन का दंड, पिछले दिन से है 50 अधिक है। अतः पहले, दूसरे, तीसरे, ... आदि दिनों का दंड समांतर श्रेणी में होगा।
माना n दिनों की पेनल्टी (दंड) =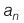 
.:.200, 250, 300, ... समांतर श्रेणी में हैं।
यदि ठेकेदार कार्य को 30 दिन देरी से करता है, तब उसे दंड के रूप में कर देना होगा
Exercise 5.3
16
किसी स्कूल के विद्यार्थियों को उनके समग्र शैक्षिक प्रदर्शन करने के लिए 7 नकद पुरस्कार देने के लिए ₹700 की राशि रखी गई हैं। यदि प्रत्येक पुरस्कार अपने से ठीक पहले पुरस्कार से ₹20 कम है, तो प्रत्येक पुरस्कार का मान ज्ञात कीजिए।
Answer
हल: माना पुरस्कार क्रमशः a + 60, a + 40, a + 20, a, a -20, a - 40 और a-60 हैं।
प्रश्नानुसार, a + 60 + a + 40 + a + 20 + a + a-20 + a - 40 + a - 60 = 700
⇒7a = 700 ⇒ a = 700/7 = 100
अतः सात पुरस्कार क्रमशः 100 + 60, 100 + 40, 100 + 20, 100, 100-20, 100 - 40 और 100-60 है।
अर्थात् 160, 140, 120, 100, 80, 60, 40 हैं।
Exercise 5.3
17
एक स्कूल के विद्यार्थियों ने वायु प्रदूषण कम करने के लिए स्कूल के अंदर और बाहर पेड़ लगाने के बारे में सोचा। यह निर्णय लिया गया कि प्रत्येक कक्षा का प्रत्येक अनुभाग अपनी कक्षा की संख्या के बराबर पेड़ लगाएगा। उदाहरणार्थ, कक्षा I का एक अनुभाग 1 पेड़ लगाएगा, कक्षा II का एक अनुभाग 2 पेड़ लगाएगा, कक्षा III का एक अनुभाग 3 पेड़ लगाएगा, इत्यादि और ऐसा कक्षा XII तक के लिए चलता रहेगा। प्रत्येक कक्षा के तीन अनुभाग हैं। इस स्कूल के विद्यार्थियों द्वारा लगाए गए कुल पेड़ों की संख्या कितनी होगी?
Answer
हल: प्रश्नानुसार, प्रत्येक कक्षा के तीन वर्ग हैं। इसलिए प्रत्येक वर्ग ने पौधे लगाए अर्थात् कक्षा ।, कक्षा ।।, कक्षा III, ..., कक्षा XII द्वारा लगाए गए पौधे हैं।
1x3, 2x3, 3x3, ..., 12x3,
स्पष्ट है कि 3, 6, 9, ....., 36. समांतर श्रेणी में हैं।
यहाँ, प्रथम पद (a) = 3 सार्वअंतर (d) = 6-3 = 3
अंतिम पद (/) = 36
अब, समांतर श्रेणी का nवाँ पद, a = a + (n-1)d = l
Exercise 5.3
18
केंद्र A से प्रारंभ करते हुए बारी-बारी से केंद्रों A और B को लेते हुए, त्रिज्याओं 0.5 सेमी, 1.0 सेमी, 1.5 सेमी, 20 सेमी ... वाले उतरोत्तर अर्द्धवृत्तों को खींचकर एक सर्पिल (spiral) बनाया गया है, जैसा कि आकृति में दर्शाया गया है। तेरह क्रमागत अर्द्धवृत्तों से बने इस सर्पिल की कुल लंबाई क्या है? (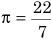 
लीजिए )
लीजिए )[संकेत: क्रमशः A, B, A, B, .....वाले अर्द्धवृत्तों की लम्बाई 
हैं।]
हैं।]Answer
हल:13 क्रमागत अर्द्धवृत्तों को खींचकर एक सर्पिल बनाया गया है जिसकी लंबाई
= (π X 0.5 + π X1.0+ πX1.5 + π X2.0 +... + π X6.5)
= πX 0.5 (1+2+3+...+13)
जोकि समांतर श्रेणी में है।
प्रथम पद (a) = 1, सार्वअंतर (d) =2-1=1
पदों की संख्या, n=13
Exercise 5.3
19
200 लट्ठों (logs) को ढेरी के रूप में इस प्रकार रखा जाता है कि-सबसे नीचे वाली पंक्ति में 20 लट्ठे, उससे अगली पंक्ति में 19 लट्ठे, उससे अगली पंक्ति में 18 लट्ठे, इत्यादि (देखिए आकृति)। ये 200 लट्ठे कितनी पंक्तियों में रखे गए हैं। तथा सबसे ऊपरी पंक्ति में कितने लट्ठे हैं?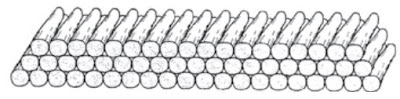
Answer
हल: लट्ठों को प्रत्येक पंक्ति में एक श्रेणी 20, 19, 18, 17,... के रूप में रखा गया है। स्पष्ट है। कि यह समांतर श्रेणी है।
Exercise 5.3
20
एक आलू दौड़ (potato race) में प्रारंभिक स्थान पर एक बाल्टी रखी हुई है जो पहले आलू से 5 मी की दूरी पर है तथा अन्य आलुओं को एक सीधी रेखा में परस्पर 3 मी की दूरियों पर रखा गया है। इस रेखा पर 10 आलु रखे गए हैं। प्रत्येक प्रतियोगी बाल्टी से चलना प्रारंभ करती है, 
निकटतम आलू को उठाती है, उसे लेकर वापस आकर दौड़कर बाल्टी में डालती है, दूसरा आलू उठाने के लिए वापस दौड़ती है, उसे उठाकर वापस बाल्टी में डालती है और वह ऐसा तब तक करती रहती है, जब तक सभी आलू बाल्टी में न आ जाएँ। इसमें प्रतियोगी को कुल कितनी दूरी दौड़नी पड़ेगी?
[संकेत-पहले और दूसरे आलुओं को उठाकर बाल्टी में डालने तक दौड़ी गई दूरी =2x5 + 2x (5+ 3) है।]
Answer
हल : प्रश्नानुसार, एक प्रतियोगी पहला आलू, दूसरा आलू, तीसरा आलू, ... उठाता है।
प्रतियोगी द्वारा तय की गई दूरियाँ 2x5, 2x(5 + 3) 2x(5 + 3 + 3), 2x(5 +3+3+ 3), ...
अर्थात् 10, 16, 22, 28, ... जोकि समांतर श्रेणी में हैं।
प्रथम पद (a) = 10, सार्वअंतर d = 16-10 = 6
पदों की संख्या = 10
Exercise 5.3