NCERT Solutions for Chapter 4 Quadratic Equations Class 10 Maths
Book Solutions1(i)
Answer
We have:
(x + 1)2 = 2 (x − 3)
⇒ x2 + 2x + 1 = 2x − 6
⇒ x2 + 2x + 1 − 2x + 6 = 0
⇒ x2 + 7 = 0
Since x2 + 7 is a quadratic polynomial
∴ (x + 1)2 = 2(x − 3) is a quadratic equation.
1(ii)
Answer
We have:
x2 − 2x = (− 2) (3 − x)
⇒ x2 − 2x
= − 6 + 2x
⇒ x2 − 2x
− 2x + 6 = 0
⇒ x2 − 4x
+ 6 = 0
Since x2 − 4x + 6 is a quadratic
polynomial
∴ x2 − 2x
= (−2) (3 − x) is a quadratic equation.
1(iii)
Answer
We have:
(x − 2) (x + 1) = (x − 1) (x + 3)
⇒ x2 − x
− 2 = x2 + 2x − 3
⇒ x2 − x
− 2 − x2 − 2x + 3 = 0
⇒ −3x + 1 = 0
Since −3x + 1 is a linear polynomial
∴ (x − 2) (x + 1) = (x − 1) (x + 3) is not quadratic
equation.
1(iv)
Answer
We have:
(x − 3) (2x + 1) = x (x + 5)
⇒ 2x2 + x
− 6x −3= x2 + 5x
⇒ 2x2 −
5x − 3 − x2 − 5x =0
⇒ x2 +
10x − 3= 0
Since x2 + 10x − 3 is a quadratic
polynomial
1(v)
Answer
We have:
(x − 3) (2x + 1) = x (x + 5)
⇒ 2x2 + x
− 6x −3= x2 + 5x
⇒ 2x2 −
5x − 3 − x2 − 5x =0
⇒ x2 +
10x − 3= 0
Since x2 + 10x − 3 is a quadratic
polynomial
1(vi)
Answer
We have:
x2 + 3x + 1 = (x − 2)2
⇒ x2 + 3x
+ 1 = x2 − 4x + 4
⇒ x2 + 3x
+ 1 − x2 + 4x −4= 0
⇒ 7x − 3 = 0
Since 7x − 3 is a linear polynomial
∴ x2 + 3x + 1 = (x − 2)2 is not
a quadratic equation.
1(vii)
Answer
We have:
⇒ x3 + 3x2(2) + 3x(2)2 + (2)3 = 2x3 − 2x
⇒ x3 + 6x2 + 12x + 8 = 2x3 − 2x
⇒ x3 + 6x2 + 12x + 8 − 2x3 + 2x = 0
⇒− x3 + 6x2 + 14x + 8 = 0
Since −x3 + 6x2 + 14x + 8 is a polynomial of degree 3
∴ (x + 2)3 = 2x(x2 − 1) is not a quadratic equation.
1(viii)
Answer
We have:
⇒ x3 + 3x2(2) + 3x(2)2 + (2)3 = 2x3 − 2x
⇒ x3 + 6x2 + 12x + 8 = 2x3 − 2x
⇒ x3 + 6x2 + 12x + 8 − 2x3 + 2x = 0
⇒− x3 + 6x2 + 14x + 8 = 0
Since −x3 + 6x2 + 14x + 8 is a polynomial of degree 3
∴ (x + 2)3 = 2x(x2 − 1) is not a quadratic equation.
2(i)
Represent the following situations in the form of quadratic equations.
(i) The area of a rectangular plot is 528 m2. The length of the plot (in metres) is one more than twice its breadth. We need to find the length and breadth of the plot.
Answer
Let the breadth =
x metres
∵ Length = 2 (Breadth) +
1
∴ Length = (2x + 1) metres
Since Length × Breadth = Area
∴ (2x + 1) × x = 528
⇒ 2x2 + x
= 528
⇒ 2x2 + x
− 528 = 0
Thus, the required quadratic equation is 2x2 + x− 528 = 0
2(ii)
(ii) The product of two consecutive positive integers is 306. We need to find the integers.
Answer
Let the two consecutive numbers be x and (x + 1).
∵Product of the numbers =
306
∴ x (x + 1) = 306
⇒ x2 + x
= 306
⇒ x2 + x
− 306 = 0
2(iii)
Answer
Let the present age = x
∴ Mother’s age = (x + 26) years
After 3 years
His age = (x + 3) years
Mother’s age = [(x + 26) + 3] years
=(x + 29) years
According to the condition,
[Product of their ages after 3 years] = 360
⇒ (x + 3) × (x + 29) = 360
⇒ x2 + 29x + 3x + 87 = 360
⇒ x2 + 29x + 3x + 87 − 360 = 0
⇒ x2 + 32x − 273 = 0
Thus, the required quadratic equation is
x2 + 32x − 273 = 0
2(iv)
Answer
In first case,
Let the speed of the train = u km/hr
Distance covered = 480 km
Time taken = Distance ÷ Speed

Thus, the required quadratic equation is u2 − 8u – 1280 = 0
1(i)
(i) x2 – 3x – 10 = 0
Answer
We have:
x2 − 3x − 10 = 0
⇒ x2 − 5x + 2x − 10 = 0
⇒ x (x − 5) + 2 (x − 5) = 0
⇒ (x − 5) (x + 2) = 0 Either x − 5=0
⇒ x = 5 or x + 2 = 0
⇒ x = − 2
Thus, the required roots are x = 5 and x = −2.
1(ii)
Answer
We have:
2x2 + x − 6 = 0
⇒ 2x2 +
4x − 3x − 6 =0
⇒ 2x(x + 2) − 3 (x + 2) =
0
⇒ (x + 2) (2x − 3) = 0
Either x + 2 = 0 ⇒ x = −2
or 2x − 3= 0 ⇒ x = 3/2
1(iii)
Answer
We have:
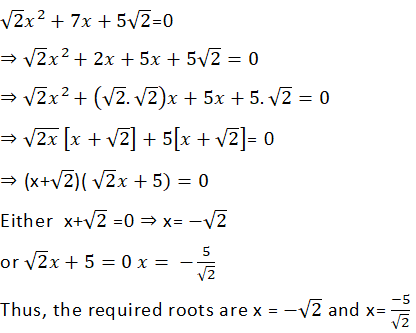
1(iv)
Answer
We have:
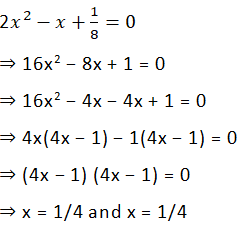
Thus, the required roots are = x = 1/4 and x = 1/4
1(v)
Answer
We have:
100x2 − 20x + 1 = 0
⇒ 100x2 −
10x − 10x + 1 = 0
⇒ 10x (10x − 1) − 1 (10x
− 1) = 0
⇒ (10x − 1) (10x − 1) = 0
⇒ (10x − 1) = 0 and (10x
− 1) = 0
⇒ x = 1/10 and x = 1/10
2
(i) John and Jivanti together have 45 marbles. Both of them lost 5 marbles each, and the product of the number of marbles they now have is 124. Find out how many marbles they had to start with.
(ii) A cottage industry produces a certain number of toys in a day. The cost of production of each toy (in rupees) was found to be 55 minus the number of toys produced in a day. On a particular day, the total cost of production was Rs 750. Find out the number of toys produced on that day.
Answer
After losing 5 marbles,
Number of John's marbles = x - 5
Number of Jivanti's marbles = 45 - x - 5 = 40 - x
It is given that the product of their marbles is 124.
⇒ x2 – 36x - 9x + 324 = 0
⇒ x(x - 36) -9(x - 36) = 0
⇒ (x - 36)(x - 9) = 0 [∵ (-9) × (-36) = 324 and (-9)+(-36)=-4]
Either x - 36 = 0 or x - 9 = 0
⇒ x = 36 or x = 9
If the number of John's marbles = 36,
Then, number of Jivanti's marbles = 45 - 36 = 9
If number of John's marbles = 9,
Then, number of Jivanti's marbles = 45 - 9 = 36
It is given that, total production of the toys = Rs 750
⇒ x = 25 or x = 30
Hence, the number of toys will be either 25 or 30.
3
Answer
Here, sum of the numbers is 27.
Let one of the numbers be x.
∴ Other number = 27 − x
According to the condition,
Product of the numbers = 182
⇒ 27x − x2 = 182
⇒− x2 + 27x − 182 = 0
⇒ x2 − 27x + 182 = 0
⇒ x(x - 13) -14(x - 13) = 0
⇒ (x - 13)(x -14) = 0 [∵ −27 = (−13)+(−14) and (-13)×(-14)= 182]
Either x = -13 = 0 or x - 14 = 0
⇒ x = 13 or x = 14
If first number = 13, then
Other number = 27 - 13 = 14
If first number = 14, then
Other number = 27 - 14 = 13
Therefore, the numbers are 13 and 14.
4
Find two consecutive positive integers, sum of whose squares is 365.
Answer
Let the two consecutive positive integers be x and (x + 1).
Since the sum of the squares of the numbers = 365
∴ x2 + (x + 1)2 = 365
⇒ x2 + [x2 + 2x + 1] = 365
⇒ x2 + x2 + 2x + 1 = 365
⇒ 2x2 + 2x + 1 − 365 = 0
⇒ 2x2 + 2x − 364 = 0
⇒ x2 + x − 182 = 0
⇒ x2 +14x −13x −182 = 0
⇒ x(x+14) − 13(x+14)=0 [∵ +14 −13= 1and 14×(-13) = −182]
⇒ (x+14)(x−13) = 0
Either x + 14 = 0 ⇒ x = − 14
or x − 13 = 0 ⇒ x = 13
Since x has to be a positive integer
∴ x = 13
⇒ x + 1 = 13 + 1 = 14
5
Answer
Let the base of the right triangle be x cm.
Its altitude = (x - 7) cm
From Pythagoras theorem, we have
⇒ x2 + x2 + 49 - 14x = 169
⇒ 2x2 - 14x - 120 = 0
⇒ x2 - 7x - 60 = 0
⇒ x2 - 12x + 5x - 60 = 0
⇒ x(x - 12) + 5(x - 12) = 0
⇒ (x - 12)(x + 5) = 0
Either x - 12 = 0 or x + 5 = 0,
⇒ x = 12 or x = - 5
Since sides are positive, x can only be 12.
Therefore, the base of the given triangle is 12 cm and the altitude of this triangle will be (12 - 7) cm = 5 cm.
6
Answer
Let the number of articles produced in a day = x
∴ Cost of production of
each article = ₹ (2x + 3)
According to the condition,
Total cost = 90
⇒ x × (2x + 3) = 90
⇒ 2x2 +
3x = 90
⇒ 2x2 +
3x − 90 = 0
⇒ 2x2 −
12x + 15x − 90 = 0
⇒ 2x (x − 6) + 15 (x − 6)
= 0
⇒ (x − 6) (2x + 15) = 0
Either x − 6 = 0 ⇒ x = 6
or 2x + 15 = 0 ⇒ x = -15/2
But the number of articles cannot be negative.
x = -15/2 is not required
⇒ x = 6
Thus, the required number of articles produced is 6 and the cost of each article is ₹15.
1(i)
Find the roots of the following quadratic equations, if they exist, by the method of completing the square:
(i) 2x2 – 7x +3 = 0
Answer
2x2−7x + 3 = 0
Dividing throughout by the co-efficient of x2, we get
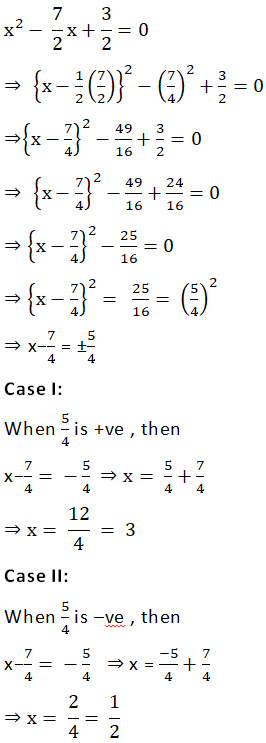
Thus required roots are, x = 3 and x = 1/2
1(ii)
(ii) 2x2 + x – 4 = 0
Answer
We have:
2x2 + x − 4 = 0
Dividing throughout by 2,
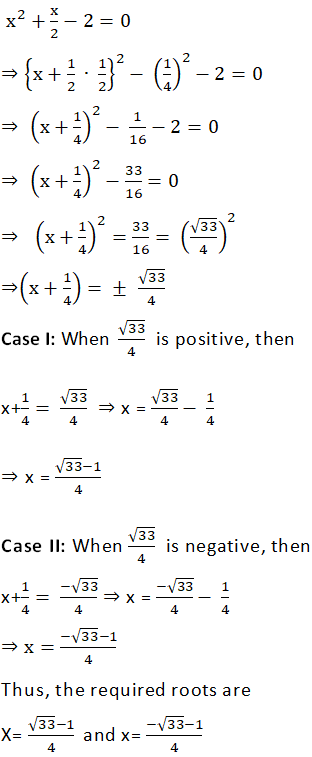
1(iii)
(iii) 4x2 + 4√3x + 3 = 0
Answer
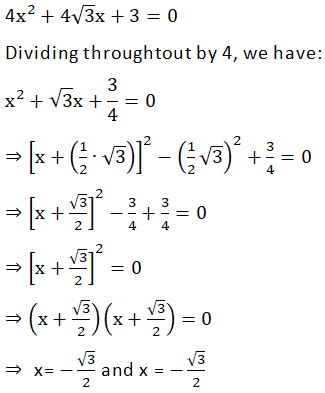
1(iv)
Answer
2x2 + x + 4 = 0
Dividing throughout by 2, we have:
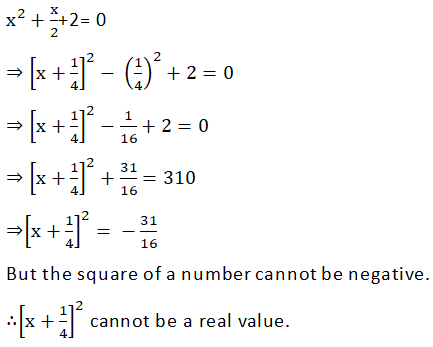
So, no real roots exist.
There is no real value of x satisfying the given equation.
2
Answer
(i) 2x2−7x + 3 = 0
Comparing the given equation with ax2 + bx + c = 0, we have:
a = 2
b = − 7
c = 3
∴ b2 − 4ac =(−7)2 − 4(2)(3)
⇒ 49 − 24 = 25 ≥ 0
Since b2 − 4ac > 0
∴ The given equation has real roots.
The roots are given by,

(ii) 2x2 + x−4 = 0
Comparing the given equation with ax2 + bx + c = 0, we have:
a = 2
b = 1 c = − 4
∴ b2 − 4ac = (1)2 − 4 (2) (− 4)
= 1 + 32
= 33 > 0
Since b2 − 4ac > 0
∴ The given equation has equal roots.
The roots are given by

(iii) 4x2 + 4√3x + 3 = 0
Comparing the given equation with ax2 + bx + c = 0, we have:
a = 4
b = 43
c = 3
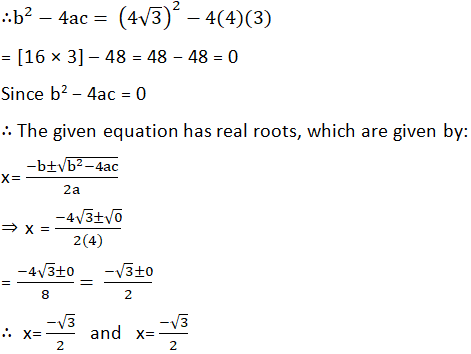
(iv) 2x2 + x + 4 = 0
Comparing the given equation with ax2 + bx + c = 0, we have:
a = 2
b = 1
c = 4
∴ b2 − 4ac = (1)2 − 4(2)(4)
= 1 − 32 = − 31 < 0
Since b2 − 4ac is less than 0, therefore the given equation does not have real roots.
3(i)
(i) x-1/x = 3, x ≠ 0
Answer
x−1/x = 3
⇒ x2 − 1= 3 x
⇒ x2 − 3x − 1 = 0 ...(1)
Comparing (1) with ax2 + bx + c = 0, we have:
a = 1
b = − 3
c = − 1
= 9 + 4 = 13 > 0
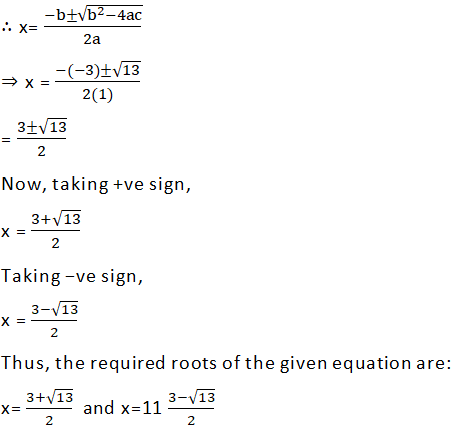
3(ii)
Answer
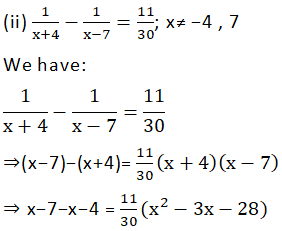
⇒ − 11 × 30 = 11 (x2 − 3x − 28)
⇒ − 30 = x2 −
3x − 28
⇒ x2 − 3x
− 28 + 30 = 0
⇒ x2 − 3x
+ 2 = 0
Comparing with ax2 + bx + c = 0, we have:
a =1
b = − 3
c = 2
∴ b2 − 4ac =(− 3)2 − 4(1)(2)
= 9 − 8 = 1 > 0
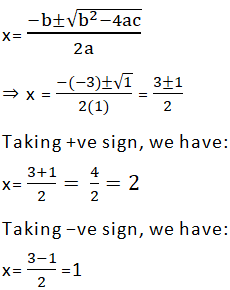
Thus, the roots of the given equation are:
4
Answer
Let the present age of Rehman = x
∴ 3 years ago Rehman’s age = (x − 3) years
5 years later Rehman’s age = (x + 5) years
Now according to the condition,
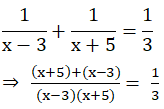
⇒ 3 [x + 5 + x − 3] = (x − 3) (x + 5)
⇒ 3 [2x + 2] = x2 + 2x − 15
⇒ 6x + 6 = x2 + 2x − 15
⇒ x2 + 2x − 6x − 15 − 6=0
⇒ x2 − 4x − 21 = 0 ...(1)
Now, comparing (1) with ax2 + bx + c = 0, we have:
a =1
b = − 4
c = − 21
∴ b2 − 4ac =(− 4)2 − 4 (1)(−21)
= 16 + 84
= 100
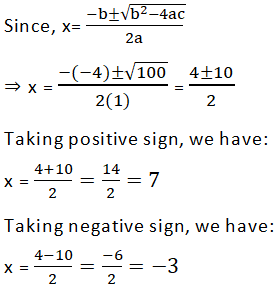
Since age cannot be negative,
∴ x ≠− 3 ⇒ x = 7
So, the present age of Rehman = 7 years.
5
Answer
Let, Shefali’s marks in Mathematics = x
∴ Marks in English = (30 − x) [∵ Sum of their marks in Eng. and Maths = 30]
Now, according to the condition,
(x + 2) × [(30 − x) − 3] = 210
⇒ (x + 2) × (30 − x − 3) = 210
⇒ (x + 2) (−x + 27) = 210
⇒ −x2 + 25x + 54 = 210
⇒ −x2 + 25x + 54 − 210 = 0
⇒ −x2 + 25x − 156 = 0
⇒ x2 − 25x + 156 = 0 ...(1)
Now, comparing (1) with ax2 + bx + c = 0
a = 1
b = −25
c = 156
∴ b2 − 4ac =(−25)2 − 4(1) (156)
= 625 − 624 = 1
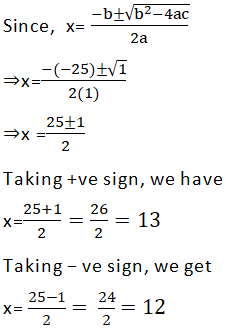
When x = 13, then 30 − 13 = 17
When x = 12, then 30 − 12 = 18
Thus, marks in Maths = 13, marks in English = 17
marks in Maths = 12, marks in English = 18
6
Answer
Let the shorter side (i.e., breadth) = x metres.
∴ The longer side
(length) = (x + 30) metres.
In a rectangle,
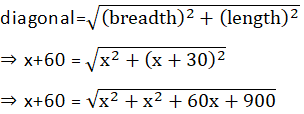
⇒ (x + 60)2 = 2x2 + 60x +
900
⇒ x2 +
120x + 3600 = 2x2 + 60x + 900
⇒ 2x2 − x2 +
60x − 120x + 900 − 3600 = 0
⇒ x2 −
60x − 2700 = 0 ...(1)
Comparing (1) with ax2 + bx + c = 0
∴ a = 1
b = −60
c = −2700
∴ b2 − 4ac =(−
60)2 − 4 (1) (− 2700)
⇒ b2 − 4ac =
3600 + 10800
⇒ b2 − 4ac =
14400
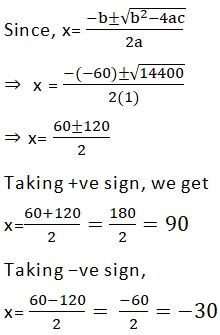
Since breadth cannot be negative,
∴ x ≠−30 ⇒ x = 90
∴ x + 30 = 90 + 30 = 120
Thus, the shorter side = 90 m
The longer side = 120 m.
7
Answer
x2 - y2 = 180 and y2 = 8x
⇒ x2 - 8x = 180
⇒ x2 - 8x - 180 = 0
⇒ x2 - 18x + 10x - 180 = 0
⇒ x(x - 18) +10(x - 18) = 0
⇒ (x - 18)(x + 10) = 0
⇒ x = 18, -10
However, the larger number cannot be negative as 8 times of the larger number will be negative and hence, the square of the smaller number will be negative which is not possible.
Therefore, the larger number will be 18 only.
x = 18
∴ y2 = 8x = 8 × 18 = 144
⇒ y = ±√44 = ±12
∴ Smaller number = ±12
Therefore, the numbers are 18 and 12 or 18 and - 12
8
Answer
Let the speed of the train be x km/hr.Time taken to cover 360 km = 360/x hr.According to the question,
⇒ (x + 5)(360-1/x) = 360
⇒ 360 - x + 1800-5/x = 360
⇒ x2 + 5x + 10x - 1800 = 0
⇒ x(x + 45) -40(x + 45) = 0
⇒ (x + 45)(x - 40) = 0
⇒ x = 40, -45
However, speed cannot be negative.
Therefore, the speed of train is 40 km/h.
9
Answer
Let the time taken by the smaller pipe to fill the tank be x hr.
Time taken by the larger pipe = (x - 10) hr
Part of tank filled by smaller pipe in 1 hour = 1/x
x-10+x/x(x-10) = 8/75
⇒ 2x-10/x(x-10) = 8/75
⇒ 75(2x - 10) = 8x2 - 80x
⇒ 150x - 750 = 8x2 - 80x
⇒ 8x2 - 230x +750 = 0
⇒ 8x2 - 200x - 30x + 750 = 0
⇒ 8x(x - 25) -30(x - 25) = 0
⇒ (x - 25)(8x -30) = 0
⇒ x = 25, 30/8
Time taken by the smaller pipe cannot be 30/8 = 3.75 hours. As in this case, the time taken by the larger pipe will be negative, which is logically not possible.
Therefore, time taken individually by the smaller pipe and the larger pipe will be 25 and 25 - 10 =15 hours respectively.
10
Answer
Let the average speed of passenger train be x km/h.
Average speed of express train = (x + 11) km/h
It is given that the time taken by the express train to cover 132 km is 1 hour less than the passenger train to cover the same distance.
11
Answer
Let the sides of the two squares be x m and y m. Therefore, their perimeter will be 4x and 4yrespectively and their areas will be x2 and y2 respectively.It is given that
4x - 4y = 24
x - y = 6
x = y + 6
Also, x2 + y2 = 468
⇒ (6 + y2) + y2 = 468
⇒ 36 + y2 + 12y + y2 = 468
⇒ 2y2 + 12y + 432 = 0
⇒ y2 + 6y - 216 = 0
⇒ y2 + 18y - 12y - 216 = 0
⇒ y(y +18) -12(y + 18) = 0
⇒ (y + 18)(y - 12) = 0
⇒ y = -18, 12
However, side of a square cannot be negative.
Hence, the sides of the squares are 12 m and (12 + 6) m = 18 m.
1
(i) 2x2 - 3x + 5 = 0
(ii) 3x2 - 4√3x + 4 = 0
(iii) 2x2 - 6x + 3 = 0
Answer
(i) Consider the equation
x2 - 3x + 5 = 0
Comparing it with ax2 + bx + c = 0, we get
a = 2, b = -3 and c = 5
Discriminant = b2 - 4ac
= ( - 3)2 - 4 (2) (5) = 9 - 40
= - 31
As b2 - 4ac < 0,
Therefore, no real root is possible for the given equation.
(ii) 3x2 - 4√3x + 4 = 0
Comparing it with ax2 + bx + c = 0, we get
a = 3, b = -4√3 and c = 4
Discriminant = b2 - 4ac
= (-4√3)2 - 4(3)(4)
= 48 - 48 = 0
As b2 - 4ac = 0,
Therefore, real roots exist for the given equation and they are equal to each other.
And the roots will be -b/2a and -b/2a.-b/2a = -(-4√3)/2×3 = 4√3/6 = 2√3/3 = 2/√3
Therefore, the roots are 2/√3 and 2/√3.
Comparing this equation with ax2 + bx + c = 0, we get
a = 2, b = -6, c = 3
Discriminant = b2 - 4ac
= 36 - 24 = 12
As b2 - 4ac > 0,
2(i)
(i) 2x2 + kx + 3 = 0
Answer
2x2 + kx + 3 = 0
Comparing equation with ax2 + bx + c = 0, we get
a = 2, b = k and c = 3
Discriminant = b2 - 4ac
= k2 - 24
For equal roots,
Discriminant = 0
k2 - 24 = 0
k2 = 24
k = ±√24 = ±2√6
2(ii)
Answer
kx(x - 2) + 6 = 0or kx2 - 2kx + 6 = 0
Comparing this equation with ax2 + bx + c = 0, we get
a = k, b = - 2k and c = 6
Discriminant = b2 - 4ac
= ( - 2k)2 - 4 (k) (6)
= 4k2 - 24k
For equal roots,
b2 - 4ac = 0
4k2 - 24k = 0
4k (k - 6) = 0
Either 4k = 0
or k = 6 = 0
k = 0 or k = 6
However, if k = 0, then the equation will not have the terms 'x2' and 'x'.
Therefore, if this equation has two equal roots, k should be 6 only.
3
Answer
Length of mango grove will be 2l.
Area of mango grove = (2l) (l)= 2l2
2l2 = 800
l2 = 800/2 = 400
l2 - 400 =0
Comparing this equation with al2 + bl + c = 0, we get
a = 1, b = 0, c = 400
Discriminant = b2 - 4ac
Here, b2 - 4ac > 0
Therefore, the equation will have real roots. And hence, the desired rectangular mango grove can be designed.
l = ±20
However, length cannot be negative.
Therefore, breadth of mango grove = 20 m
Length of mango grove = 2 × 20 = 40 m
4
Answer
Let the age of one friend be x years.
then the age of the other friend will be (20 - x) years.
4 years ago,
Age of 2nd friend = (20 - x - 4) = (16 - x) years
A/q we get that,
(x - 4) (16 - x) = 48
- x2 + 20x - 112 = 0
x2 - 20x + 112 = 0
Comparing this equation with ax2 + bx + c = 0, we get
a = 1, b = -20 and c = 112
Discriminant = b2 - 4ac
= (-20)2 - 4 × 112
= 400 - 448 = -48
b2 - 4ac < 0
Therefore, there will be no real solution possible for the equations. Such type of condition doesn't exist.
5
Answer
Let the length and breadth of the park be l and b.Perimeter = 2 (l + b) = 80
l + b = 40
Or, b = 40 - l
Area = l×b = l(40 - l) = 40l - l240l - l2 = 400
l2 - 40l + 400 = 0
Comparing this equation with al2 + bl + c = 0, we get
a = 1, b = -40, c = 400
Discriminant = b2 - 4ac
(-40)2 - 4 × 400
= 1600 - 1600 = 0
b2 - 4ac = 0
Therefore, this equation has equal real roots. And hence, this situation is possible.
Root of this equation,l = -b/2a
l = (40)/2(1) = 40/2 = 20
Therefore, length of park, l = 20 m
And breadth of park, b = 40 - l = 40 - 20 = 20 m.