NCERT Solutions for Chapter 15 Probability Class 10 Maths
Book Solutions1
(i) Probability of an event E + Probability of the event ‘not E’ = ................
(ii) The probability of an event that cannot happen is ............... . Such an event is called .................
(iii) The probability of an event that is certain to happen is .............. . Such an event is called .................
(iv) The sum of the probabilities of all the elementary events of an experiment is .............. .
(v) The probability of an event is greater than or equal to .................. and less than or equal to ...............
Answer
(i) Probability of an event E + Probability of the event not E = 1.(ii) The probability of an event that cannot happen is 0. Such an event is called impossible event.
(iii) The probability of an event that is certain to happen is 1. Such an event is called sure or certain event.
(iv) The sum of the probabilities of all the elementary events of an experiment is 1.
(v) The probability of an event is greater than or equal to 0 and less than or equal to 1.
2
(i) A driver attempts to start a car. The car starts or does not start.
(ii) A player attempts to shoot a basketball. She/he shoots or misses the shot.
(iii) A trial is made to answer a true-false question. The answer is right or wrong.
(iv) A baby is born. It is a boy or a girl.
Answer
(i) Since, the car may or may not start, thus the outcomes are not equally likely.(ii) The player may shoot or miss the shot.
∴ The outcomes are not equally likely.
(iii) In advance it is known that the answer is to be either right or wrong.
∴ The outcomes right or wrong are equally likely to occur.
(iv) In advance it is known the newly born baby has to be either a boy or a girl.
∴ The outcomes either a boy or a girl are equally likely to occur.
3
Answer
Since on tossing a coin, the outcomes ‘head’ and ‘tail’ are equally likely, the result of tossing a coin is completely unpredictable and so it is a fair way.4
(A) 2/3
(B) − 1.5
(C) 15%
(D) 0.7
Answer
Since, the probability of an event cannot be negative,∴ (B) −1.5 cannot be the probability of an event.
5
Answer
∵ P(E) + P(not E)=1∴ 0.05 + P(not E)=1 ⇒ P(not E) = 1 − 0.05
= 0.95
Thus, probability of ‘not E’ = 0.95.
6
(i) an orange flavoured candy?
(ii) a lemon flavoured candy?
Answer
(i) Since, there are lemon flavoured candies only in the bag,∴ Taking out any orange flavoured candy is not possible.
⇒ Probability of taking out an orange flavoured candy = 0.
(ii) Also, probability of taking out a lemon flavoured candy = 1.
7
Answer
∴ Let the probability of 2 students having same birthday = P(SB) And the probability of 2 students not having the same birthday = P(nSB)∴ P(SB) + P(nSB)=1
⇒ P(SB) + 0.992 = 1
⇒ P(SB)=1 − 0.992 = 0.008
So, the required probability of 2 boys having the same birthday = 0.008.
8
(i) red?
(ii) not red?
Answer
Total number of balls = 3 + 5 = 8
∴ Number of all possible outcomes = 8
(i) For red balls: ä There are 3 red balls.
∴ Number of favourable outcomes = 3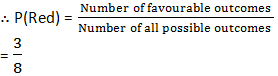

9
(i) red?
(ii) white?
(iii) not green?
Answer
Total number of marbles = 5 + 8 + 4 = 17
(i) For red marbles:
∵ Number of red marbles = 5
∴ Number of favourable outcomes = 5
∴ Probability of red marbles, P(red) = 5/17
(ii) For white balls:
∵ Number of white balls = 8
∴ Probability of white balls,
P(white)= 8/17
(iii) For not green balls:
∵ Number of white balls = 4
∴ Number of ‘not green’ balls = 17 − 4 = 13
i.e., Favourable outcomes = 13
P(not green) = 13/17
OR
Number of green marbles’ = 4
∴ Number of ‘not green balls’ = 17 − 4 = 13
⇒ Favourable outcomes = 13
∴ P(not green) = 13/17
10
Answer
Number of:
50 p coins = 100
Re 1 coins = 50
Rs 2 coins = 20
Rs 5 coins = 10
Total number of coins = 100 + 50 + 20 + 5 = 180
(i) For a 50 p coin:
Favourable events = 100
∴ P(50 p) = 100/180 = 5/9
(ii) For not a Rs 5 coin:
∵ Number of Rs 5 coins = 10
∴ Number of ‘not Rs 5’ coins = 180 − 10 = 170
⇒ Favourable outcomes = 170
∴ P(not 5 rupee coin) = 170/180 = 17/18.
11
Answer
Number of:Male fishes = 5
Female fishes = 8
∴ Total number of fishes = 5 + 8 = 13
⇒ Total number of outcomes = 13
For a male fish:
Number of favourable outcomes = 5
∴ P(male fish) = 5/13.
12
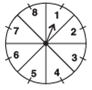
(i) 8 ?
(ii) an odd number?
(iii) a number greater than 2?
(iv) a number less than 9?
Answer
Total numbers marked = 8
(i) When pointer points at 8:
Total number of outcomes = 8
Number of favourable outcomes = 1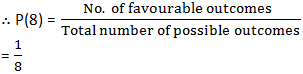
(ii) When pointer points at an odd number:
Number of odd numbers from 1 to 8 = 4
[∵ Odd numbers are 1, 3, 5 and 7]
⇒ Number of favourable outcomes = 4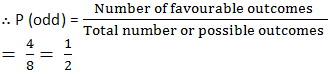
(iii) When pointer points at a number greater than 2:
Number of numbers greater than 2 = 6
[∴ The numbers 2, 3, 4, 5, 6, 7 and 8 are greater than 2]
⇒ Number of favourable outcomes = 6![]()
13
(i) a prime number;
(ii) a number lying between 2 and 6;
(iii) an odd number.
Answer
Since, numbers on a die are 1, 2, 3, 4, 5, and 6.
∴ Number of total outcomes = 6
(i) For prime numbers:
Since 2, 3, and 5 are prime number,
∴ Favourable outcomes = 3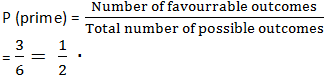
(ii) For a number lying between 2 and 6:
Since the numbers between 2 and 6 are 3, 4 and 5
∴ Favourable outcomes = 3![]()
(iii) For an odd number:
Since 1, 3 and 5 are odd numbers.
⇒ Favourable outcomes = 3![]()
14
(i) a king of red colour
(ii) a face card
(iii) a red face card
(iv) the jack of hearts
(v) a spade
(vi) the queen of diamonds
Answer
Number of cards in deck = 52
∴ Total number of possible outcomes = 52
(i) For a king of red colour:
∵ Number of red colour kings = 2
[∵ Kings of diamond and heart are red]
∴ Number of favourable outcomes = 2![]()
(ii) For a face card:
∵ 4 kings, 4 queens and 4 jacks are face cards
∴ Number of face cards = 12
⇒ Number of favourable outcomes = 12![]()
(iii) For a red face card:
Since, cards of diamond and heart are red
∴ There are [2 kings, 2 queens, 2 jacks] 6 cards are red
⇒ Favourable outcomes = 6![]()
(iv) For a jack of hearts:
Since, there is only 1 jack of hearts.
∴ Number of favourable outcomes = 1![]()
(v) For a spade:
∵There are 13 spades in a pack of 52 cards:
∴ Favourable outcomes are 13.![]()
(vi) For the queen of diamonds:
∵ There is only one queen of diamond.
∴ Number of favourable outcomes.![]()
15
(i) What is the probability that the card is the queen?
(ii) If the queen is drawn and put aside, what is the probability that the second card picked up is
(a) an ace?
(b) a queen?
Answer
We have five cards.
∴ All possible outcomes = 5
(i) For a queen:
∵ Number of queens = 1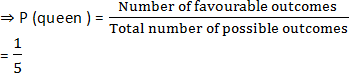
(ii) The queen is drawn and put aside,
∴ Only 5 − 1 = 4 cards are left,
⇒ All possible outcomes = 4
(a) For an ace:
∵ There is only one ace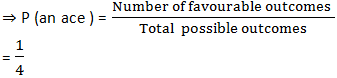
(b) For a queen:
Since, the only queen has already been put aside.
∴ Number of possible outcomes = 0
16
Answer
We have
Number of good pens = 132
Number of defective pens = 1 2
∴ Total number of pens = 132 + 12 = 144
For good pens:
∵ There are 132 good pens
∴ Number of favourable outcomes = 132![]()
17
(ii) Suppose the bulb drawn in (i) is not defective and is not replaced. Now one bulb is drawn at random from the rest. What is the probability that this bulb is not defective?
Answer
Since, there are 20 bulbs in the lot.
∴ Total number of possible outcomes = 20
(i) ∵ Number defective bulbs = 4
i.e., Favourable outcomes = 4![]()
(ii) ∵ The bulb drawn above is not included in the lot.
∴ Remaining number of bulbs = 20 − 1 = 19.
⇒ Total number of possible outcomes = 19.
∵ Number of bulbs which are not defective = 19 − 4 = 15
⇒ Favourable number of outcomes = 15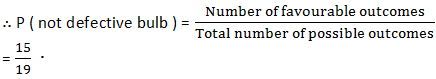
18
Answer
We have:
Total number of discs = 90
∴ Total number of possible outcomes = 90
(i) For a two-digit number:
Since the two-digit numbers are 10, 11, 12, ....., 90.
∴ Number of two-digit numbers = 90 − 9 = 81
[∵ 1, 2, 3, 4, 5, 6, 7, 8, and 9 are 1-digit numbers]
⇒ Number of favourable outcomes = 81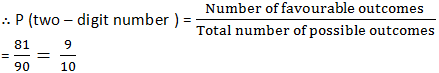
(ii) For a perfect square:
Perfect squares from 1 to 90 are 1, 4, 9, 16, 25, 36, 49, 64, and 81
∴ Number of perfect numbers = 9
⇒ Number of favourable outcomes = 9![]()
(iii) For a number divisible by 5:
Numbers divisible by 5 [from 1 to 90] are: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85, 90
i.e. There are 18 number (1 to 90) which are divisible by 5.
∴ Number of favourable outcomes = 18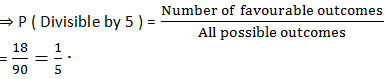
19
The die is thrown once. What is the probability of getting
(i) A? and (ii) D?
Answer
Since there are six faces of the given die and these faces are marked with letters![]()
∴ Total number of letters = 6
⇒ Number of possible outcomes = 6
(i) For the letter A
∵ Two faces are having the letter A.
∴ Number of favourable outcomes = 2![]()
(ii) For the letter D:
∵ Number of D’s = 1
∴ Number of possible outcomes = 1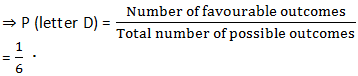
20
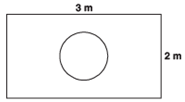
Answer
Here, Area of the rectangle = 3 m × 2 m = 6 m2
And, the area of the circle = πr2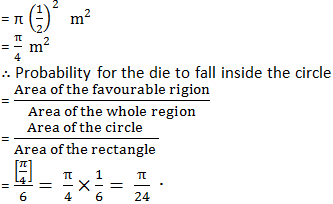
21
(i) She will buy it?
(ii) She will not buy it?
Answer
Total number of ball pens = 144
⇒ All possible outcomes = 144
(i) Since there are 20 defective pens
∴ Number of good pens 144 − 20 = 124
⇒ Number of favourable outcomes = 124
∴ Probability that she will buy it![]()
(ii) Probability that she will not buy it
=1 − [Probability that she will buy it]
22
(i)Complete the following table:
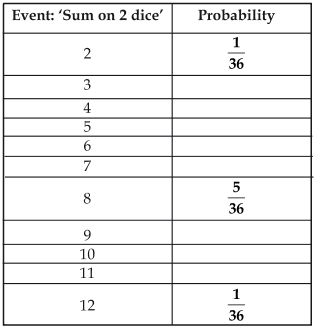
(ii) A student argues that there are 11 possible outcomes 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 and 12. Therefore, each of them has a probability 1/11. Do you agree with this argument? Justify your answer.
Answer
∵ The two dice are thrown together.
∴ Following are the possible outcomes:
(1, 1); (1, 2); (1, 3); (1, 4); (1, 5); (1, 6).
(2, 1); (2, 2); (2, 3); (2, 4); (2, 5); (2, 6).
(3, 1); (3, 2); (3, 3); (3, 4); (3, 5); (3, 6).
(4, 1); (4, 2); (4, 3); (4, 4); (4, 5); (4, 6).
(5, 1); (5, 2); (5, 3); (5, 4); (5, 5); (5, 6).
(6, 1); (6, 2); (6, 3); (6, 4); (6, 5); (6, 6).
⇒ Number of all possible outcomes is 6 × 6 = 36.
(i) Let the required probability be P(E).
(a) ∵ The sum on two dice is 3 for: (1, 2) and (2, 1)
∴ Favourable outcomes = 2
⇒ P(E) = 2/36
(b) ∵ The sum on two dice is 4 for: (1, 3), (2, 2) and (3, 1).
∴ Number of favourable outcomes = 3
⇒ P(2) = 3/36
(c) ∵ The sum on two dice is 5 for:
(1, 4), (2, 3), (3, 2) and (4, 1)
∴ Number of favourable outcomes = 4
⇒ P(E) = 4/36
(d) ∵ The sum on two dice is 6 for:
(1, 5), (2, 4), (3, 3), (4, 2) and (5, 1)
∴ Number favourable outcomes = 5
⇒ P(E) = 5/36
(e) ∵ The sum on two dice is 7 for:
(1, 6), (2, 5), (3, 4), (4, 3), (5, 2) and (6, 1)
∴ Number of favourable outcomes = 6
⇒ P(E) = 6/36
(f) ∵ The sum on two dice is 9 for:
(3, 6), (4, 5), (5, 4) and (6, 3)
∴ Number of favourable outcome = 4
⇒ P(E) = 4/36
(g) ∵ The sum on two dice is 10 for:
(4, 6), (5, 5), (6, 4)
∴ Number of favourable outcomes = 3
⇒ P(E)= 3/36
(h) The sum on two dice is 11 for: (5, 6) and (6, 5)
∴ Number of favourable outcomes = 2
⇒ P(E) = 2/36
Thus, the complete table is as under: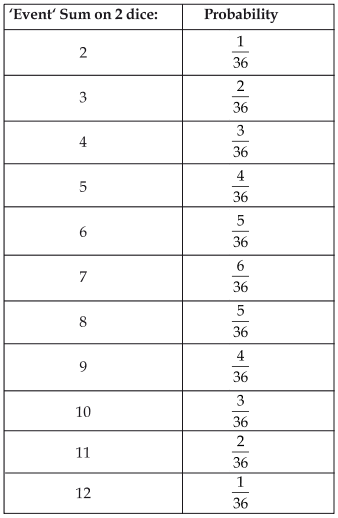
(ii) No. The number of all possible outcomes is 36 and not 11.
∴ The argument is not correct.
23
Answer
Let T denotes the tail and H denotes the head.
∴ All the possible outcomes are:
H H H, H H T, H T T, T T T, T T H, T H T, T T H, H T H
∴ Number of all possible outcomes = 8
Let the event that Hanif will lose the game be denoted by E.
∴ Favourable events are:
H H T, H T H, T H H, T H T , T T H, H T T
⇒ Number of favourable outcomes = 3![]()
24
(i) 5 will not come up either time?
(ii) 5 will come up at least once?
[Hint: Throwing a die twice and throwing two dice simultaneously are treated as the same experiment.]
Answer
Since, throwing a die twice or throwing two dice simultaneously is the same.
∴ All possible outcomes are:
(1, 1); (1, 2); (1, 3); (1, 4); (1, 5); (1, 6)
(2, 1); (2, 2); (2, 3); (2, 4); (2, 5); (2, 6)
(3, 1); (3, 2); (3, 3); (3, 4); (3, 5); (3, 6)
(4, 1); (4, 2); (4, 3); (4, 4); (4, 5); (4, 6)
(5, 1); (5, 2); (5, 3); (5, 4); (5, 5); (5, 6)
(6, 1); (6, 2); (6, 3); (6, 4); (6, 5); (6, 6)
∴ All possible outcomes = 36
(i) Let E be the event that 5 does not come up either time, then
The favourable outcomes are [36 − (5 + 6)] = 25
⇒ P(E) = 25/36
(ii) Let N be the event that 5 will come up at least once, then Number of favourable outcomes = 5 + 6 = 11
∴ P(N) = 11/36
25
(i) If two coins are tossed simultaneously there are three possible outcomes—two heads, two tails or one of each. Therefore, for each of these outcomes, the probability is 1/3.
(ii) If a die is thrown, there are two possible outcomes—an odd number or an even number.
Therefore, the probability of getting an odd number is 1/2.
Answer


1
(i) the same day?
(ii) consecutive days?
(iii) different days?
Answer
Here, the number of all the possible outcomes
= 5 × 5 = 25
(i) For both customers visiting same day:
Number of favourable outcomes = 5
∴ Required probability = 1/25 = 1/5
(ii) For both the customers visiting on consecutive days:
Number of outcomes are: (Tue., Wed.), (Wed., Thu.), (Thu., Fri.), (Fri., Sat.), (Sat., Fri.), (Wed., Tue.), (Thu., Wed.), (Fri., Thu.)
∴ Number of favourable outcomes = 8
⇒ Required probability = 8/25
(iii) For both the customers visiting on different days: We have probability for both visiting same day = 1/5
∴ Probability for both visiting on different days
= 1 − [Probability for both visiting on the same day]![]()
2
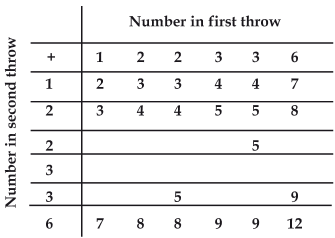
What is the probability that the total score is
(i) even?
(ii) 6?
(iii) at least 6?
Answer
The completed table is as under: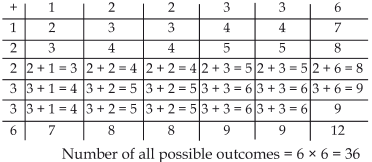

3
Answer
Let the number of blue balls in the bag be x.∴ Total number of balls = x + 5
Number of possible outcomes = (x + 5).
For a blue ball favourable outcomes = x
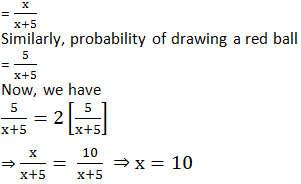
Thus the required number of blue balls = 10.
4
If 6 more black balls are put in the box, the probability of drawing a black ball is now double of what it was before. Find x.
Answer
∵ The total number of balls in the box = 12∴ Number of possible outcomes = 12
Case-I
For drawing a black ball
Number of favourable outcomes = x
∴ Probability of getting a black ball = x/12.
Case-II
When 6 more black balls are added
Now, the total number of balls
= 12 + 6
= 18
⇒ Number of possible outcomes = 18
Since, the number of black balls now =(x + 6).
⇒ Number of favourable outcomes = (x + 6)
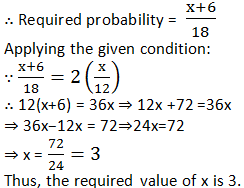
5
Answer
∵ There are 24 marbles in the jar.∴ Number of possible outcomes = 24.
Let there are x blue marbles in the jar.
∴ Number of green marbles = 24 − x
⇒ Favourable outcomes = (24 − x)
∴ Required probability for drawing a green marble
