NCERT Solutions for Chapter 2 Polynomials Class 10 Maths
Book Solutions1
The graphs of y = p (x) are given in the figure given below, for some polynomials p (x). Find the number of zeroes of p (x), in each case.

Answer
(i) The given graph is parallel to x-axis. It does not intersect the x-axis.∴ It has no zeroes.
(ii) The given graph intersects the x-axis at one point only.
∴It has one zero.
(iii) The given graph intersects the x-axis at three points.
∴ It has three zeroes.
(iv) The given graph intersects the x-axis at two points.
∴It has two zeroes.
(v) The given graph intersects the x-axis at four points.
∴ It has four zeroes.
(vi) The given graph meets the x-axis at three points.
∴ It has three zeroes.
1(i)
(i) x2 - 2x - 8
Answer
(i) x2 - 2x - 8
We have p (x) = x2 - 2x - 8
= x2 + 2x - 4x - 8 = x (x + 2) - 4 (x + 2)
= (x - 4) (x + 2)
For p (x) = 0, we have
(x - 4) (x + 2) = 0
Either x - 4 = 0 ⇒ x = 4
or x + 2 = 0 ⇒ x = - 2
∴ The zeroes of x2 - 2x - 8 are 4 and - 2.

Thus, relationship between zeroes and the coefficients in x2 - 2x - 8 is verified.
1(ii)
Answer
(ii) 4s2 - 4s + 1
We have p (s) = 4s2 - 4s + 1
= 4s2 - 2s - 2s + 1 = 2s (2s - 1) - 1 (2s - 1)
= (2s - 1) (2s - 1)
For p (s) = 0, we have,
(2s - 1) = 0 ⇒ s = 1/2
∴ The zeroes of 4s2 - 4s + 1 are 1/2 and 1/2
Now,

Thus, the relationship between the zeroes and coefficients in the polynomial 4s2 - 4s + 1 is verified.
1(iii)
Answer
(iii) 6x2 - 3 - 7x
We have
p (x) = 6x2 - 3 - 7x
= 6x2 - 7x - 3
= 6x2 - 9x + 2x - 3
= 3x (2x - 3) + 1 (2x - 3)
= (3x + 1) (2x - 3)
For p (x) = 0, we have,
Either (3x+1) = 0

Thus, the relationship between the zeroes and the coefficients in the polynomial 6x2 - 3 - 7x is verified.
1(iv)
Answer
(iv) 4u2 + 8u
We have, f(u) = 4u2 + 8u = 4u (u + 2)
For f (u) = 0,
Either 4u = 0 ⇒ u = 0
or u + 2 = 0 ⇒ u = - 2
∴ The zeroes of 4u2 + 8u are 0 and - 2.
Now, 4u2 + 8u can be written as 4u2 + 8u + 0.

Thus, the relationship between the zeroes and the coefficients in the polynomial 4u2 + 8u is verified.
1(v)
Answer
(v) t2 - 15
We have,
f (t) = t2 - 15 = (t)2 - (√15)2
( t+√15) = (t- √15)
For f (t) = 0, we have
Either ( t+√15) = 0 ⇒ t = -√15
or (t- √15) = 0 ⇒ t = √15
∴ The zeroes of t2 - 15 are -√15 and √15.
Now, we can write t2 - 15 as t2 + 0t - 15.

Thus, the relationship between the zeroes and the coefficients in the polynomial t2 - 15 is verified.
1(vi)
Answer
(vi) 3x2 – x – 4
We have, f (x) = 3x2 - x - 4 = 3x2 + 3x - 4x - 4
= 3x (x + 1) - 4 (x + 1)
= (x + 1) (3x - 4)
For f (x) = 0 ⇒ (x + 1) (3x - 4) = 0
Either (x + 1) = 0 ⇒ x = - 1
or 3x - 4 = 0 ⇒ x = 4/3
∴The zeroes of 3x2 - x - 4 are 1 and
Now,

Thus, the relationship between the zeroes and the coefficients in 3x2 - x - 4 is verified.
2(i)
Find a quadratic polynomial each with the given numbers as sum and product of its zeroes respectively:
(i) 1/4, -1
Answer
Note: A quadratic polynomial whose zeroes are α and β is given by
p (x) = {x2 -(α + β) x + αβ}
i.e., p (x) = {x2 - (sum of the zeroes) x + (product of the zeroes)}
(i) Sum of the zeroes, (α + β) =
Product of the zeroes, ab = - 1
∴ The required quadratic polynomial is
x2 - (α + β) x + ab
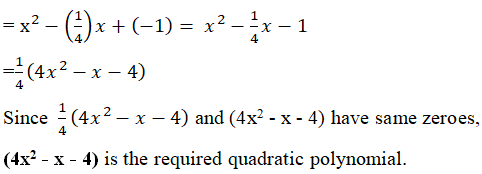
2(ii)
Answer
(ii) Sum of the zeroes, (α + β) = √2
Product of zeroes, αβ = 1/3
∴The required quadratic polynomial is
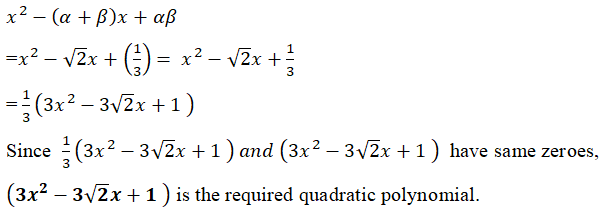
2(iii)
Answer
(iii) Since, sum of zeroes, (α + β) = 0Product of zeroes, αβ = √5
∴ The required quadratic polynomial is
x2 - (α + β) x + αβ
= x2 - (0) x + √5
= x2 + √5
2(iv)
Answer
(iv) Since, sum of the zeroes, (α + β) = 1Product of the zeroes = 1
∴The required quadratic polynomial is
x2 - (α + β) x + αβ
= x2 - (1) x + 1
= x2 - x + 1
2(v)
Answer
(v) Since, sum of zeroes, (α+β) = -1/4
Product of zeroes, αβ = 1/4
∴ The required quadratic polynomial
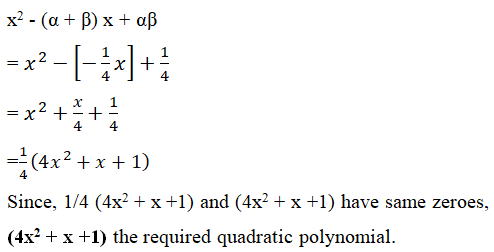
2(vi)
Answer
(vi) Since, sum of the zeroes, (α + β) = 4Product of the zeroes, αβ = 1
∴ The required quadratic polynomial is
= x2 - (α + β) x + αβ
= x2 - (4) x + 1
= x2 - 4x + 1
1
(i) p (x) = x3 - 3x2 + 5x - 3, g (x) = x2 - 2
(ii) p (x) = x4 - 3x2 + 4x + 5, g (x) = x2 + 1 - x
(iii) p (x) = x4 - 5x + 6, g (x) = 2 - x2
Answer
(i) Here, dividend p (x) = x3 - 3x2 + 5x - 3
divisor g (x) = x2 - 2
∴ We have
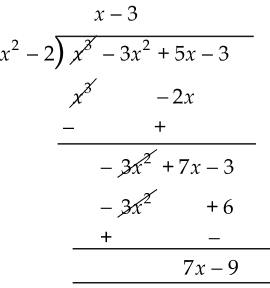
Thus, the quotient = (x - 3) and remainder = (7x - 9)
(ii) Here, dividend p (x) = x4 - 3x2 + 4x + 5 = x4 + 0x3 - 3x2 + 4x + 5
and divisor g (x) = x2 + 1 - x = x2 - x + 1
∴ We have
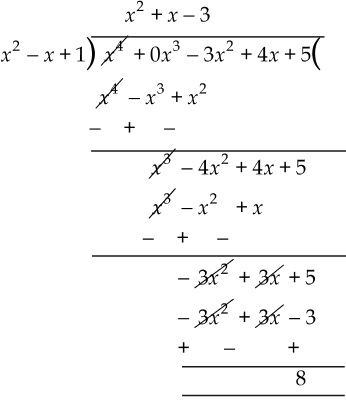
Thus, the quotient is (x2 + x - 3) and remainder = 8
(iii) Here, dividend, p (x) = x4 - 5x + 6 = x4 + 0x3 +0x2- 5x + 6
and divisor, g (x) = 2 - x2 = - x2 + 2
∴ We have
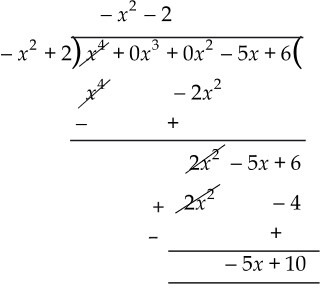
Thus, the quotient = –x2 – 2 and remainder = –5x + 10
2
Check whether the first polynomial is a factor of the second polynomial by dividing the second polynomial by the first polynomial:
(i) t2 – 3, 2t4 + 3t3 – 2t2 – 9t – 12
(ii) x2 + 3x + 1, 3x4 + 5x3 – 7x2 + 2x + 2
(iii) x3 – 3x + 1, x5 – 4x3 + x2 + 3x + 1
Answer
(i) Dividing 2t4 + 3t3 - 2t2 - 9t - 12 by t2 - 3, we have:
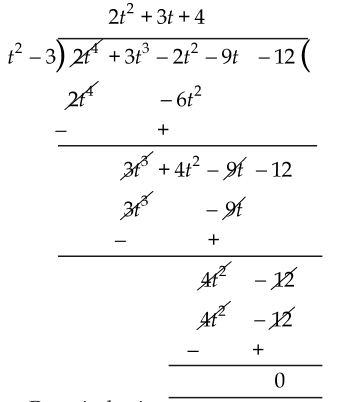
∵ Remainder = 0
∴ (t2 - 3) is a factor of 2t4 + 3t3 - 2t2 - 9t - 12.
(ii) Dividing 3x4 + 5x3 - 7x2 + 2x + 2 by x2 + 3x + 1, we have:
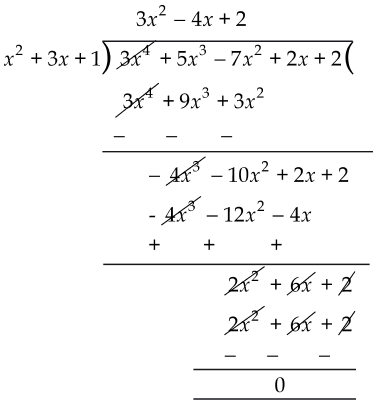
∵ Remainder = 0.
∴ x2 + 3x + 1 is a factor of 3x4 + 5x3 - 7x2 + 2x + 2.
(iii) Dividing x5 - 4x3 + x2 + 3x + 1 by x3 - 3x + 1, we get:
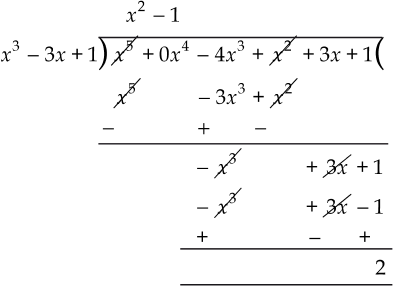
∴ The remainder = 2, i.e., remainder ≠ 0
∴ x3 - 3x + 1 is not a factor of x5 - 4x3 + x2 + 3x + 1.
3
Obtain all other zeroes of 3x4 + 6x3 - 2x2 - 10x - 5, if two of its zeroes ![]()
Answer
We have p (x) = 3x4 + 6x3 - 2x2 - 10x - 5
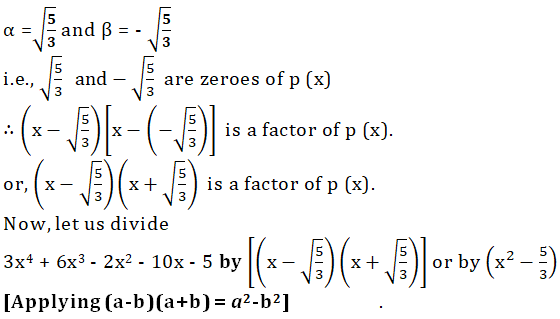
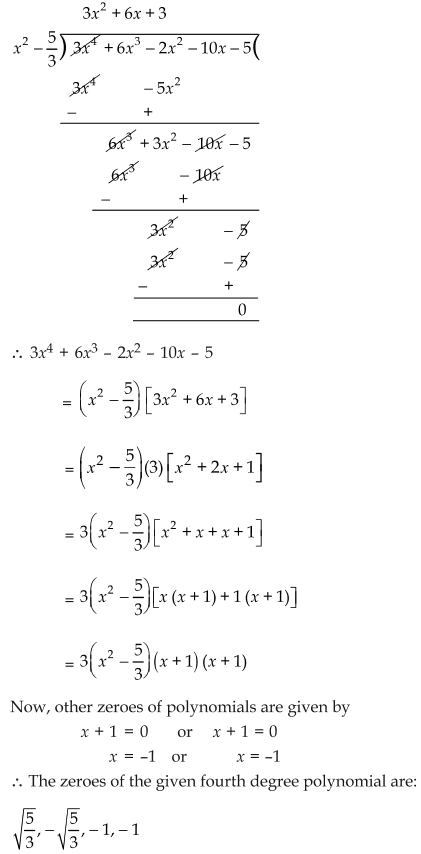
4
Answer
Here,
Dividend p (x) = x3 - 3x2 + x + 2
Divisor = g (x)
Quotient = (x - 2)
Remainder = (-2x + 4)
Since,
(Quotient × Divisor) + Remainder = Dividend
∴ [(x − 2) × g (x)] + [(−2x + 4)] = x3 − 3x2 + x + 2
⇒ (x − 2) × g (x)= x3 − 3x2 + x + 2 − (−2x + 4)
= x3 − 3x2 + x + 2 + 2x −4
= x3 - 3x2 + 3x - 2
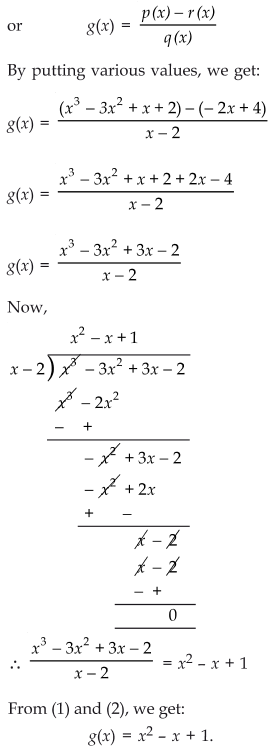
5
(i) deg p (x) = deg q (x)
(ii) deg q (x) = deg r (x)
(iii) deg r (x) = 0
Answer
We have
(i) p (x) = 3x2 - 6x + 27
g (x) = 3
q (x) = x2 - 2x + 9
r (x) = 0
p (x)= q (x) × g (x) + r (x).
(ii) p (x)= 2x3 − 2x2 + 2x + 3
g (x) = 2x2 − 1
q (x) = x − 1
r (x) = 3x + 2
⇒ p (x)= q (x) × g (x) + r (x)
(iii) p (x) = 2x3 − 4x2 + x + 4
g (x) = 2x2 + 1
q (x)= x − 2
r (x) = 6
⇒ p (x)= q (x) × g (x) + r (x)
1(i)
Verify that the numbers given alongside of the cubic polynomials below are their zeroes. Also verify the relationship between the zeroes and the coefficients in each case:
(i) 2x3 + x2 - 5x + 2; 1/2, 1 , -2
Answer
Let p (x) = 2x3 + x2 - 5x + 2
Comparing with ax3 + bx2 +cx+d
a = 2, b = 1, c = -5, d = 2
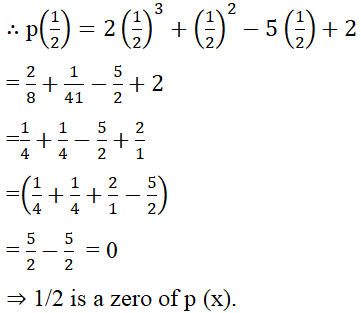
Again,
p (1) = 2 (1)3 + (1)2 - 5 (1) + 2
= 2 + 1 - 5 + 2
= (2 + 2 + 1) - 5
= 5 - 5 = 0
⇒ 1 is a zero of p (x).
Also p (- 2) = 2 (- 2)3 + (- 2)2 - 5 (- 2) + 2
= 2(- 8) + (4) + 10 + 2
= - 16 + 4 + 10 + 2
= - 16 + 16 = 0
⇒ -2 is a zero of p (x).
Relationship
∵ p (x) = 2x3 + x2 - 5x + 2
∴ Comparing it with ax3 + bx2 + cx + d, we have :
a = 2, b = 1, c = - 5 and d = 2
Also 1/2 , 1 and - 2 are the zeroes of p (x)
Let α = 1/2 , β = 1 and γ = - 2

Thus, the relationship between the co-efficients and the zeroes of p (x) is verified.
1(ii)
Answer
(ii) Here, p (x) = x3 - 4x2 + 5x - 2
∴ p (2) = (2)3 - 4 (2)2 + 5 (2) - 2
= 8 - 16 + 10 - 2
= 18 - 18 = 0
⇒ 2 is a zero of p (x)
Again p (1) = (1)3 - 4 (1)2 + 5 (1) - 2
= 1 - 4 + 5 - 2
= 6 - 6 = 0
⇒ 1 is a zero of p (x).
∴ 2, 1, 1 are zeroes of p (x).
Now,
Comparing p (x) = x3 - 4x2 + 5x - 2 with ax3 + bx2 + cx + d = 0, we have
a = 1, b = -4, c = 5 and d = -2
∵ 2, 1, and 1 are the zeroes of p (x)
∴ Let α = 2
β = 1
γ = 1
Relationship, α + β + γ = 2 + 1 + 1 = 4

Thus, the relationship between the zeroes and the co-efficients of p (x) is verified.
2
Answer
Let the required cubic polynomial be ax3 + bx2 + cx + d and its zeroes be a, b and g.
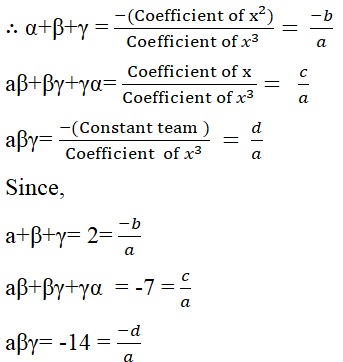
If a = 1, then -b/a = 2 ⇒ b = - 2
c/a = - 7 ⇒ c = - 7
-d/a = - 14 ⇒ d = 14
∴ The required cubic polynomial
= 1x3 + (-2)x2 + (-7) x + 14
= x3 - 2x2 - 7x + 14
3
Answer
We have
p (x) = x3 - 3x2 + x + 1
Comparing it with ax3 + bx2 + cx + d.
We have
a = 1, b = - 3, c = 1 and d = 1
∵ It is given that (a - b), a and (a + b) are the zeroes of the polynomial.
∴ Let, α = (a - b)
β = a
and γ = (a + b)
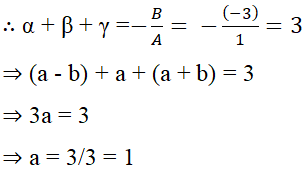
Again, αβγ = -d/a = -1
⇒ (a - b) × a × (a + b) = - 1
⇒ (1 - b) × 1 × (1 + b) = - 1 [∵ a = 1, proved above]
⇒ 1 - b2 = - 1
⇒ b2 = 1 + 1 = 2
⇒ b = ± √2
Thus, a = 1 and b = ±√2
4
Answer
Here, p (x) = x4 - 6x3 - 26x2 + 138x - 35.
∵ Two of the zeroes of p (x) are : 2±
∴[x-(2+√3)] [x-(2-√3)]
or, [(x-2)-√3] [(x-2)+√3]
or, (x - 2)2 - (√3)2
or, (x2 + 4 - 4x) - 3
or, x2 - 4x + 1 is a factor of p (x).
Now, dividing p (x) by x2 - 4x + 1 we have,

5
Answer
Given that if the polynomial, x4 - 6x3 + 16x2 - 25x + 10 is divided by another polynomial, x2 - 2x + k, then remainder comes out is (x+a).
So, we divide x4 - 6x3 + 16x2 - 25x + 10 by x2 - 2x + k to find quotient and remainder.
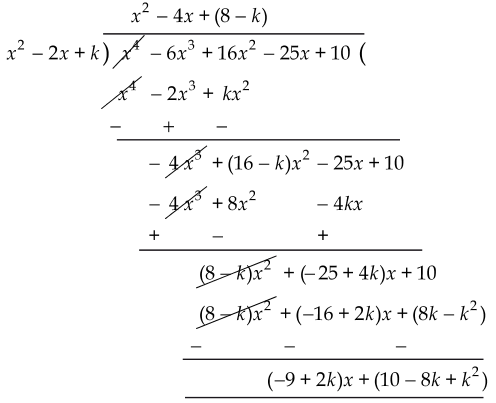
∵ Remainder = (2k - 9)x - k (8 - k) + 10
But the remainder = x + α
Applying the division algorithm to the polynomials x4 - 6x3 + 16x2 - 25x + 10 and comparing the like coefficients,
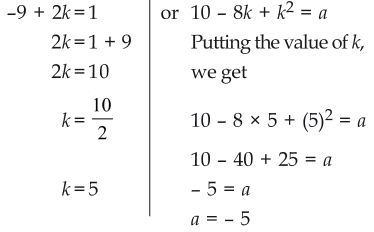
Thus, k = 5 and α = -5