NCERT Solutions for Ch 5 Parallel and Intersecting Lines Class 7 Maths
Book Solutions1
Answer
Some pairs of lines meet at a point on the paper, forming intersecting lines. Others do not meet within the paper. If extended beyond the paper, some non-meeting lines may intersect outside the paper, while others, if parallel, will never meet.
Let us observe what happens when two lines intersect.
2
Answer
When two lines intersect, they form four angles.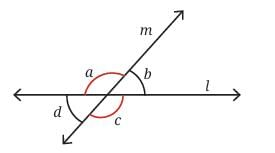
3
Answer
No, two straight lines can only intersect at one point. If they are parallel, they never intersect. But if two lines appear to intersect at more than one point, it means they are the same.4
Draw two lines on a plain sheet of paper so that they intersect. Measure the four angles formed with a protractor. Draw four such pairs of intersecting lines and measure the angles formed at the points of intersection.
Q: What patterns do you observe among these angles?
Answer
The patterns we observed among these angles are:Vertically opposite angles are equal:
For example, in the figure, ∠a = ∠c and ∠b = ∠d.
Linear pairs add up to 180°:
Adjacent angles like ∠a + ∠b or ∠b + ∠c form a straight angle, which means their sum is always 180°.
These patterns are true for any pair of intersecting lines and form the basis of angle relationships in geometry.
5
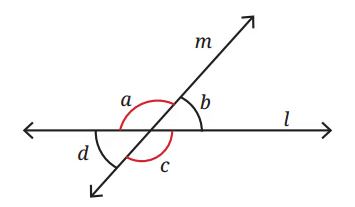
Answer
∠b = 180° - ∠a= 180° - 120° = 60° (linear pair).
∠c = ∠a = 120° (vertically opposite).
∠d = ∠b = 60° (vertically opposite).
6
Answer
Yes. When two lines intersect, they form four angles at a point of intersection. The angles directly opposite each other at this point are called vertically opposite angles, and they are always equal in measure.7
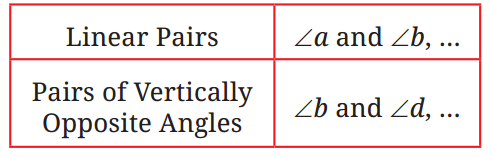
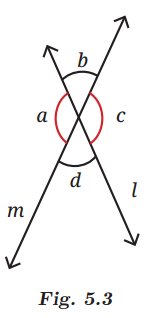
Answer
Linear Pairs: These are angles that are adjacent and form a straight line (add up to 180°).
- ∠a and ∠b
- ∠b and ∠c
- ∠c and ∠d
- ∠d and ∠a
Vertically Opposite Angles: These are angles that are opposite each other when two lines intersect (they are equal).
- ∠b and ∠d (they are opposite each other at the intersection).
- ∠a and ∠c (they are opposite each other at the intersection).
8
Observe given figure below and describe the way the line segments meet or cross each other in each case, with appropriate mathematical words (a point, an endpoint, the midpoint, meet, intersect) and the degree measure of each angle.
For example, line segments FG and FH meet at the endpoint F at an angle 115.3°.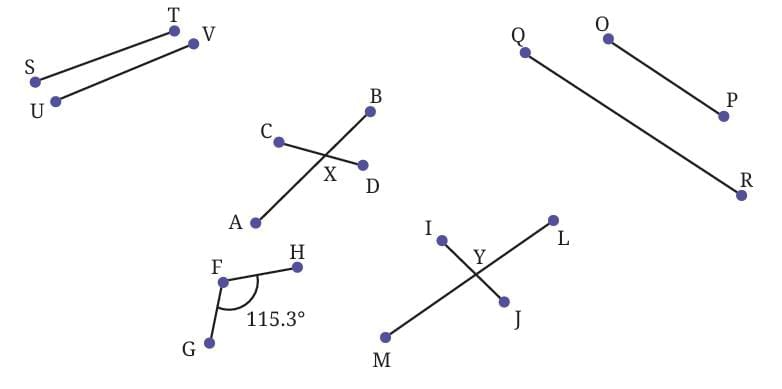
Are line segments ST and UV likely to meet if they are extended?
Are line segments OP and QR likely to meet if they are extended?
Answer
If the lines are not parallel, they will likely intersect at some point. Thus, line segments ST and UV are likely to meet when extended, as they are not parallel.
If two lines are parallel, they will never meet, regardless of how far they are extended. Thus, line segments OP and QR didn’t meet when extended, as they are parallel.
9
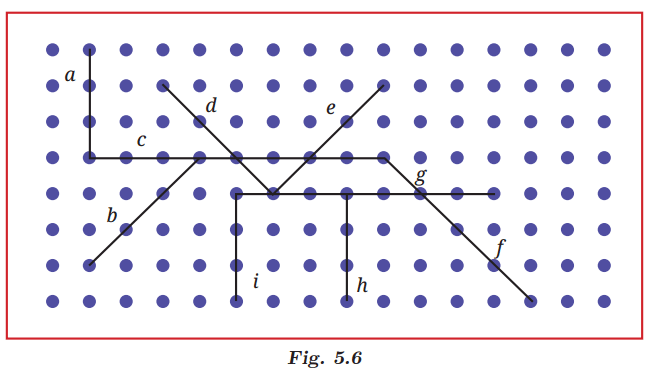
Answer
Two lines are said to be parallel when they do not meet at any point.Here, lines a, i, and h are parallel to each other;
Line c is parallel to line g;
Line d is parallel to line f;
Line e is parallel to line b.
10
Take a plain square sheet of paper (use a newspaper for this activity). 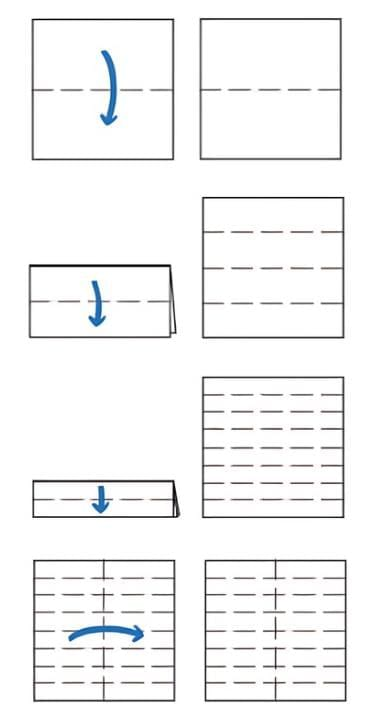
Q1: How would you describe the opposite edges of the sheet? They are __________to each other.
Answer
The opposite edges of the sheet are parallel to each other.11
Answer
The adjacent edges are perpendicular to each other. They meet at a point and form right angles (90°).12
Answer
The two original top/bottom edges and the new horizontal fold.13
Answer
After folding horizontally, there are two parallel lines (the new crease and one horizontal edge). The new line segment is parallel to the horizontal edges and perpendicular to the vertical sides.14
Answer
After another horizontal fold, there are 5 parallel lines (the two original edges plus the three horizontal folds).15
Answer
Doing it once more (a third horizontal fold) would result in 9 parallel lines (2 original edges + 7 folds).
The pattern relates to powers of 2; after n folds, we have ![]() fold lines, plus the 2 original edges for
fold lines, plus the 2 original edges for ![]() total parallel lines (starting from n =1 fold).
total parallel lines (starting from n =1 fold).
We can check if the pattern continues.
16
Answer
The new vertical line is perpendicular to the previous horizontal lines.17
Answer
This requires performing the activity. It is possible to create such a fold (e.g., by folding an edge onto the diagonal or folding the paper in half parallel to the first diagonal fold).18
• Take a square sheet of paper, fold it in the middle and unfold it.
• Fold the edges towards the centre line and unfold them.
• Fold the top right and bottom left corners onto the creased line to create triangles.
• The triangles should not cross the crease lines.
• Are a, b and c parallel to p, q and r respectively? Why or why not?
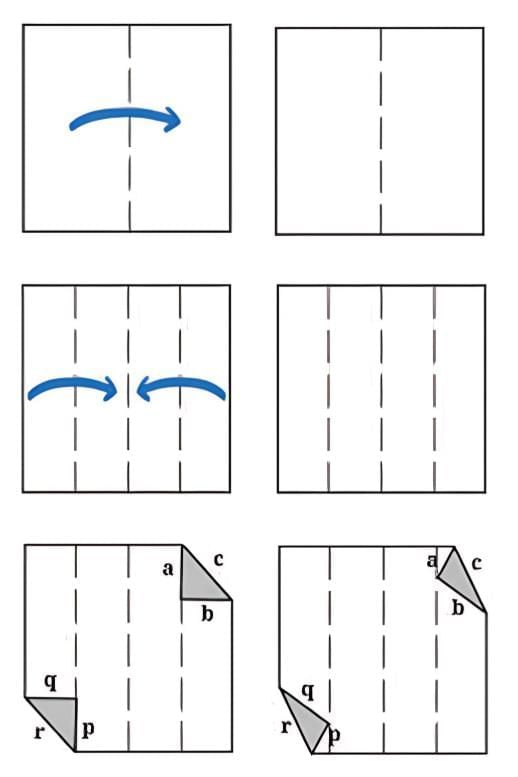
Answer
Do it Yourself.19
Answer
Do it Yourself.20
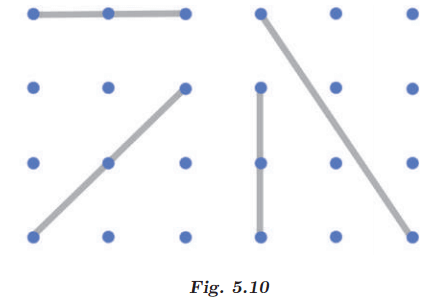
(a) How did you spot the perpendicular lines?
(b) How did you spot the parallel lines?
Answer
(a) To spot perpendicular lines in a geometric figure, observe if lines intersect at a 90° angle.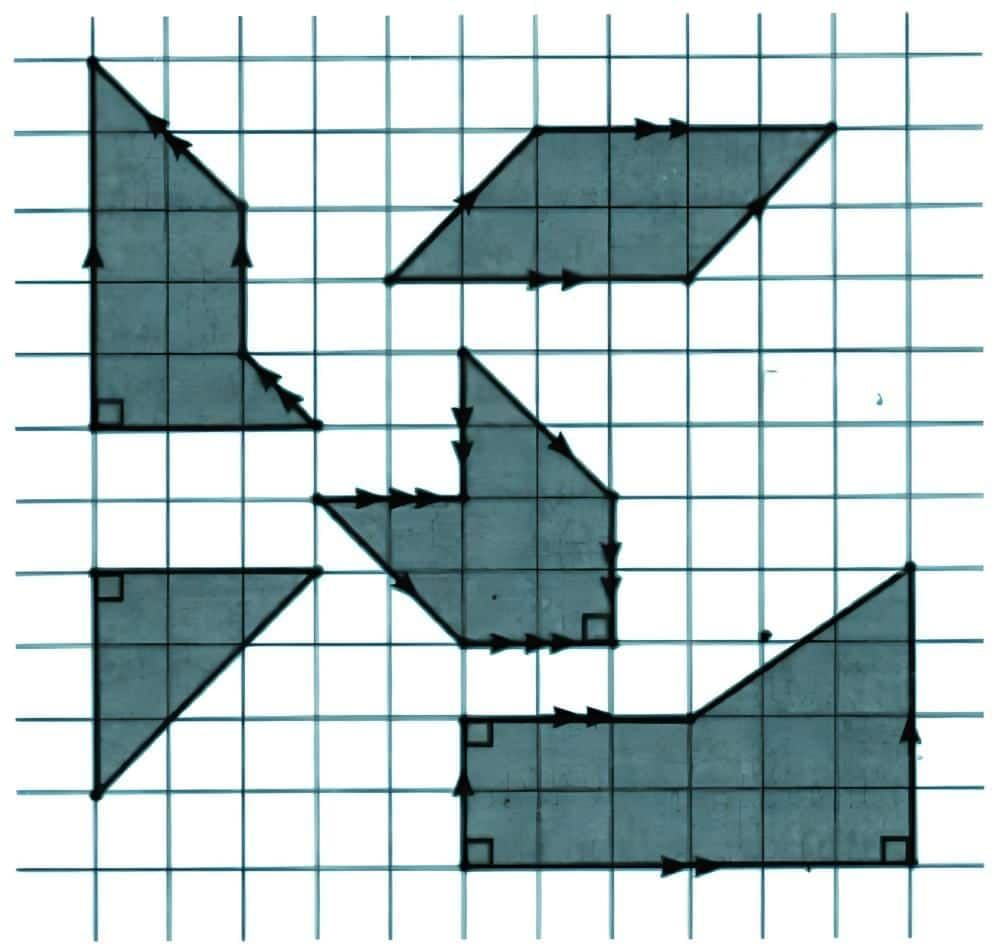
(b) To spot parallel lines in a geometric figure, observe if lines never intersect at any point.
21
Answer
Do it yourself.22
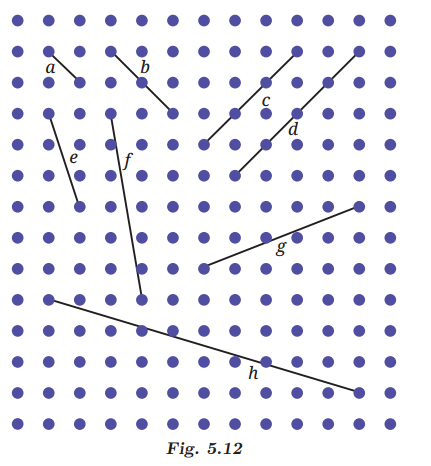
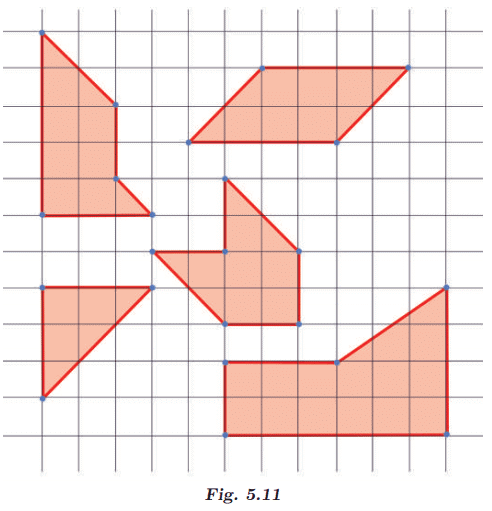
(a) Did you find it challenging to draw some of them?
(b) Which ones?
(c) How did you do it?
Answer

(a) Yes, some line segments are a little more difficult to draw than others.
(b) Line segments e, f, h, and g.
(c) Parallel lines are drawn by keeping them equidistant from the given lines.
23
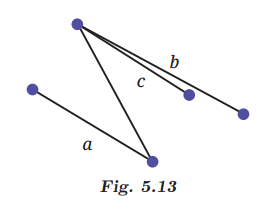
Answer
In the given figure, line a is parallel to line c because these two lines are always the same distance apart and never meet, no matter how far they go.24
In Fig. 5.14, line t intersects lines l and m. t is called a transversal. Notice that 8 angles are formed when a line crosses a pair of lines.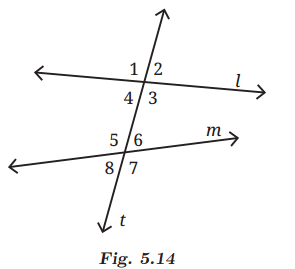
Q: Is it possible for all the eight angles to have different measurements? Why, why not?
Answer
No, all eight angles cannot have different measurements. Vertically opposite angles are equal, so there are at most four distinct angle measures.
25
Answer
Five different angles are not possible, as vertically opposite angles must be equal, limiting the number of distinct angles to four.26

Answer
Tools Needed:
- Ruler
- Set Squares (right-angled triangle)
- Pencil
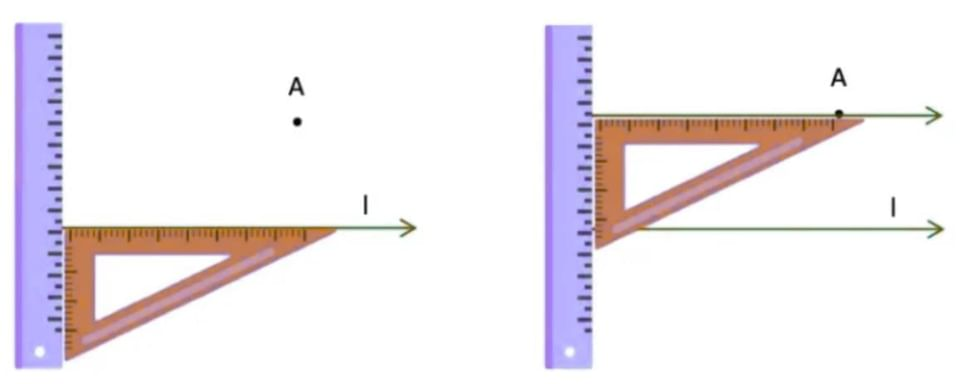
Step-by-Step Procedure:
- Place the set square so that one side is along the line l.
- Hold the ruler against the other side of the set square (the ruler won’t move).
- Slide the set square along the ruler until one side reaches point A.
- Draw a line along the edge of the set square through point A.
- This new line is parallel to line l and passes through point A.
Making Parallel Lines through Paper Folding
Let us try to do the same with paper folding. For a line l (given as a crease), how do we make a line parallel to l such that it passes through point A?
We know how to fold a piece of paper to get a line perpendicular to l. Now, try to fold a perpendicular to l such that it passes through point A. Let us call this new crease t.
Now, fold a line perpendicular to t passing through A again. Let us call this line m. The lines l and m are parallel to each other. 
27
Answer
Line t is perpendicular to line l; line m is also perpendicular to line t. Thus, if two lines are perpendicular to the same line, they are parallel to each other. Thus, lines l and m are parallel to each other because they share the same perpendicular relationship with line t.28
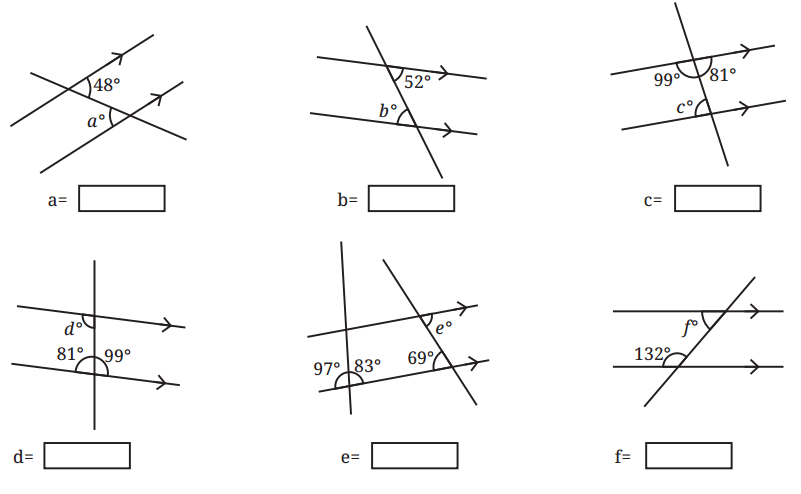
Answer
(a) Since alternate interior angles formed by a transversal intersecting a pair of parallel lines are always equal to each other. Therefore, a = 48°
(b) Since alternate angles formed by a transversal intersecting a pair of parallel lines are always equal to each other. Therefore, b = 52°.
(c) The sum of the interior angles on the same side of the transversal always adds up to 180°. So, 180° – 99° = 81°. Therefore, c = 81°.
(d) The sum of the interior angles on the same side of the transversal always adds up to 180°. So, 180° – 81° = 99°. Therefore, d = 99°
(e) Alternate interior angles formed by a transversal intersecting a pair of parallel lines are always equal to each other. Therefore, e = 69°.
(f) The sum of the interior angles on the same side of the transversal always adds up to 180°. So, 180°- 132° = 48°. Therefore, f = 48°.
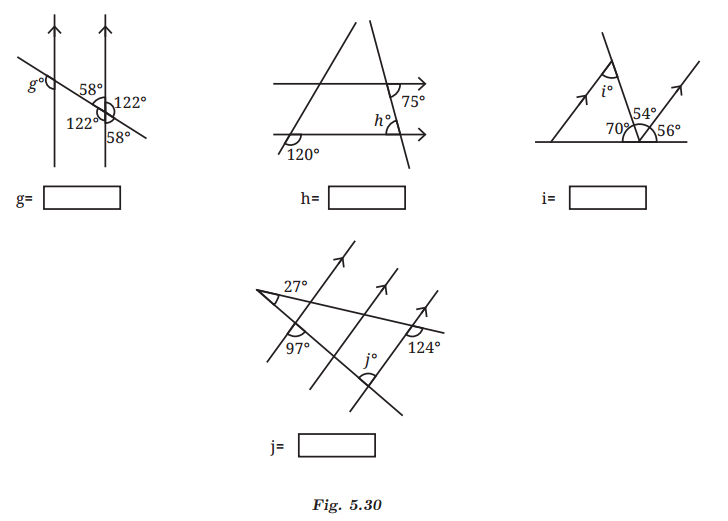
(g) Corresponding angles formed by a transversal intersecting a pair of parallel lines are always equal to each other. Therefore, g = 122°.
(h) Alternate interior angles formed by a transversal intersecting a pair of parallel lines are always equal to each other. Therefore, h = 15°.
(i) Alternate interior angles formed by a transversal intersecting a pair of parallel lines are always equal to each other. Therefore, i = 54°.
(j) Alternate interior angles formed by a transversal intersecting a pair of parallel lines are always equal to each other. Therefore, j = 97°.
29
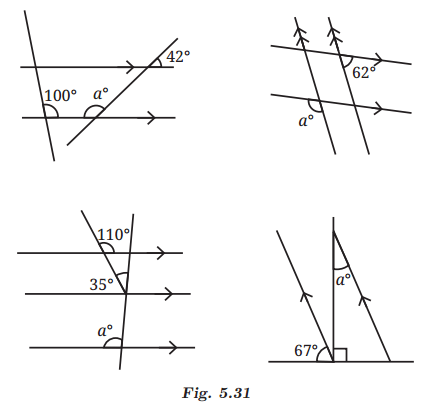
Answer
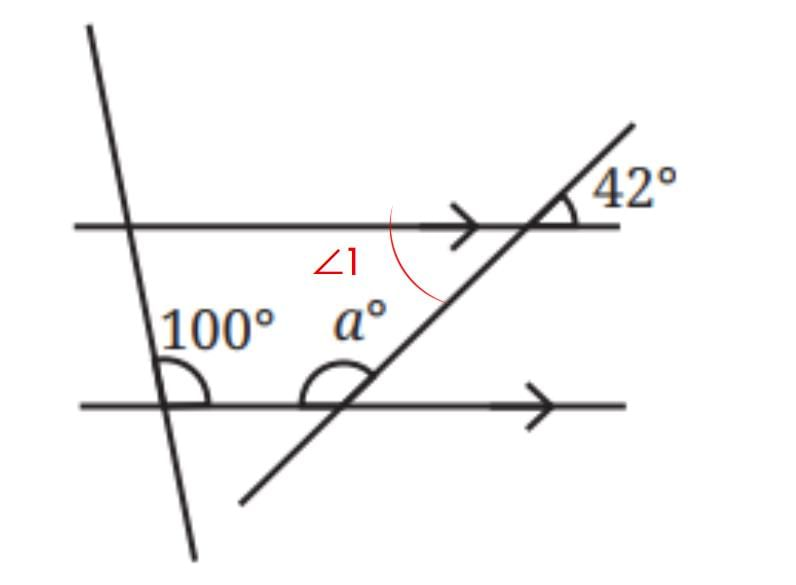
∠1 = 42° ( Vertically opposite angles)
42° + a° = 180° ( Co-interior angles)
⇒ a° = 180° - 42°
⇒ a° = 138°
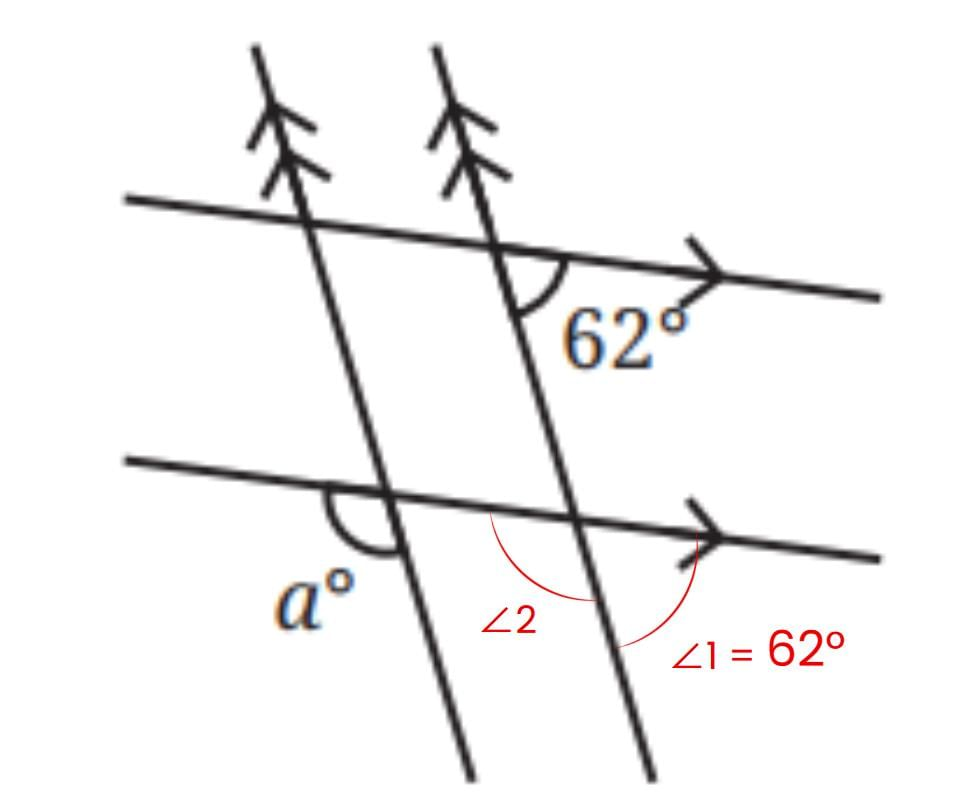
∠1 = 62° (Corresponding angles are equal)
∠1 + ∠2 = 180° ( Linear Pair)
⇒ 62° + ∠2 = 180°
⇒ ∠2 = 118°
Now, a° = 118° (Corresponding angles are equal)
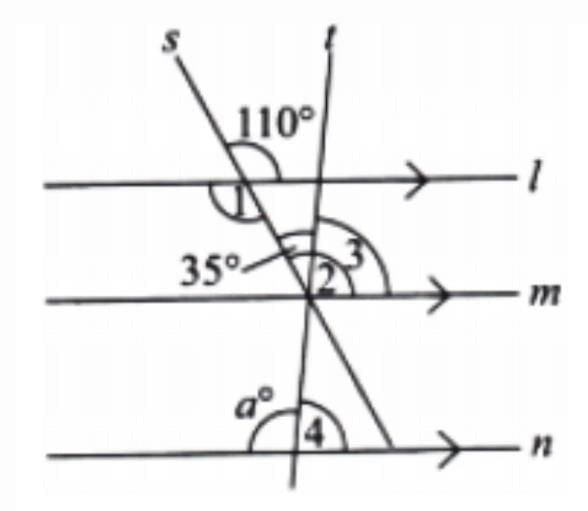
Here, lines s and l are intersecting lines.
So, ∠1 = 110° [Vertically opposite angles]
And ∠1 = ∠2 = 110° because lines l and m are parallel and line s is a transversal.
Therefore ∠3 = ∠2 – 35° = 110° – 35° = 75°
Also, ∠3 = ∠4 = 75° [Corresponding angles]
So, a° = 180° – 75° = 105° [Linear pair angles]
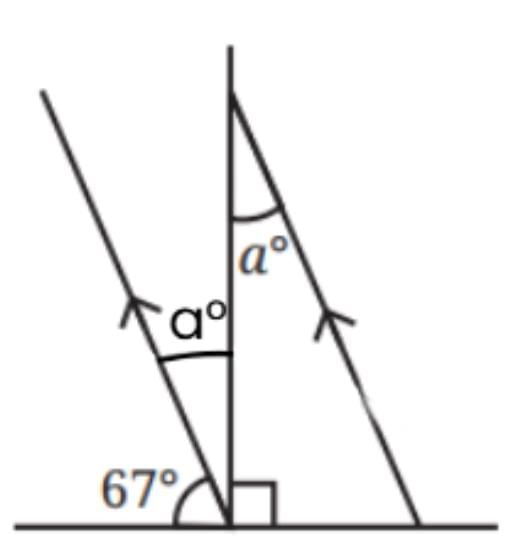
67° + a° + 90° = 180° ( Using angles on a straight line)
⇒ a°= 23° ( Also, alternate angles are equal).
30
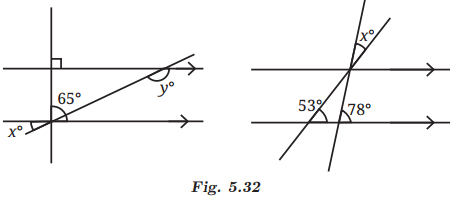
Answer
In Fig. 5.32 (left), there is the correction in the image. 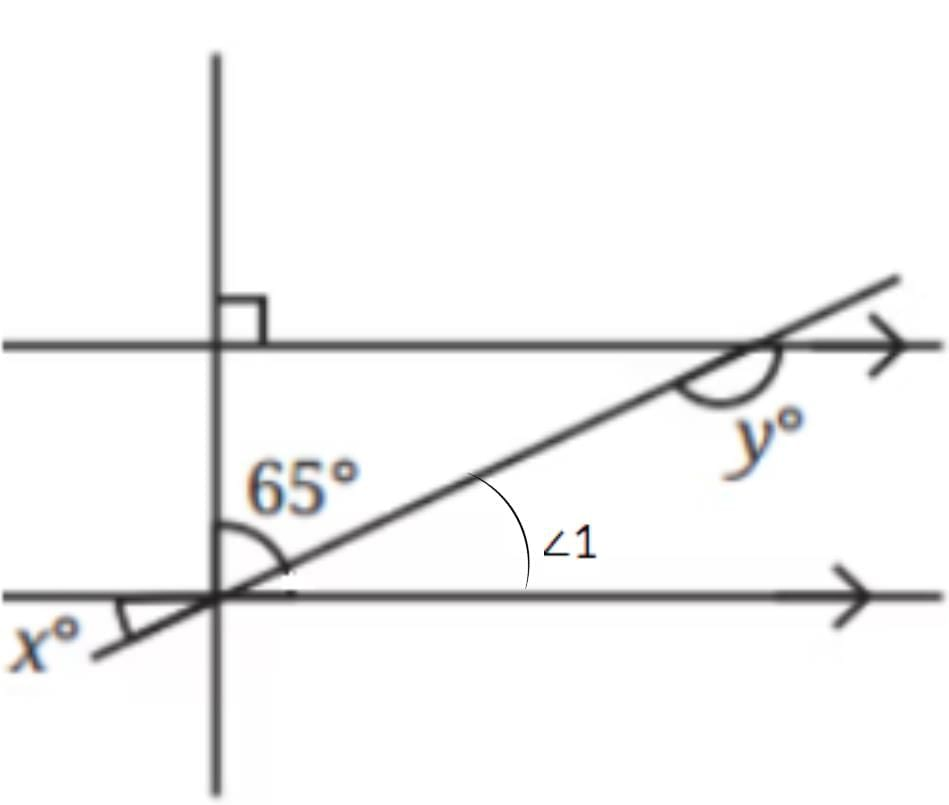
∠1 = x° ( Alternate angles)
∠1 + 65° = 90° ( Linear Pair)
⇒ x + 65° = 90°
⇒ x° = 25°
x° + y = 180° ( Co-interior angles)
⇒ y = 180° - 25° = 155°
In Fig. 5.32 (right), 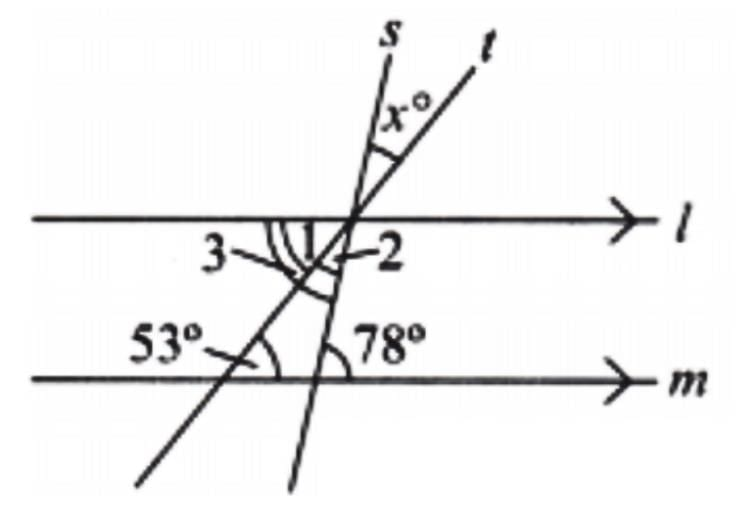
Since lines l and m are parallel and line s is a transversal.
So, ∠3 = 78° [Alternate Angles]
Also, lines l and m are parallel, and line t is a transversal.
So, ∠1 = 53° [Alternate Angles]
Therefore, ∠2 = ∠3 – ∠1 = 78° – 53° = 25°
Lines s and t are intersecting lines.
Therefore, x° = ∠2 = 25° [ Vertically Opposite Angles]
31
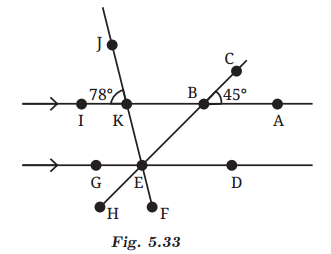
Answer
Line segments IA and HC intersect at point B.So, ∠ABC = ∠KBE = 45° [Vertically Opposite Angles]
Similarly, line segments JF and IA intersect at point K.
So, ∠IKJ = ∠BKE = 78° [Vertically Opposite Angles]
∠KBE = ∠GEH = 45° [Corresponding Angles]
Similarly, ∠BKE = ∠FED = 78° [Corresponding Angles]
Now, ∠GEH + ∠HEF + ∠FED = 180° [Linear Pair]
∠HEF = 180° – 45° – 78° = 57°
32
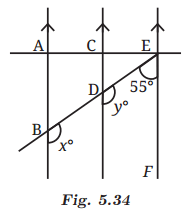
Answer
Given AB is parallel to CD and CD is parallel to EF.So, AB is parallel to EF.
Now, EF is parallel to CD, and DE is a transversal.
So, y° + 55° = 180° [Sum of interior angles]
y = 125°
Now, AB is parallel to CD, and BD is a transversal.
So, x° =y° = 125° [Corresponding Angles]
33
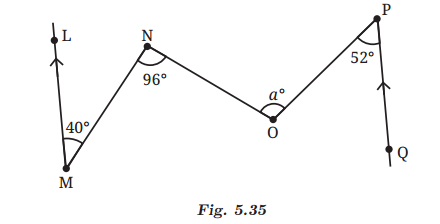
Answer
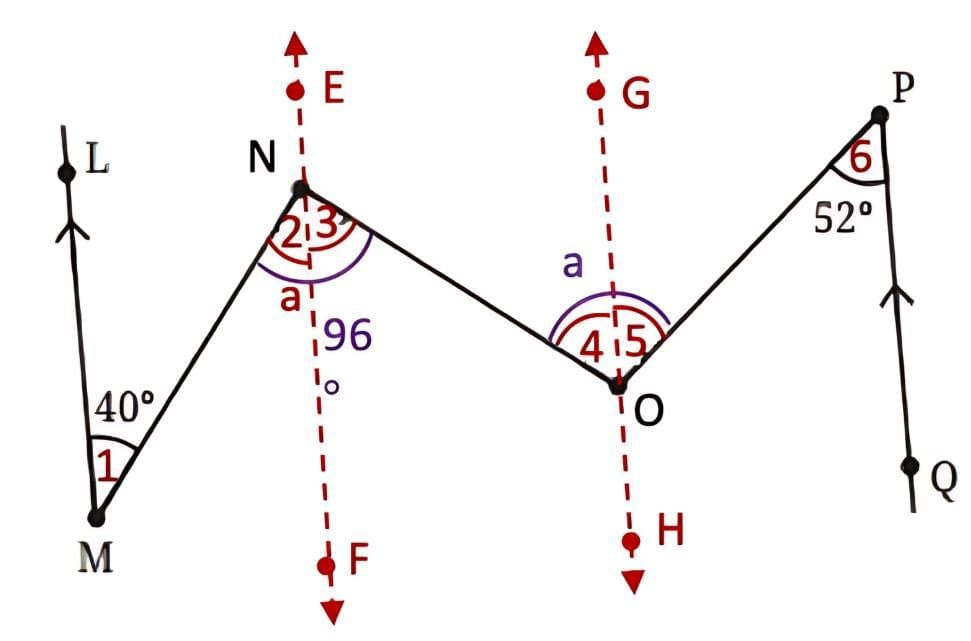
Construction: Draw lines EF and GH parallel to lines LM and PQ.
LM is parallel to EF and MN is a transversal, then
∠1 = ∠2 = 40°…….. (Alternate interior angles)
∠2 + ∠3 = 96°
40° + ∠3 = 96°
∠3 = 96° – 40°
∠3 = 56°.
EF is parallel to GH and NO is a transversal, then
∠3 = ∠4 = 56°…….. (Alternate interior angles)
Also, GH is parallel to PQ and OP is a transversal, then
∠5 = ∠6 = 52°…….. (Alternate interior angles)
a = ∠4 + ∠5
a = 56° + 52°
a = 108°.
34
Q: There do not seem to be any parallel lines here. Or, are there? 
What causes these illusions?
Answer
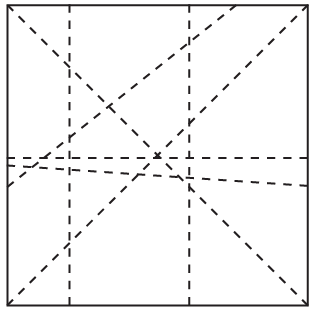
(a) At first glance, this image may appear to be a confusing mix of lines going in all directions, giving the impression that nothing is straight or parallel. However, if we take a closer look, we can see that the vertical lines are perfectly straight, evenly spaced, and are parallel. In contrast, the other lines in the image fan out like spokes on a wheel. These lines are not parallel; they are slanted and converge at a central point. Due to their orientation and the way they intersect with the vertical lines, our brains can become misled. This phenomenon is known as an optical illusion. It occurs because the slanted lines create a sensation that everything is angled or distorted. The focal point in the centre draws our attention and makes it difficult to concentrate on the vertical lines.
(b) This pattern appears to be filled with tilted or zigzagging lines, and the black shapes create a confusing background. However, if we look closely at the white spaces in between, we can see that the horizontal white lines are parallel. So why do they not seem that way? The bold, slanted black shapes visually interrupt the lines, causing our eyes to perceive them as slanting or shifting. This phenomenon is known as an optical illusion—our brain interprets the shapes around the lines, leading us to see something that isn’t there.
(c) When you first look at this picture, it appears that nothing is parallel. The lines seem bent, the shape appears to curve inward, and everything feels like it’s being pulled toward the centre. However, the two horizontal lines at the top and bottom of the image are parallel! This is a classic optical illusion. It occurs because of the many diagonal lines radiating from a central point, resembling the spokes of a wheel. These radiating lines distort our perception, leading our brains to interpret the space as curved due to the way the lines fan out from the centre, creating a sense of depth. As a result, the ends of the horizontal lines seem to bend, even though they are perfectly straight. This visual trick deceives our eyes into believing that the horizontal lines are curving inward, but if we measure them or place a ruler along them, we can see that they are straight and parallel.