NCERT Solutions for Chapter 11 Constructions Class 10 Maths
Book Solutions1
Draw a line segment of length 7.6 cm and divide it in the ratio 5 : 8.
Measure the two parts.
Measure the two parts.
Answer
Steps of construction:
I. Draw a line segment AB = 7.6 cm.
II. Draw a ray AX making an acute angle with AB.
III. Mark 13 (8 + 5) equal points on AX, and mark them as X1, X2, X3, ........, X13.
IV. Join ‘point X13’ and B.
V. From ‘point X5’, draw X5C ║ X13B, which meets AB at C.
Thus, C divides AB in the ratio 5 : 8.
On measuring the two parts, we get: AC = 4.7 cm and BC = 2.9 cm.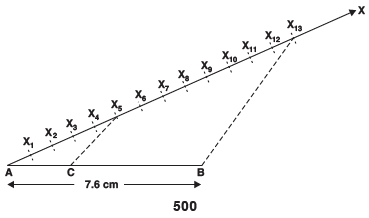
Justification:
In Δ ABX13 and Δ ACX5, we have
Exercise 11.1
Page Number 219
2
Construct a triangle of sides 4 cm, 5 cm and 6 cm and then a triangle similar to it whose sides are 2/3 of the corresponding sides of the first triangle.
Answer
Steps of construction:I. Draw a ∆ ABC such that BC = 6 cm, AC = 5 cm and AB = 4 cm.
II. Draw a ray BX making an acute angle ∠CBX.
III. Mark three points X1, X2, X3 on BX such that BX1 = X1X2 = X2X3.
IV. Join X3C.
V. Draw a line through X2 such that it is parallel to X3C and meets BC at C′.
VI. Draw a line through C′ parallel to CA to intersect BA at A′.
Thus, A′BC′ is the required triangle.

Exercise 11.1
Page Number 220
3
Construct a triangle with sides 5 cm, 6 cm and 7 cm and then another triangle whose sides are 7/5 of the corresponding sides of the first triangle.
Answer
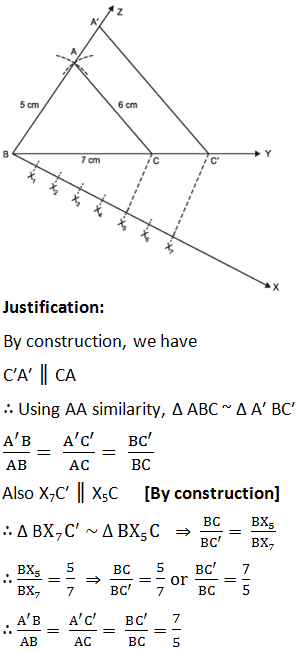
Steps of construction:I. Construct a Δ ABC such that AB = 5 cm, BC = 7 cm and AC = 6 cm.
II. Draw a ray BX such that ∠CBX is an acute angle.
III. Mark 7 points of X1, X2, X3, X4, X5, X6 and X7 on BX such that BX1 = X1X2 = X2X3= X3X4 = X4X5 = X5X6 = X6X7
IV. Join X5 to C.
V. Draw a line through X7 intersecting BC (produced) at C′ such that X5 C ║ X7 C′.
VI. Draw a line through C′ parallel to CA to intersect BA (produced) at A′. Thus, Δ A′BC′ is the required triangle.
Exercise 11.1
Page Number 220
4
Construct an isosceles triangle whose base is 8 cm and altitude 4 cm and then another triangle whose sides are 1 times the corresponding sides of the isosceles triangle.
Answer
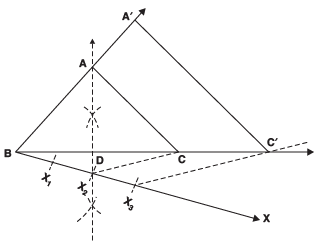
Steps of construction:I. Draw BC = 8 cm
II. Draw the perpendicular bisector of BC which intersects BC at D.
III. Mark a point A on the above perpendicular such that DA = 4 cm.
IV. Join AB and AC.
Thus, Δ ABC is the required isosceles triangle.
V. Now, draw a ray BX such that ∠CBX is an acute angle.
VI. On BX, mark three points X1, X2 and X3 such that: BX1 = X1X2 = X2X3
VII. Join X2 to C.
VIII. Draw a line through X3 parallel to X2 C and intersecting BC (extended) to C′ .
IX. Draw a line through C′ parallel to CA intersecting BA (extended) at A′, thus, Δ A′BC′ is the required triangle.

Exercise 11.1
Page Number 220
5
Draw a triangle ABC with side BC = 6 cm, AB = 5 cm and ∠ ABC = 60°. Then construct a triangle whose sides are 3/4 of the corresponding sides of the triangle ABC.
Answer
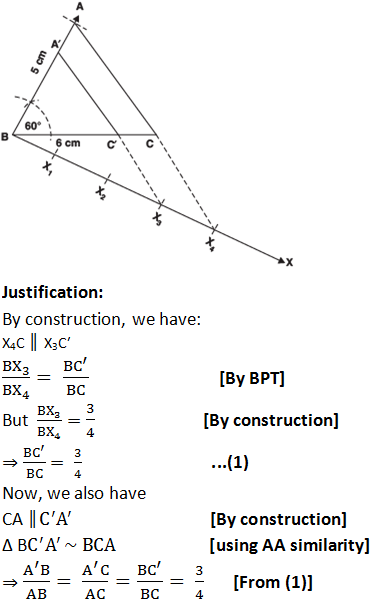
Steps of construction:I. Construct a ΔABC such that BC = 6 cm, AB = 5 cm and ∠ABC = 60°.
II. Draw a ray such that ∠CBX is an acute angle.
III. Mark four points X1, X2, X3 and X4 on BX such that BX1 = X1X2 = X2X3 = X3X4
IV. Join X4C and draw X3C′ ║ X4C such that C′ is on BC.
V. Also draw another line through C′ and parallel to CA to intersect BA at A′.
Thus, ΔA′BC′ is the required triangle.
Exercise 11.1
Page Number 220
6
Draw a triangle ABC with side BC = 7 cm, ∠ B = 45°, ∠ A = 105°. Then, construct a triangle whose sides are 4/3 times the corresponding sides of Δ ABC.
Answer
Steps of construction:I. Construct a Δ ABC such that BC = 7 cm, ∠B = 45° and ∠A = 105°.
II. Draw a ray BX making an acute angle ∠CBX with BC.
III. On BX, mark four points X1, X2, X3 and X4 such that BX1 = X1X2 = X2X3 = X3X4.
IV. Join X3 to C.
V. Draw X4C′ ║ X3C such that C′ lies on BC (extended).
VI. Draw a line through C′ parallel to CA intersecting the extended line segment BA at A′.


Exercise 11.1
Page Number 220
7
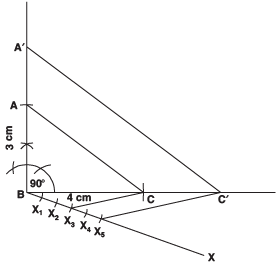
Draw a right triangle in which the sides (other than hypotenuse) are of lengths 4 cm and 3 cm. Then construct another triangle whose sides are 5/3 times the corresponding sides of the given triangle.
Answer
Steps of construction:I. Construct the right triangle ABC such that ∠B = 90°, BC = 4 cm and BA = 3 cm.
II. Draw a ray BX such that an acute angle ∠CBX is formed.
III. Mark 5 points X1, X2, X3, X4 and X5 on BX such that BX1 = X1X2 = X2X3 = X3X4 = X4X5.
IV. Join X3 to C.
V. Draw a line through X5 parallel to X3C, intersecting the extended line segment BC at C′.
VI. Draw another line through C ′ parallel to CA intersecting the extended line segment BA at A′.
Thus, Δ A′ BC′ is the required triangle.

Exercise 11.1
Page Number 220
1
In each of the following, give also the justification of the construction:
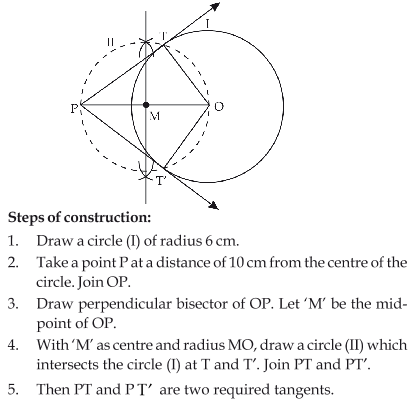
Draw a circle of radius 6 cm. From a point 10 cm away from its centre, construct the pair of tangents to the circle and measure their lengths.
Answer

Exercise 11.2
Page Number 221
2
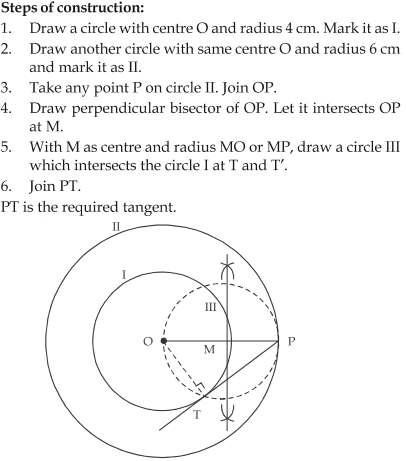
Construct a tangent to a circle of radius 4 cm from a point on the concentric circle of radius 6 cm and measure its length. Also verify the measurement by actual calculation.
Answer


Exercise 11.2
Page Number 221
3
Draw a circle of radius 3 cm. Take two points P and Q on one of its extended diameters each at a distance of 7 cm from its centre. Draw tangents to the circle from these two points P and Q.
Answer


Exercise 11.2
Page Number 221
4
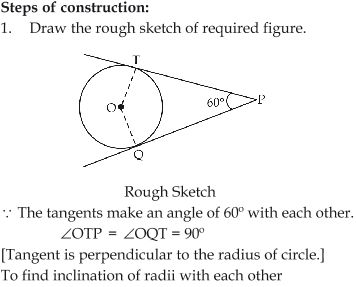
Draw a pair of tangents to a circle of radius 5 cm which are inclined to each other at an angle of 60°.
Answer

Exercise 11.2
Page Number 221
5
Draw a line segment AB of length 8 cm. Taking A as centre, draw a circle of radius 4 cm and taking B as centre, draw another circle of radius 3 cm. Construct tangents to each circle from the centre of the other circle.
Answer
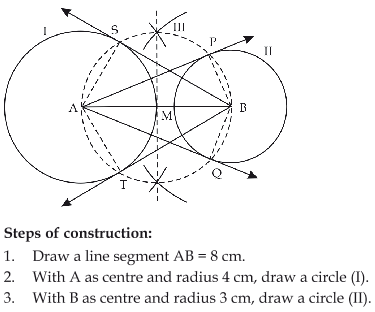

Exercise 11.2
Page Number 221
6
Let ABC be a right triangle in which AB = 6 cm, BC = 8 cm and ∠ B = 90°. BD is the perpendicular from B on AC. The circle through B, C, D is drawn. Construct the tangents from A to this circle.
Answer
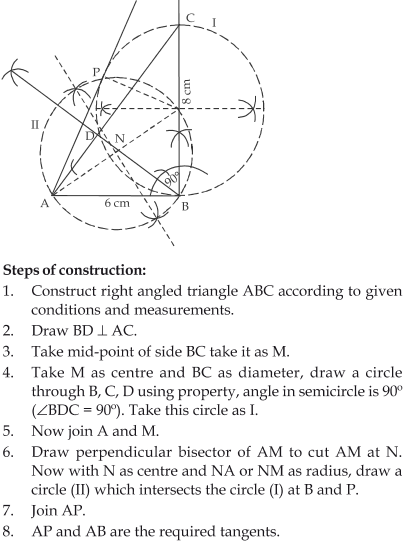

Exercise 11.2
Page Number 222
7
Draw a circle with the help of a bangle. Take a point outside the circle. Construct the pair of tangents from this point to the circle
Answer
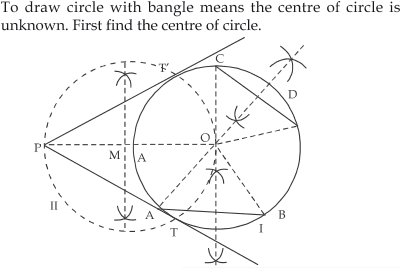


Exercise 11.2
Page Number 222