NCERT Solutions for Chapter 10 Circles Class 9 Maths
Book Solutions1
Fill in the blanks:
(i) The centre of a circle lies in _________ of the circle.
(ii) A point, whose distance from the centre of a circle is greater than its radius lies in _________ of the circle.
(iii) The longest chord of a circle is a _________ of the circle.
(iv) An arc is a _________ when its ends are the ends of a diameter.
(v) Segment of a circle is the region between an arc and _________ of the circle.
(vi) A circle divides the plane, on which it lies, in _________ parts.
(i) The centre of a circle lies in _________ of the circle.
(ii) A point, whose distance from the centre of a circle is greater than its radius lies in _________ of the circle.
(iii) The longest chord of a circle is a _________ of the circle.
(iv) An arc is a _________ when its ends are the ends of a diameter.
(v) Segment of a circle is the region between an arc and _________ of the circle.
(vi) A circle divides the plane, on which it lies, in _________ parts.
Answer
(i) interior(ii) exterior
(iii) diameter
(iv) semicircle
(v) the chord
(vi) three
Exercise 10.1
Page Number 171
2
Write True or False. Give reasons for your answers.
(i) Line segment joining the centre to any point on the circle is a radius of the circle.
(ii) A circle has only finite number of equal chords.
(iii) If a circle is divided into three equal arcs, each is a major arc.
(iv) A chord of a circle, which is twice as long as its radius, is a diameter of the circle.(v) Sector is the region between the chord and its corresponding arc.
(vi) A circle is a plane figure.
(i) Line segment joining the centre to any point on the circle is a radius of the circle.
(ii) A circle has only finite number of equal chords.
(iii) If a circle is divided into three equal arcs, each is a major arc.
(iv) A chord of a circle, which is twice as long as its radius, is a diameter of the circle.(v) Sector is the region between the chord and its corresponding arc.
(vi) A circle is a plane figure.
Answer
(i) True [∵ All points on the circle are equidistant from the centre](ii) False [∵ A circle can have an infinite number of equal chords.]
(iii) False [∵ Each part will be less than a semicircle.]
(iv) True [∵ Diameter = 2 × Radius]
(v) False [∵ The region between the chord and its corresponding arc is a segment.]
(vi) True [∵ A circle is drawn on a plane.]
Exercise 10.1
Page Number 171
1
Recall that two circles are congruent if they have the same radii. Prove that equal chords of congruent circles subtend equal angles at their centres.
Answer
We have a circle having its centre at O and two equal chords AB and CD such that they subtend ∠AOB and ∠COD respectively at the centre, i.e. at O.We have to prove that ∠AOB = ∠COD
Now, in ΔAOB and ΔCOD, we have
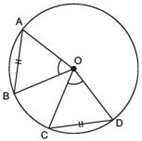
AO = CO [Radii of the same circle]
BO = DO [Radii of the same circle]
AB = CD [Given]
∴ ΔAOB ≌ ΔCOD [SSS criterion]
⇒ Their corresponding parts are equal.
∴ ∠AOB = ∠COD
Exercise 10.2
Page Number 173
2
Prove that if chords of congruent circles subtend equal angles at their centres, then the chords are equal.
Answer
We have a circle having its centre at O, and its two chords AB and CD such that∠AOB = ∠COD
We have to prove that AB = CD
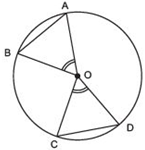
∵ In ΔAOB and ΔCOD, we have:
AO = CO [Radii of the same circle]
BO = DO [Radii of the same circle]
∠AOB = ∠COD [Given]
∴ ΔAOB ≌ ΔCOD [SAS criterion]
∴ Their corresponding parts are equal, i.e. AB = CD
Exercise 10.2
Page Number 173
1
Draw different pairs of circles. How many points does each pair have in common? What is the maximum number of common points?
Answer
Let us draw different pairs of circles as shown below: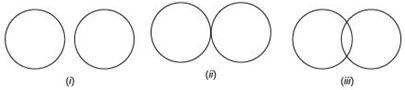
We have
| In figure | Maximum number of common points |
| (i) | nil |
| (ii) | one |
| (iii) | two |
Thus, two circles can have at the most two points in common.
Exercise 10.3
Page Number 176
2
Suppose you are given a circle. Give a construction to find its centre.
Answer
Steps of construction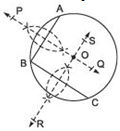
I . Take any three points on the given circle. Let these be A, B and C.
II. Join AB and BC.
III . Draw the perpendicular bisector PQ of AB.
IV. Draw the perpendicular bisector RS of BC such that it intersects PQ at O.
Thus, ‘O’ is the required centre of the given circle.
Exercise 10.3
Page Number 176
3
If two circles intersect at two points, prove that their centres lie on the perpendicular bisector of the common chord.
Answer
We have two circles with centres O and O', intersect at A and B.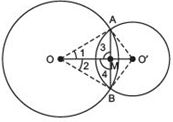
∵ AB is the common chord of two circles and OO' is the line segment joining the centres of the circles. Let OO' and AB intersect each other at M.
∴ To prove that OO' is the perpendicular bisector AB, we join OA, OB, O'A and O'B.
Now, in ΔOAO' and ΔOBO',
we have, OA = OB [Radii of the same circle]
O'A= O'B [Radii of the same circle]
OO' = OO' [Common]
∴ Using the SSS criterion,
ΔOAO'≌ ΔOBO'
⇒ ∠1= ∠2 [c.p.c.t.]
Now, in ΔAOM and ΔBOM,
OA = OB [Radii of the same circle]
OM = OM [Common]
∠1= ∠2 [Proved]
∴ ΔOAM ≌ ΔBOM [SAS criterion]
⇒ ∠3= ∠4 [c.p.c.t.]
But ∠3 + ∠4 = 180º [Linear pair]
∴ ∠3= ∠4 = 90º each.
⇒ AM ⊥ OO'
Also, AM = BM [c.p.c.t.]
⇒ M is the mid-point of AB.
Thus, OO' is the perpendicular bisector of AB.
Exercise 10.3
Page Number 176
1
Two circles of radii 5 cm and 3 cm intersect at two points and the distance between their centres is 4 cm. Find the length of the common chord.
Answer
We have two intersecting circles with centres at O and O' respectively.
Let PQ be the common chord.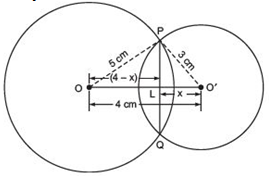
∵ In two intersecting circles, the line joining their centres is perpendicular bisector of the common chord.
∴ ∠OLP = ∠OLP = 90º
PL = PQ
Now in right ΔOLP,
PL2 + OL2 = OP2
⇒ PL2 + (4 - x)2 = 52
⇒ PL2 = 52 - (4 - x)2
⇒ PL2 = 25 - 16 - x2 + 8x
⇒ PL2 = 9 - x2 + 8x ...(1)
Again, in ΔO'LP,
PL2 = 32 - x2 = 9 - x2 ...(2)
From (1) and (2),
we have,
9 - x2 + 8x = 9 - x2
⇒ 8x = 0
⇒ x= 0
⇒ L and O' coincide.
∴ PQ is a diameter of the smaller circle.
⇒ PL = 3 cm
But, PL = LQ
∴ LQ = 3 cm
∴ PQ = PL + LQ
= 3 cm + 3 cm = 6 cm
Thus, the required length of the common chord = 6 cm.
Exercise 10.4
Page Number 179
2
If two equal chords of a circle intersect within the circle, prove that the segments of one chord are equal to corresponding segments of the other chord.
Answer
We have a circle with centre O. Equal chords AB and CD intersect at E.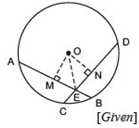
To prove that, AE = DE and CE = BE,
draw OM ⊥ AB and ON ⊥ CD.
Since AB = CD [Given]
∴ OM = ON [Equal chords are equidistant from the centre]
Now, in right ΔOME and right ΔONE,
OM = ON [Proved]
OE = OE [Common]
∴ ΔOME ≌ ΔONE [RHS criterion]
⇒ ME = NE [c.p.c.t.]
⇒ (1/2) AE = (1/2) DE [Perpendiculars from the centre bisect the chord.]
⇒ AE = DE ...(1)
Since, AB = CD (Given)
∴ AB - AE = CD - DE
⇒ CE = BE ...(2)
From (1) and (2),
We have, AE = DE and CE = BE
Exercise 10.4
Page Number 179
3
If two equal chords of a circle intersect within the circle, prove that the line joining the point of intersection to the centre makes equal angles with the chords.
Answer
We have a circle with centre O and equal chords AB and CD are intersecting at E. OE is joined.To prove that ∠1 = ∠2, let us draw OM ⊥ AB and ON ⊥ CD.
In right ΔOME and right ΔONE,
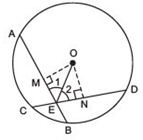
OM = ON [Equal chords are equidistant from the centre.]
OE = OE [Common]
∴ ΔOME ≌ΔONE [RHS criterion]
⇒ Their corresponding parts are equal.
∴ ∠OEM = ∠OEN
or ∠OEA = ∠OED
Exercise 10.4
Page Number 179
4
If a line intersects two concentric circles (circles with the same centre) with centre O at A, B, C and D, prove that AB = CD (see figure).
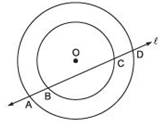
Answer
We have two circles with the common centre O.
A line ‘l’ intersects the outer circle at A and D and the inner circle at B and C. To prove that AB = CD, let us draw OM ⊥ ℓ.
For the outer circle,
∵ OM ⊥ ℓ [Construction]
∴ AM = M D [∵ Perpendicular from the centre bisects the chord] ...(1)
For the inner circle,
∵ OM ⊥ ℓ [Construction]
∴ BM = MC [Perpendicular from the centre to the chord bisects the chord] ...(2)
Subtracting (2) from (1), we have,
AM - BM = MD - MC
⇒ AB = CD
Exercise 10.4
Page Number 179
5
Three girls Reshma, Salma and Mandip are playing a game by standing on a circle of radius 5 m drawn in a park. Reshma throws a ball to Salma, Salma to Mandip, Mandip to Reshma. If the distance between Reshma and Salma and between Salma and Mandip is 6 m each, what is the distance between Reshma and Mandip?
Answer
Let the three girls Reshma, Salma and Mandip are positioned at R, S and M, respectively on the circle of radius 5 m.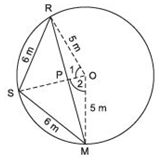
∵ RS = SM = 6 m [Given]
∵ Equal chords of a circle subtend equal angles at the centre.
∴ ∠1 = ∠2
In ΔPOR and ΔPOM,
OP = OP [Common]
OR = OM [Radii of the same circle]
∠1= ∠2 [Proved]
∴ ΔPOR ≌ ΔPOM [SAS criterion]
⇒ Their corresponding parts are equal.
∴ PR = PM and ∠OPR = ∠OPM
∵ ∠OPR + ∠OPM = 180º [Linear pairs]
∴ ∠OPR = ∠OPM = 90º
⇒ OP ⊥ RM
Now, in ΔRSP and ΔMSP,
RS = MS (6 m each)
SP = SP (Common)
∠RSP = ∠MSP
∴ ΔRSP ≌ ΔMSP [SAS criterion]
⇒ RP = MP and ∠RPS = ∠MPS [c.p.c.t]
But, ∠RPS + ∠MPS = 180°
⇒ ∠RPS = ∠MPS = 90º (Each)
∴ SP passes through O.
Let OP = x m
∴ SP = (5 - x) m
Now, in right ΔOPR,
x2 + RP2 = 52 …(1)
In right ΔSPR,
(5 - x)2 + RP2 = 62 …(2)
From (1),
RP2 = 52 - x2
From (2),
RP2 = 62 - (5 - x)2
∴ 52 - x2 = 62 - (5 - x)2
⇒ 25 - x2 = 36 - [25 - 10x + x2]
⇒ 25 - x2 - 36 + 25 - 10x + x2 = 0
⇒ -10x + 14 = 0
⇒ 10x = 14
⇒ x= (14/10) = 1.4
Now,
RP2 = 52 - x2
⇒ RP2 = 25 - (1.4)2
⇒ RP2 = 25 - 1.96 = 23.04 m
∴ RP =√(23.04) = 4.8 m
∴ RM = 2 RP = 2 x 4.8 m = 9.6 m
Thus, distance between Reshma and Mandip is 9.6 m.
Exercise 10.4
Page Number 179
6
A circular park of radius 20 m is situated in a colony. Three boys Ankur, Syed and David are sitting at equal distance on its boundary each having a toy telephone in his hands to talk each other. Find the length of the string of each phone.
Answer
In the figure, let Ankur, Syed and David are sitting at A, S and D respectively such that AS = SD = AD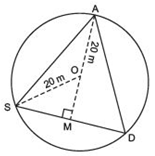
i.e. ΔASD is an equilateral triangle.
Let the length of each side of the equilateral triangle is 2x metres.
Let us draw AM⊥SD.
Since ΔASD is an equilateral,
∴ AM passes through O.
⇒ SM = (1/2)SD = (1/2)(2x)
⇒ SM = x
Now, in right ΔASM,
AM2 + SM2 = AS2
⇒ AM2 = AS2 - SM2
⇒ AM2 = (2x)2 -x2
⇒ AM2 = 4x2 - x2
⇒ AM2 = 3x2
⇒ AM = 3x
Now,
OM = AM - OA = ( 3x - 20) m
Again, in right ΔOBM, we have
OS2 = SM2 + OM2
⇒ 202 = x2 + (3x - 20)2
⇒ 400 = x2 + 3x2 - 403 x + 400
⇒ 4x2 - 403 x= 0
⇒ 4x (x - 103) = 0
⇒ x = 0 or x = 103
But x = 0 is not required.
∴ x= 103 m
Now, SD = 2×m = 2 × 103 m
Thus, the length of the string of each phone = 2 × 103 m.
Exercise 10.4
Page Number 179
1
In the figure, A, B and C are three points on a circle with centre O such that ∠ BOC = 30º and ∠AOB = 60°. If D is a point on the circle other than the arc ABC, find ∠ADC.
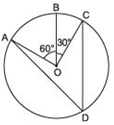
Answer
We have a circle with centre O, such that∠ AOB = 60º and ∠BOC = 30º
∵ ∠AOB + ∠BOC = ∠AOC
∴ ∠AOC = 60º + 30º = 90º
Now, the arc ABC subtends ∠AOC = 90º at the centre and ∠ADC at a point D on the circle other than the arc ABC.
Exercise 10.5
Page Number 184
2
A chord of a circle is equal to the radius of the circle. Find the angle subtended by the chord at a point on the minor arc and also at a point on the major arc.
Answer
We have a circle having a chord AB equal to radius of the circle.∴ AO = BO = AB
⇒ ΔAOB is an equilateral triangle.
Since, each angle of an equilateral = 60º.
⇒ ∠AOB = 60º
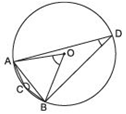
Since the arc ACB makes reflex,
∠AOB = 360º - 60º = 300º at the centre of the circle and ∠ABC at a point on the minor arc of the circle.
Thus,
the angle subtended by the chord on the minor arc = 150º and
on the major arc = 30º.
Exercise 10.5
Page Number 185
3
In the figure, ∠ PQR = 100º, where P, Q and R are points on a circle with centre O. Find ∠OPR.
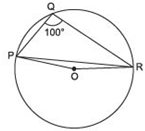
Answer
∵ The angle subtended by an arc of a circle at its centre is twice the angle subtended by the same arc at a point on the circumference.∴ reflex ∠POR = 2∠PQR
But, ∠PQR = 100º
∴ reflex ∠POR = 2 × 100º = 200º
Since,
∠POR + reflex ∠POR = 360º
∴ ∠POR + 200º = 360º
⇒ ∠POR = 360º - 200º
⇒ ∠POR = 160º
Since, OP = OR [Radii of the same circle]
∴ In ΔPOR,
∠OPR = ∠ORP [Angles opposite to equal sides of a triangle are equal]
Also,
∠OPR + ∠ORP + ∠POR = 180º [Sum of the angles of a triangle = 180°]
⇒ ∠OPR + ∠OPR + 160º = 180º [∵ ∠OPR = ∠ORP]
⇒ 2∠OPR = 180º ∠ 160º = 20º
⇒ ∠OPR = (20º/2)= 10º
Exercise 10.5
Page Number 185
4
In the figure, ∠ABC = 69º, ∠ACB = 31º, find ∠BDC.
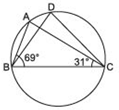
Answer
We have, in ΔABC,∠ABC = 69º and ∠ACB = 31º
But ∠ABC + ∠ACB + ∠BAC = 180º
∴ 69º + 31º + ∠BAC = 180º
⇒ ∠BAC = 180º - 69º - 31º = 80º
Since, angles in the same segment are equal.
∴ ∠BDC = ∠BAC
⇒ ∠BDC = 80º
Exercise 10.5
Page Number 185
5
In the figure, A, B, C and D are four points on a circle. AC and BD intersect at a point E such that ∠BEC = 130° and ∠ECD = 20º.
Find ∠BAC.
Find ∠BAC.
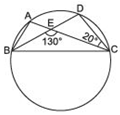
Answer
In ΔCDE,Exterior ∠BEC = {Sum of interior opposite angles}
[∵ BD is a straight line.]
130º = ∠EDC + ∠ECD
⇒ 130º = ∠EDC + 20º
⇒ ∠EDC = 130º - 20º = 110º
⇒ ∠BDC = 110º
Since, angles in the same segment are equal.
∴ ∠BAC = ∠BDC
⇒ ∠BAC = 110º
Exercise 10.5
Page Number 185
6
ABCD is a cyclic quadrilateral whose diagonals intersect at a point E. If ∠DBC = 70º, ∠BAC is 30º, find ∠BCD. Further, if AB = BC, find ∠ECD.
Answer
∵ Angles in the same segment of a circle are equal.∴ ∠BAC = ∠BDC
⇒ 30º = ∠BDC Also ∠DBC = 70º [Given]
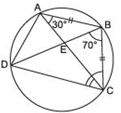
∴ In ΔBCD, we have
∠BCD + ∠DBC + ∠CDB = 180º
[∵ Sum of angles of a triangle is 180º]
⇒ ∠BCD + 70º + 30º = 180º
⇒ ∠BCD = 180º - 70º - 30º = 80º
Now, in ΔABC,
∵ AB = BC [Given]
∴ ∠BCA = ∠BAC [Angles opposite to equal sides of a triangle are equal]
⇒ ∠BCA = 30º [∵ ∠BAC = 30º]
Now,
∠BCA + ∠ECD = ∠BCD
⇒ 30º + ∠ECD = 80º
⇒ ∠ECD = 80º - 30º = 50º
Exercise 10.5
Page Number 185
7
If diagonals of a cyclic quadrilateral are diameters of the circle through the vertices of the quadrilateral, prove that it is a rectangle.
Answer
∵ AC and BD are diameters.∴ AC = BD [∵ All diameters of a circle are equal] …(1)
Since a diameter divides a circle into equal parts.
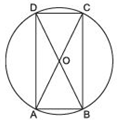
∴ ∠BAD = 90º [∵ Angle formed in a semicircle is 90º]
Similarly,
∠ABC = 90º, ∠BCD = 90º and ∠CDA = 90º
Now, in right ΔABC and right ΔBAD,
AC = BD [From (1)]
AB = AB [Common]
∴ ΔABC ≌ ΔBAD [RHS criterion]
⇒ BC = AD [c.p.c.t.]
Similarly, AB = CD
Thus, the cyclic quadrilateral ABCD is such that its opposite sides are equal and each of its angle is right angle.
∴ ABCD is a rectangle.
Exercise 10.5
Page Number 185
8
If the non-parallel sides of a trapezium are equal, prove that it is cyclic.
Answer
We have a trapezium ABCD such that AB || CD and AD = BC.Let us draw BE || AD such that ABED is a parallelogram.
∵ The opposite angles of a parallelogram are equal.
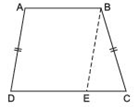
∴ ∠BAD = ∠BED …(1)
and AD = BE [Opposite sides of a parallelogram] …(2)
But AD = BC [Given] …(3)
∴ From (2) and (3), we have,
BE = BC
⇒ ∠BEC = ∠BCE [Angles opposite to equal sides of a triangle D are equal] …(4)
Now,
∠BED + ∠BEC = 180º [Linear pairs]
⇒ ∠BAD + ∠BCE = 180º [Using (1) and (4)]
i.e. A pair of opposite angles of quadrilateral ABCD is 180º.
∴ ABCD is cyclic.
⇒ The trapezium ABCD is a cyclic.
Exercise 10.5
Page Number 185
9
Two circles intersect at two points B and C. Through B, two line segments ABD and PBQ are drawn to intersect the circles at A, D and P, Q respectively (see the figure). Prove that ∠ACP = ∠QCD.
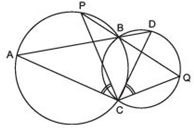
Answer
Since angles in the same segment of a circle are equal.∴ ∠ACP = ∠ABP …(1)
Similarly,
∠QCD = ∠QBD …(2)
Since, ∠ABP = ∠QBD [Vertically opposite angles are equal]
∴ From (1) and (2), we have ∠ACP = ∠QCD
Exercise 10.5
Page Number 186
10
If circles are drawn taking two sides of a triangle as diameters, prove that the point of intersection of these circles lie on the third side.
Answer
We have a DABC, and two circles described with diameters as AB and AC respectively. They intersect in a point D.Let us join A and D.
∵ AB is a diameter.
∴ ∠ADB is an angle formed in a semicircle.
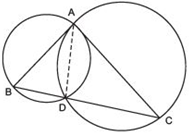
⇒ ∠ADB = 90º …(1)
Similarly, ∠ADC = 90º …(2)
Adding (1) and (2), we have
∠ADB + ∠ADC = 90º + 90º = 180º
i.e. B, D and C are collinear points.
⇒ BC is a straight line.
Thus, D lies on BC.
Exercise 10.5
Page Number 186
11
ABC and ADC are two right triangles with common hypotenuse AC. Prove that ∠CAD= ∠CBD.
Answer
We have right ΔABC and right ΔADC such that they are having AC as their common hypotenuse.∵ AC is a hypotenuse.
∵ ∠ADC = 90º = ∠ABC
∴ Both the triangles are in the same semicircle.
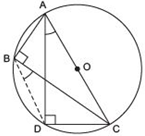
⇒ A, B, C and D are concyclic.
Let us join B and D.
∵ DC is a chord.
∴ ∠CAD and ∠CBD are formed in the same segment.
⇒ ∠CAD = ∠CBD.
Exercise 10.5
Page Number 186
12
Prove that a cyclic parallelogram is a rectangle.
Answer
We have a cyclic parallelogram ABCD.Since, ABCD is a cyclic quadrilateral.
∴ Sum of its opposite angles = 180º
⇒ ∠A + ∠C = 180º …(1)
But ∠A = ∠C …(2)
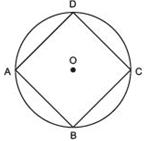
[∵ Opposite angles of parallelogram are equal]
From (1) and (2), we have
∠A= ∠C = 90º
Similarly, ∠B= ∠D = 90º
⇒ Each angle of the parallelogram ABCD is of 90º.
Thus, ABCD is a rectangle.
Exercise 10.5
Page Number 186
1
Prove that the line of centres of two intersecting circles subtends equal angles at the two points of intersection.
Answer
We have two circles with centres O and O' respectively such that they intersect each other at P and Q.To prove that ∠OPO' = ∠OQO',
let us join OP, O'P, OQ, O'Q and OO'.
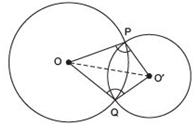
In ΔOPO' and ΔOQO', we have
OP = OQ [Radii of the same circle]
O'P= O'Q [Radii of the same circle]
OO' = OO' [Common]
∴ Using the SSS criterion, ΔOPO'≌ ΔOQO'
∴ Their corresponding parts are equal.
Thus, ∠OPO' = ∠OQO'
Exercise 10.6
Page Number 186
2
Two chords AB and CD of lengths 5 cm and 11 cm respectively of a circle are parallel to each other and are on opposite sides of its centre. If the distance between AB and CD is 6 cm, find the radius of the circle.
Answer
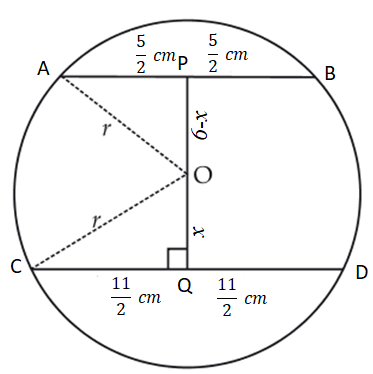
Let ‘r’ be the radius of the circle.
Let us draw OP ⊥ AB and OQ ⊥ CD.
We join OA and OC.
Let OQ = x cm
∴ OP = (6 - x) cm [∵ PQ = 6 cm]
∵ The perpendicular from the centre of a circle to chord bisects the chord
Exercise 10.6
Page Number 186
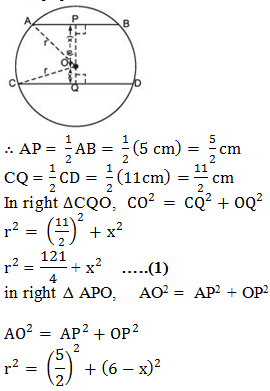
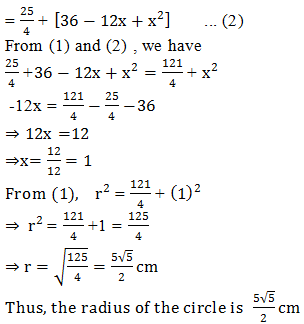
3
The lengths of two parallel chords of a circle are 6 cm and 8 cm. If the smaller chord is at distance 4 cm from the centre, what is the distance of the other chord from the centre?
REMEMBER : The longer chord in a circle is nearer to the centre than the smaller chord.
REMEMBER : The longer chord in a circle is nearer to the centre than the smaller chord.
Answer
We have a circle with centre O. Parallel chords AB and CD are such that the smaller chord is 4 cm away from the centre.Let us draw OP ⊥ AB and join OA and OC.
∴ OP ⊥ AB
∴ P is the mid-point of AB.
Now in right ΔOPA, we have
OA2 = OP2 + AP2
⇒ r2 = 42 + 32
⇒ r2 = 16 + 9 = 25
⇒ r=√25 = 5 cm
Note: r2 = 25
⇒ r = ± 5
But we reject r = -5, because distance cannot be negative.
Again, in right ΔCQO, we have
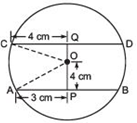
OC2 = OQ2 + CQ2
⇒ r2 = OQ2 + 42
⇒ OQ2 = r2 − 42
⇒ OQ2 = 52 − 42 = 25 − 16 = 9 [∵ r = 5 cm]
⇒ OQ = √9 = 3 cm
The distance of the other chord (CD) from the centre is 3 cm.
Note: In case we take the two parallel chords on either side of the centre, then
In ΔPOA,
OA2 =OP2 + PA2
⇒ r2 =42 + 32 = 52
⇒ r = 5 cm
In ΔQOC,
OC2 =CQ2 + OQ2
⇒ r2 =42 + OQ2
⇒ OQ2 = 52 - 42 = 9
⇒ OQ = 3 cm
Exercise 10.6
Page Number 186
4
Let the vertex of an angle ABC be located outside a circle and let the sides of the angle intersect equal chords AD and CE with the circle. Prove that ∠ABC is equal to half the difference of the angles subtended by the chords AC and DE at the centre.
Answer
We have an ∠ABC such that the arms BA and BC on production, make two equal chords AD and CE. Let us join AC, DE and AE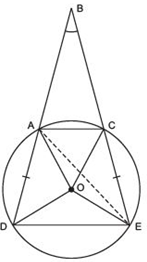
∵ An exterior angle of a triangle is equal to the sum of interior opposite angles.
∴ In ΔBAE, we have Exterior
∠DAE = ∠ABC + ∠AEC …(1)
∵ The chord DE, subtends ∠DOE at the centre and ∠DAE in the remaining part of the circle.
∴ ∠DAE = (1/2)∠DOE …(2)
Similarly,
∠AEC =(1/2)∠AOC …(3)
From (1), (2) and (3), we have
(1/2)∠DOE = ∠ABC + (1/2)∠AOC
⇒ ∠ABC = (1/2)∠DOE - (1/2)∠AOC
⇒ ∠ABC = (1/2) [∠DOE - ∠AOC]
⇒ ∠ABC = (1/2)[(Angle subtended by the chord DE at the centre) - (Angle subtended by the chord AC at the centre)]
⇒ ∠ABC =(1/2) [Difference of the angles subtended by the chords DE and AC]
Exercise 10.6
Page Number 186
5
Prove that the circle drawn with any side of a rhombus as diameter, passes through the point of intersection of its diagonals.
Answer
We have a rhombus ABCD such that its diagonals AC and BD intersect at O.Taking AB as diameter, a circle is drawn. Let us draw PQ || AD and RS || AB, both passing through O. P, Q, R and S are the mid-points of DC, AB, AD and BC respectively. ∵ All the sides of a rhombus are equal.
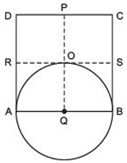
∴ AB = DC
⇒ (1/2) AB =(1/2) DC
⇒ AQ = DP
⇒ BQ = DP
⇒ AQ = BQ [∵ Q is the mid-point of AB] ...(1)
Similarly,
RA = SB
⇒ RA = QO [∵ PQ is drawn parallel to AD] …(2)
From (1) and (2), we have
QA = QB = QO
i.e. A circle drawn with Q as centre, will pass through A, B and O.
Thus, the circle passes through the point of intersection (O) of the diagonals of the rhombus ABCD.
Exercise 10.6
Page Number 186
6
ABCD is a parallelogram. The circle through A, B and C intersect CD (produced if necessary) at E. Prove that AE = AD.
Answer
We have a parallelogram ABCD. A circle passing through A, B and C is drawn such that it intersects CD at E.∵ ABCE is a cyclic quadrilateral.
∴ ∠AEC + ∠B = 180º …(1)
[∵ Opposite angles of a cyclic quadrilateral are supplementary]
But ABCD is a parallelogram. [Given]
∴ ∠D= ∠B …(2)
[∵ Opposite angles of a parallelogram are equal]
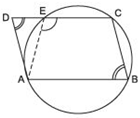
From (1) and (2), we have
∠AEC + ∠D = 180º …(3)
But, ∠AEC + ∠AED = 180º …(4)
From (3) and (4), we have ∠D= ∠AED
i.e. The base angles of ΔADE are equal.
∴ Opposite sides must be equal.
⇒ AD = AE
Exercise 10.6
Page Number 186
7
AC and BD are chords of a circle which bisect each other. Prove that
(i) AC and BD are diameters,
(ii) ABCD is a rectangle.
(i) AC and BD are diameters,
(ii) ABCD is a rectangle.
Answer
We have a circle with centre at O. Two chords AC and BD are such that they bisect each other. Let their point of intersection be O.
Let us join AB, BC, CD and DA.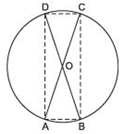
(i) To prove that AC and BD are the diameters of the circle.
In ΔAOB and ΔCOD, we have
AO = OC [∵ O is the mid-point of AC]
BO = DO [∵ O is the mid-point of BD]
∠AOB = ∠COD [Vertically opposite angles]
∴ Using the SAS criterion of congruence,
ΔAOB ≌ ΔCOD
⇒ AB = CD
⇒ arc AB = arc CD ...(1)
Similarly,
arc AD = arc BC ...(2)
Adding (1) and (2),
arc AB + arc AD = arc CD + arc BC
⇒ BD divides the circle into two equal parts.
∴ BD is a diameter.
Similarly, AC is a diameter.
(ii) To prove that ABCD is a rectangle.
We have already proved that, ΔAOB ≌ ΔCOD
⇒ ∠OAB = ∠OCD
⇒ ∠BAC = ∠ABD (c.p.c.t)
⇒ AB || CD
Similarly,
AD || BC
∴ ABCD is a parallelogram.
Since, opposite angles of a parallelogram are equal.
∴ ∠DAB = ∠DCB
But ∠DAB + ∠DCB = 180º [∵ Sum of the opposite angles of a cyclic quadrilateral is 180º]
⇒ ∠DAB = 90º = ∠DCB
Thus, ABCD is a rectangle.
Exercise 10.6
Page Number 186
8
Bisectors of angles, A, B and C of a triangle ABC intersect its circumcircle at D, E and F respectively. Prove that the angles of the triangle DEF are
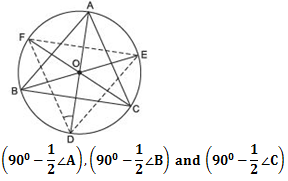
Answer
We have a triangle ABC inscribed in a circle, such that bisectors of ∠A, ∠B and ∠C intersect the circumcircle at D, E and F respectively.Let us join DE, EF and FD.
∵ Angles in the same segment are equal.
∴ ∠FDA = ∠FCA …(1)
∠EDA = ∠EBA …(2)
Adding (1) and (2), we have
∠FDA + ∠EDA = ∠FCA + ∠EBA
Exercise 10.6
Page Number 186
9
Two congruent circles intersect each other at points A and B. Through A any line segment PAQ is drawn so that P, Q lie on the two circles. Prove that BP = BQ.
Answer
We have two congruent circles such that they intersect each other at A and B. A line passing through A, meets the circle at P and Q. Let us draw the common chord AB.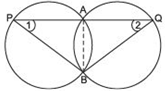
∵ Angles subtended by equal chords in the congruent circles are equal.
∴ ∠APB = ∠AQB
Now, in ΔPBQ, we have
∠1= ∠2 [Proved]
∴ Their opposite sides must be equal.
⇒ PB = BQ
Exercise 10.6
Page Number 187
10
In any triangle ABC, if the angle bisector of ∠ A and perpendicular bisector of BC intersect, prove that they intersect on the circumcircle of the triangle ABC.
Answer
We have a ΔABC inscribed in a circle. The internal bisector of ∠A and the bisector of BC intersect at E.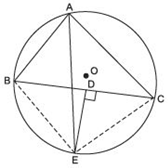
Let us join BE and CE.
∵ ∠BAE = ∠CAE [∵ AE is the bisector of ∠ BAC]
∴ arc BE = arc EC
⇒ chord BE = chord EC
In ΔBDE and ΔCDE, we have
BE = CE
BD = CD [Given]
DE = DE [Common]
∴ By SSS criterion of congruence,
ΔBDE ≌ ΔCDE
⇒ Their corresponding parts are equal.
∴ ∠BDE = ∠CDE
But ∠BDE + ∠CDE = 180º [Linear pairs]
⇒ ∠BDE = ∠CDE = 90º i.DE ⊥ BC
Thus, DE is the perpendicular bisector of BC.
Exercise 10.6
Page Number 187