Areas of Parallelograms and Triangles

Class 9 > Math > NCERT > Areas of Parallelograms and Triangles

NCERT Solutions for Chapter 9 Areas of Parallelograms and triangles Class 9 Maths

Book Solutions

1

Which of the following figures lie on the same base and between the same parallels.
In such a case, write the common base and the two parallels.

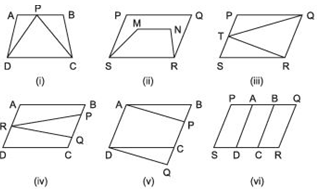
Answer

The figures (i), (iii), and (v) lie on the same base and between the same parallels.

  Common base Two parallels
Fig. (i)
Fig. (iii)
Fig. (v)		 DC
QR
AD		 DC and AB
QR and PS
AD and BQ
Exercise 9.1 Page Number 155

1

In the figure, ABCD is a parallelogram, AE ⊥ DC and CF ⊥ AD. If AB = 16 cm, AE = 8 cm and CF = 10 cm, find AD.

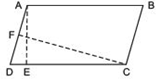
Answer

We have AE ⊥ DC and AB = 16 cm
∵ AB = CD  [opp. sides of parallelogram ABCD]
∴ CD = 16 cm

Now,

area of parallelogram ABCD = CD x AE

= 16 x 8 cm2   [∴ AE = 8 cm (Given)]
= 128 cm2
Since, CF ⊥ AD
∴ Area of parallelogram ABCD = AD x CF
⇒ AD x CF = 128
⇒ AD x 10 = 128  [∵CF = 10 cm]
⇒ AD = (128/10)
= 12.8
Thus, the required length of AD is 12.8 cm.

Exercise 9.2 Page Number 159

2

If E, F, G and H are respectively the mid-points of the sides of a parallelogram ABCD, show that
ar (EFGH) = (1/2) ar (ABCD).

Answer


Let us join E and G
If a D and a parallelogram are on the same base and between the same parallels, then the area of the triangle is equal to half the area of the parallelogram.
∵ E and G are the mid-points of AB and CD respectively.
∴ EG is parallel to BC or AD.
Also,

ar (parallelogram EBCG) = ar (parallelogram AEGD)
= (1/2) ar (parallelogram ABCD)   …(1)
Now, ΔEFG and parallelogram EBCG are on the same base EG, and between the same parallels EG and BC.
∴ ar (ΔEFG) = (1/2) ar (parallelogram EBCG)   …(2)
Similarly, ar (ΔEHG) = (1/2)
ar (parallelogram AEGD)   …(3)
Adding (2) and (3), we get
ar (ΔEFG) + ar (ΔEHG)
= (1/2) [ar (parallelogram EBCG) + ar (parallelogram AEGD)]
⇒ ar (EFGH)
=(1/2) [ (1/2)ar (parallelogram ABCD) + (1/2)ar (parallelogram ABCD)]
[from (1)]
⇒ ar (EFGH) =(1/2) [ar (parallelogram ABCD)]
Thus, ar (EFGH) = (1/2)ar (ABCD).
Note: By joining H and F, we can also have
ar (ΔHEF) + ar (ΔHGF)
= (1/2) [(1/2)ar (parallelogram ABCD) + (1/2)ar (parallelogram ABCD)]
⇒ ar (EFGH) =(1/2) ar (ABCD)

Exercise 9.2 Page Number 159

3

‘P’ and ‘Q’ are any two points lying on the sides DC and AD respectively of a parallelogram ABCD. Show that ar (ΔAPB) = ar(ΔBQC).

Answer

∵ ABCD is a parallelogram.
∴ AB || CD and BC || AD.
Now,

ΔAPB and parallelogram ABCD are on the same base AB and between the same parallels AB and CD.
∴ ar (ΔAPB) =(1/2) ar (parallelogram ABCD)  …(1)
Also,

ΔBQC and parallelogram ABCD are on the same base BC and between the same parallels BC and AD.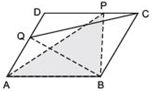

∴ ar (ΔBQC) = (1/2) ar (parallelogram ABCD)  …(2)
From (1) and (2), we have ar (ΔAPB) = ar (ΔBQC).

Exercise 9.2 Page Number 159

4

In the figure, P is a point in the interior of a parallelogram ABCD. Show that

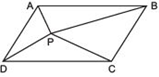
(i) ar (ΔAPB) + ar (ΔPCD) = (1/2) ar (ABCD)
(ii) ar (ΔAPD) + ar (ΔPBC) = ar (ΔAPB) + ar (ΔPCD)
Hint: Through P, draw a line parallel to AB.

Answer

(i) We have a parallelogram ABCD, i.e.

AB || CD and BC || AD.
Let us draw EF || AB, through P.
Since, AB || EF,
∴ ΔAPB and parallelogram AEFB are on the same base AB and between the same parallels AB and EF.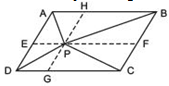

∴ ar (ΔAPB) = (1/2)ar (AEFB)   …(1)
Also, Δ(PCD) and parallelogram CDEF are on the same base CD and between the same parallels CD || EF.
ar (ΔPCD) = (1/2)ar (parallelogram CDEF)   …(2)
Adding (1) and (2), we have

ar (ΔAPB) + ar (ΔPCD)
= (1/2)ar (AEFB) + (1/2)ar (CDEF)
⇒ ar (ΔAPB) + ar (ΔPCD) = (1/2)ar (ABCD)


(ii) Let us join GH || BC, through P.
∴ ΔAPD and parallelogram ADGH are on the same base AD and between the same parallels AD and GH.
∴  ar (ΔAPD) = (1/2) ar (ADGH)  …(3)
Similarly,

ar (ΔPBC) =(1/2) ar (BCGH)  …(4)
Adding (3) and (4), we have

ar (ΔAPD) + ar (ΔPBC)
=(1/2) ar (ADGH) +(1/2) ar (BCGH)
ar (ΔAPD) + ar (ΔPBC) =(1/2) ar (ABCD)   …(5)
But, ar (ΔAPB) + ar (ΔPCD) =(1/2) ar (ABCD)   …(6)
From (5) and (6), we have:

ar (ΔAPD) + ar (ΔPBC) = ar (ΔAPB) + ar (ΔPCD)

Exercise 9.2 Page Number 159

5

In the figure, PQRS and ABRS are parallelograms and X is any point on side BR. Show that
(i) ar (PQRS) = ar (ABRS)

(ii) ar (AXS) =(1/2) ar (PQRS)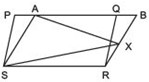

Answer

We have two parallelograms ABRS and PQRS and a point X on BR.

(i) To prove that ar (PQRS) = ar (ABRS)
∵ Parallelogram PQRS and parallelogram ABRS are on the same base RS and between the same parallels RS and PAQB.
∴ ar (PQRS) = ar (ABRS)


(ii) To prove that:

ar (AXS) = (1/2)  ar (PQRS)
∵ ΔAXS and parallelogram ABRS are on the same base AS and between the same parallels AS and BR.
∴ ar (ΔAXS) = (1/2) ar (ABRS)   …(1)
But, ar (parallelogram PQRS) = ar (parallelogram ABRS) (Proved) …(2)
From (1) and (2), we have

ar (ΔAXS) = (1/2) ar (parallelogram PQRS)

Exercise 9.2 Page Number 159

6

A farmer was having a field in the form of a parallelogram PQRS. She took any point ‘A’ on RS and joined it to ‘P’ and ‘Q’. In how many parts the field is divided? What are the shapes of these parts? The farmer wants to sow wheat and pulses in equal portions of the field separately.
How should she do it?

Answer

The farmer is having the field in the form of parallelogram PQRS, and a point A is situated at RS.
Let us join AP and AQ.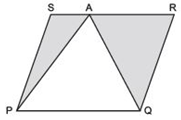

Obviously the field is divided into three parts i.e. in ΔAPS, ΔPAQ and ΔQAR, i.e these parts are triangular in shape.
Since ΔPAQ and parallelogram PQRS are on the same base and between the same parallels PQ and RS.
∴ ar (ΔPAQ) =(1/2) ar (parallelogram PQRS)    …(1)
⇒ ar (parallelogram PQRS) - ar (ΔPAQ) = ar (parallelogram PQRS) - (1/2) ar (parallelogram PQRS)
⇒ [ar (ΔAPS) + ar (ΔQAR)] = (1/2) ar (parallelogram PQRS)    …(2)
From (1) and (2), we have

ar (ΔPAQ) = ar [(ΔAPS) + (ΔQAR)]
Thus, the farmer can sow wheat in (ΔPAQ) and pulses in [(ΔAPS) + (ΔQAR)] OR

wheat in [(ΔAPS) + (ΔQAR)] and pulses in (ΔPAQ).

Exercise 9.2 Page Number 160

1

In the figure, E is any point on median AD of a DABC.
Show that ar (ABE) = ar (ACE).

Answer

We have a ΔABC such that AD is a median. ∴
ar (ΔABD) = ar (ΔADC)   ...(1)
[∵ A median divides the triangle into two triangles of equal areas.]
Similarly, in DBEC, we have

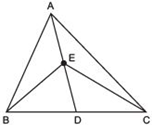
ar (ΔBED) = ar (ΔDEC)  …(2)
Subtracting (2) from (1), we have
ar (ΔABD) - ar (ΔBED) = ar (ΔADC) - ar (ΔDEC)
⇒ ar (ΔABE) = ar (ΔACE).
Exercise 9.3 Page Number 162

2

In a triangle ABC, E is the mid-point of median AD.
Show that ar (BED) =  ar (ABC).

Answer

We have a ΔABC and its median AD.
Since, a median divides the triangle into two triangles equal in area.
∴ ar (ΔABD) = (1/2) ar (ΔABC)  …(1)

Let us join B and E.
Now, in ΔABD, BE is a median. [∵ E is the mid-point of AD]
∴ ar (ΔBED) = (1/2)ar (ΔABD)
From (1) and (2), we have

ar (ΔBED) = (1/2)[(1/2)]ar ( ABC) ]
⇒ ar (ΔBED) = (1/4)ar (ΔABC)

Exercise 9.3 Page Number 162

3

Show that the diagonals of a parallelogram divide it into four triangles of equal area.

Answer

We have a parallelogram ABCD such that its diagonals intersect at O.
∵ Diagonals of a parallelogram bisect each other.
∴ AO = OC and BO = OD Let us draw CE ⊥ BD.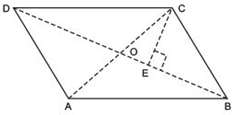

Now, ar (ΔBOC) = (1/2) BO x CE
and ar (ΔDOC) = (1/2) OD x CE
Since, BO = OD
ar (ΔBOC) = ar (ΔDOC)   …(1)
Similarly,

ar (ΔAOD) = ar (ΔDOC)   …(2)
and ar (ΔAOB) = ar (BOC)   …(3)
From (1), (2) and (3), we have
ar (ΔAOB) = ar (ΔBOC) = ar (ΔBOC) = ar (ΔAOD)

Thus, the diagonals of a parallelogram divide it into four triangles of equal area.

Exercise 9.3 Page Number 162

4

In figure, ABC and ABD are two triangles on the same base AB. If line segment CD is bisected by AB at O, show that ar (ABC) = ar (ABD).

Answer

We have ΔABC and ΔABD are on the same base AB.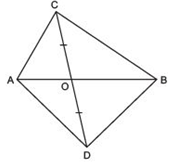

∵ CD is bisected at O  [Given]
∴ AO = BO
Now, in ΔACD, AO is a median.
∴  ar (ΔOAC) = ar (ΔOAD)  …(1)
Again, in DBCD, BO is a median.
∴  ar (ΔOBC) = ar (ΔODC)   …(2)
Adding (1) and (2), we have

ar (ΔOAC) + ar (ΔOBC) = ar (ΔOAD) + ar (ΔODC)
⇒ ar (ΔABC) = ar (ΔABD)

Exercise 9.3 Page Number 162

5

D, E and F are respectively the mid-points of the sides BC, CA and AB of a ΔABC. Show that:
(i) BDEF is a parallelogram.
(ii) ar (DEF) = (1/4) ar (ABC)
(iii) ar (BDEF) = (1/2)ar (ABC)

Answer

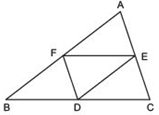
We have: ΔABC such that the mid-points of BC, CA and AB are respectively D, E and F.
(i) To prove that BDEF is a parallelogram.
In ΔABC, E and F are the mid-points of AC and AB.
∴ EF || BC
⇒ EF || BD
Also,

EF =(1/2) BC
⇒ EF = BD   [∵ D is the mid-point of BC.]
∵ BDEF is a quadrilateral whose one pair of opposite sides is parallel and of equal lengths.
∴ BDEF is a parallelogram.


(ii) To prove that ar (DEF) = (1/4)ar (ABC).
We have proved that BDEF is a parallelogram.
Similarly,

CDEF is a parallelogram and ΔEAF is a parallelogram.
Now, parallelogram BDEF and parallelogram CDEF are on the same base EF and between the same parallels BC and EF.
∴ ar (BDEF) = ar (CDEF)
⇒(1/2) ar (BDEF) = (1/2)ar (DEF)
⇒ ar (ΔBDF) = ar (ΔCDF) …(1)
[∵ Diagonal of a parallelogram divides it into two triangles of equal area]
Similarly,

ar (ΔCDE) = ar (ΔDEF)  …(2)
ar (ΔAEF) = ar (ΔDEF)  …(3)
From (1), (2) and (3), we have
ar (ΔAEF) = ar (ΔFBD) = ar (ΔDEF) = ar (ΔCDE)
Thus,

ar (ΔABC) = ar (ΔAEF) + ar (ΔFBD) + ar (ΔDEF) + ar (ΔCDE)
= 4 ar (ΔDEF)
⇒ ar (ΔDEF) = (1/4) ar (ΔABC)


(iii) To prove that ar (BDEF) = (1/2)ar (ABC).
We have ar (BDEF) = ar (ΔBDF) + ar (ΔDEF)
= ar (ΔDEF) + ar (ΔDEF)   [∵ ar (ΔDEF) = ar (ΔBDF)]
= 2 ar(ΔDEF)
= 2 [(1/4)ar ( ABC)]
= 2 x (1/4)ar (ΔABC)
= (1/2)ar (ΔABC)
Thus, ar (BDEF) =(1/2)ar (ΔABC)

Exercise 9.3 Page Number 163

6

In the figure, diagonals AC and BD of a quadrilateral ABCD intersect at O such that OB = OD. If AB = CD, then show that

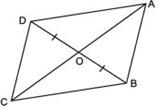
(i) ar (DOC) = ar (AOB)
(ii) ar (DCB) = ar (ACB)
(iii) DA || CB or ABCD is a parallelogram.
Hint: From D and B, draw perpendiculars to AC.

Answer

We have a quadrilateral ABCD whose diagonals AC and BD intersect at O. We also have that OB = OD
AB = CD
Let us draw DE ⊥ AC and BF ⊥ AC


(i) To prove that ar (ΔDOC) = ar (ΔAOB)
In ΔDEO and ΔBFO, we have
DO = BO   [Given]
∠DOE = ∠BOF  [Vertically opposite angles]
∠DEO = ∠BFO  [Each = 90º]
∴ ΔDEO ≌ ΔBFO   [ASA criteria]
⇒ DE = BF   [c.p.c.t]
and ar (ΔDEO) = ar (ΔBFO) …(1)
[∵ Congruent triangle are equal in areas]
Now, in ΔDEC and ΔBFA, we have
∠DEC = ∠BFA [Each = 90º]
DE = BF [Proved]
DC = BA [Given]
∴ ΔDEC ≌ ΔBFA  [RHS criteria]
⇒ ar (ΔDEC) = ar (ΔBFA)  …(2)
Adding (1) and (2), we have

ar (ΔDEO) + ar (ΔDEC) = ar (ΔBFO) + ar (ΔBFA)
⇒ ar (ΔDOC) = ar (ΔAOB)

 

(ii) To prove that ar (DCB) = ar (ACB)
∵ ar (ΔDOC) = ar (ΔAOB)   [Proved]
∴ Adding ar (ΔBOC), on both sides, we have
ar (ΔDOC) + ar (ΔBOC) = ar (ΔAOB) + ar (ΔBOC)
⇒ ar (ΔDCB) = ar (DACB)


(iii) To prove that DA || CB
∵ ΔDCB and ΔACB are on the same base CB and having equal areas.
∴ They lie between the same parallels CB and DA.
⇒ CB || DA (or ABCD is a parallelogram)

Exercise 9.3 Page Number 163

7

D and E are points on sides AB and AC respectively of ΔABC such that ar (DBC) = ar (EBC). Prove that DE || BC.

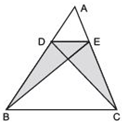
Answer

We have ΔABC and points D and E are such that ar (DBC) = ar (EBC)

Since, ΔDBC and ΔEBC are on the same base DE and having same area.
∴ They lie between the same parallels DE and BC. ⇒ DE || BC.

Exercise 9.3 Page Number 163

8

XY is a line parallel to side BC of a triangle ABC. If BE || AC and CF || AB meet XY at E and F respectively, show that ar (ABE) = ar (ACF).

Answer

We have a ΔABC such that  XY || BC, BE || AC and CF || AB.
Since,

XY || BC and BE || CY
∴ BCYE is a parallelogram.
Now, the parallelogram BCYE and ΔABE are on the same base BE and between the same parallels BE and AC.
∴ ar (ΔABE) = (1/2)ar (BCYE)   …(1)
Again,

CF || AB   [Given]
XY || BC   [Given]
⇒ CF || AB and XF || BC
∴ BCFX is a parallelogram.
Now, ΔACF and parallelogram BCFX are on the same base CF and between the same parallels AB and FC.
∴ ar (ΔACF) = (1/2)ar (BCFX)  …(2)
Also parallelogram BCFX and parallelogram BCYE are on the same base BC and between the same parallels.
∴ ar (BCFX) = ar (BCYE)   ....(3)
From (1), (2) and (3) we get
ar (ΔABE) = ar(ΔACF)

Exercise 9.3 Page Number 163

9

The side AB of a parallelogram, ABCD is produced to any point P. A line through A and parallel to CP meets CB produced at Q and then parallelogram PBQR is completed (see figure). Show that ar (ABCD) = ar (PBQR).
Hint: Join AC and PQ. Now compare ar (ACQ) and ar (APQ).

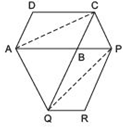
Answer

We have a parallelogram ABCD. AB is produced to P. CB is produced to Q and PBQR is completed.
Let us join AC and PQ.
∵ ABCD is a parallelogram [Given] and AC is its diagonal.
ar (ΔABC) = (1/2)ar (parallelogram ABCD)   …(1)
∵ BQRP is a parallelogram [Given] and QP is its diagonal.
∴   ar (ΔBPQ) = (1/2)ar (parallelogram BQRP)   …(2)
Since ΔACQ and ΔAPQ are on the same base AQ and between the same parallels AQ and CP.
∴  ar (ΔACQ) = ar (ΔAPQ)  [∵ Triangles on the same base and between the same parallels are equal.]
⇒ ar (ΔACQ)  - ar (ΔABQ) = ar (DAPQ) - ar (DABQ)  [Subtracting ar (ΔABQ) from both sides]
⇒ ar (ΔABC) = ar (ΔBPQ)   …(3)
From (1), (2) and (3), we get

(1/2)ar (parallelogram ABCD) = (1/2)ar (parallelogram BQRP)
⇒ 2 [(1/2)ar (parallelogram ABCD)] = 2 [(1/2)ar (parallelogram BQRP)]
⇒ ar (parallelogram ABCD) = ar (parallelogram BQRP)

Exercise 9.3 Page Number 163

10

Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at O. Prove that ar (AOD) = ar (BOC).

Answer

We have a trapezium ABCD having AB || CD and its diagonals AD and BC are joined.
Since, triangles on the same base and between the same parallels have equal areas.

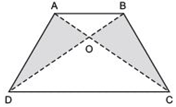
∵ ΔABD and ΔABC are on the same base AB and between the same parallels AB and DC.
∴ ar (ΔABD) = ar (ΔABC)
Subtracting ar (ΔAOB) from both sides, we get
[ar (ΔABD) – ar (ΔAOB)] = [ar (ΔABC) – ar (ΔAOB)]
⇒ ar (ΔAOD) = ar (ΔBOC)
Exercise 9.3 Page Number 163

11

In the figure, ABCDE is a pentagon. A line through B parallel to AC meets DC produced at F. Show that
(i) ar (ACB) = ar (ACF)
(ii) ar (AEDF) = ar (ABCDE)

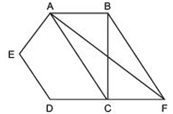
Answer

We have a pentagon ABCDE in which BF || AC and DC is produced to F.


(i) To prove ar (ΔACB) = ar (ΔACF)
Since, the triangles between the same parallels and on the same base are equal in area.
∵ ΔACB and ΔACF are on the same base AC and between AC and BF.
∴ ar (ΔACB) = ar (ΔACF)


(ii) Since, ar (ΔACB) = ar (ΔACF) [Proved]

Adding ar (AEDC) to both sides, we get
⇒ [ar (ΔACB) + ar (AEDC)] = [ar (ΔACF) + ar (AEDC)]
⇒ ar (AEDF) = ar (ABCDE)

Exercise 9.3 Page Number 163

12

A villager Itwaari has a plot of land of the shape of a quadrilateral. The Gram Panchayat of the village decided to take over some portion of his plot from one of the corners to construct a Health Centre. Itwaari agrees to the above proposal with the condition that he should be given equal amount of land in lieu of his land adjoining his plot so as to form a triangular plot.
Explain how this proposal will be implemented.

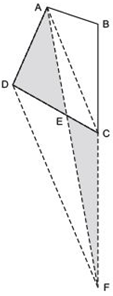
Answer

We have a plot in the form of a quadrilateral ABCD.
Let us draw DF || AC and join A and F.
Now, ΔDAF and ΔDCF are on the same base DF and between the same parallels AC and DF.
∴  ar (ΔDAF) = ar (ΔDCF)

Subtracting ar(ΔDEF) from both sides, we get
[ar (ΔDAF) - ar (ΔDEF)] = [ar (ΔDCF) - ar (ΔDEF)]
⇒ ar (ΔADE) = ar (ΔCEF)
The portion ΔADE can be taken over by the Gram Panchayat by adding the land (ΔCEF) to his (Itwaari) land so as to form a triangular plot, i.e. ΔABF.
Let us prove that,

ar (ΔABF) = ar (quadrilateral ABCD), we have
ar (ΔCEF) = ar (ΔADE) [Proved]

Adding ar (ABCE) to both sides, we get
[ar (ΔCEF) + ar (ABCE)] = [ar (ΔADE) + ar (ABCE)]
⇒ ar (ΔABF) = ar (quadrilateral ABCD)

Exercise 9.3 Page Number 164

13

ABCD is a trapezium with AB || DC. A line parallel to AC intersects AB at X and BC at Y. Prove that ar (ADX) = ar (ACY).

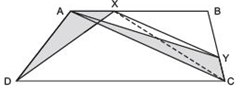
Hint: Join CX.

Answer

We have a trapezium ABCD such that AB || DC.
XY || AC meets AB at X and BC at Y.

Let us join CX.
∵ AB || DC [Given]
∴ ΔADX and ΔACX are on the same base AX and between the same parallels AB and DC.
∴  ar (ΔADX) = ar (ΔACX)  …(1)
∵ AC || XY  [Given]
∴ ΔACX and ΔACY are on the same base AC and between the same parallels AC and XY.
∴  ar (ΔACX) = ar (ΔACY)   …(2)
From (1) and (2), we have
ar (ΔADX) = ar (ΔACY).
Exercise 9.3 Page Number 164

14

In the figure, AP || BQ || CR. Prove that ar (AQC) = ar (PBR).

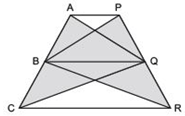
Answer

We have AP || BQ || CR
Since, BQ || CR [Given]
∴ ΔBCQ and ΔBQR are on the same base BQ and between the same parallels BQ and CR.

⇒ ar (ΔBCQ) = ar (ΔBQR)   …(1)
Again, AP || BQ  [Given]
∵ ΔABQ and ΔPBQ are on the same base BQ and between the same parallels.
∴ ar (ΔABQ) = ar (ΔPBQ)   …(2)
Adding (1) and (2), we have
[ar (ΔBCQ) + ar (ΔABQ)] = [ar (ΔBQR) + ar (ΔPBQ)]
⇒ ar (ΔAQC) = ar (ΔPBR)
Exercise 9.3 Page Number 164

15

Diagonals AC and BD of a quadrilateral ABCD intersect at O in such a way that ar (AOD) = ar (BOC). Prove that ABCD is a trapezium.

Answer

We have a quadrilateral ABCD and its diagonals AC and BD intersect at O such that ar (ΔAOD) = ar (ΔBOC).
Now, ar (ΔAOD) = ar (ΔBOC)  [Given]
Adding ar (ΔAOB) to both sides, we have
[ar (AOD) + ar (AOB)] = [ar (BOC) + ar (AOB)]
⇒ ar (ΔABD) = ar (ΔABC)

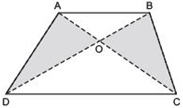
But they are on the same base AB.
Since, the triangles on the same base and having equal area lie between the same parallels.
∴ AB || DC
Now, ABCD is a quadrilateral having a pair of opposite sides parallel.
∴ ABCD is a trapezium.
Exercise 9.3 Page Number 164

16

In the figure, ar (DRC) = ar (DPC) and ar (BDP) = ar (ARC). Show that both the quadrilaterals ABCD and DCPR are trapeziums.

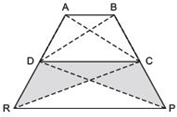
Answer

We have ar (ΔDRC) = ar (ΔDPC)

[Given] But they are on the same base DC.
∴ ΔDRC and ΔDPC must lie between the same parallels.
⇒ DC || RP
⇒ One pair of opposite sides of quadrilateral DCPR is parallel.
∴ Quadrilateral DCPR is a trapezium.
Again, we have

ar Δ(BDP) = ar Δ(ARC) [Given] .…(1)
Also,

ar (ΔDPC) = ar Δ(DRC) [Given]  ….(2)
Subtracting (2) from (1), we get,

[ar (ΔBDP) - ar (ΔDPC)] = [ar (ΔARC) - ar (ΔDRC)]
⇒ ar (ΔBDC) = ar (ΔADC)

But they are on the same base DC.
∴ ΔBDC and ΔADC must lie between the same parallels.
⇒ AB || DC i.e. A pair of quadrilateral ABCD is parallel
∴ Quadrilateral ABCD is a trapezium.

Exercise 9.3 Page Number 164

1

Parallelogram ABCD and rectangle ABEF are on the same base AB have equal areas. Show that the perimeter of the parallelogram is greater than that of the rectangle.

Answer

We have a parallelogram ABCD and rectangle ABEF such that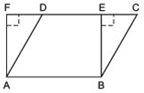

ar (parallelogram ABCD) = ar (rectangle ABEF)
∵ AB = CD   [∵ Opposite sides of a parallelogram are equal]
and AB = EF  [∵ Opposite sides of a rectangle are equal]
⇒ CD = EF ⇒ AB + CD = AB + EF  …(1)
∵ BE < BC
and AF < AD   [∵ In a right triangle, hypotenuse is the longest side.]
∴ BC > BE and AD > AF

⇒ (BC + AD) > (BE + AF)   …(2)
Adding (1) and (2), we have
(AB + CD) + (BC + AD) > (AB + EF) + (BE + AF)
⇒ (AB + BC + CD + DA) > (AB + BE + EF + FA)
⇒ [Perimeter of parallelogram ABCD] > [Perimeter of rectangle ABEF]

Exercise 9.4 Page Number 164

2

In the figure, D and E are two points on BC such that BD = DE = EC. Show that ar (ABD) = ar (ADE) = ar (AEC) Can you now, answer the question that you have left in the ‘Introduction’ of this chapter, whether the field of Budhia has been actually divided into three parts of equal area?

Remark: Note that by taking BD = DE = EC, the triangle ABC is divided into three triangles ABD, ADE and AEC of equal areas. In the same way, by dividing BC into n equal parts and joining the points of division so obtained to the opposite vertex of BC, you can divide ΔABC into n triangles of equal areas.

Answer

Let us draw AF, perpendicular to BC such that AF is the height of ΔABD, ΔADE and ΔAEC.

⇒ ar (ΔABD) = ar (ΔADE) = ar (ΔAEC)
Yes, the altitudes (heights) of all the triangles are same. Therefore, Budhia can use the above result in dividing her land in three equal parts.
Exercise 9.4 Page Number 164

3

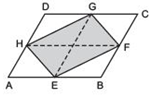
In the figure, ABCD, DCFE and ABFE are parallelograms. Show that ar(ADE) = ar (BCF).

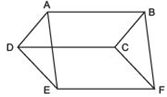
Answer

We have parallelograms ABCD, DCFE and ABFE.

∵ ABCD is a parallelogram [given]

∴ Its opposite sides are parallel and equal.

⇒ AD = BC   …(1)
and AB || DC  …(2)
Since,

DCFE is a parallelogram   [Given]
∴ DC || EF   …(3)
From (2) and (3), we have

AB || EF
Now,

ΔADE and ΔBCF are on equal bases, i.e. AD = BC [from (1)] and between the same parallels,
i.e. AB || EF
∴ ar (ΔADE) = ar (ΔBCF)

Exercise 9.4 Page Number 165

4

In the figure ABCD is a parallelogram and BC is produced to a point Q such that AD = CQ. If AQ intersect DC at P, show that ar (BPC) = ar (DPQ).

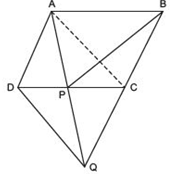
Hint: Join AC.

Answer

We have a parallelogram ABCD and AD = CQ.
Let us join AC. We know that triangles on the same base and between the same parallels are equal in area.

Since,

ΔQAC and ΔQDC are on the same base QC and between the same parallels AD and BQ.
∴ ar (ΔQAC) = ar (ΔQDC)

Subtracting ar (ΔQPC) from both sides, we have
ar (ΔQAC) - ar (ΔQPC) = ar (ΔQDC) - ar (ΔQPC)

⇒ ar (ΔPAC) = ar (ΔQDP)   ...(1)
Since,

ΔPAC ad ΔPBC are on the same base PC and between the same parallels AB and CD.
∴ ar (ΔPAC) = ar (ΔPBC)   …(2)
From (1) and (2), we get

ar (ΔPBC) = ar (ΔQDP)
i.e. ar (ΔPBC) = ar (ΔDPQ)

Exercise 9.4 Page Number 165

5

In Fig.9.33, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that
(i) ar(BDE) = 1/4 ar(ABC)
(ii) ar(BDE) = 1/2 ar(BAE)
(iii) ar (ABC) = 2 ar (BEC)
(iv) ar (BFE) = ar (AFD)
(v) ar (BFE) = 2 ar (FED)
(vi) ar (FED) = 1/8 ar (AFC)
[Hint : Join EC and AD. Show that BE || AC and DE || AB, etc.]

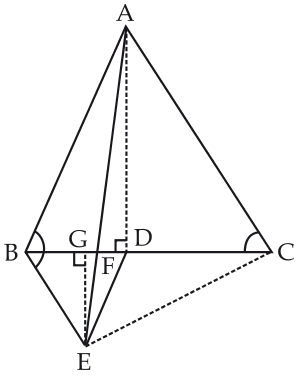
Answer

Join EC and AD.

ΔABC is an equilateral triangle.

∴ ∠BAC = ∠ABC = ∠ACB = 60°

ΔBDE is also an equilateral triangle.

∴ ∠EBD = ∠BED = ∠BDE = 60°

Now if we take two lines,

AC and BE and BC as a transversal.

Then,  ∠EBD = ∠ACB (Each angle 60°)

BE II AC

[∵ When alternate angles are equal then lines are parallel.]

Similarly, for lines AB and DE and BF as transversal.

∠ABC = ∠BDE (Each = 60°) [Alternate angles]

∴ AB II DE

Exercise 9.4 Page Number 165

6

Diagonals AC and BD of a quadrilateral ABCD intersect each other at P. Show that ar (APB) x ar (CPD) = ar (APD) x ar (BPC).
Hint: From A and C, draw perpendiculars to BD.

Answer

We have a quadrilateral ABCD such that its diagonals AC and BD intersect at P.
Let us draw AM ⊥ BD and CN ⊥ BD.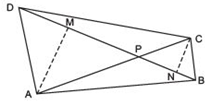


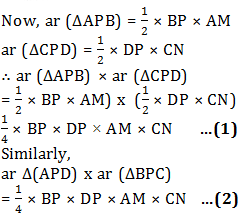
From (1) and (2), we get

ar (ΔAPB) x ar (ΔCPD) = ar (ΔAPD) x ar (ΔBPC).

Exercise 9.4 Page Number 166

7

P and Q are respectively the mid-points of sides AB and BC of a triangle ABC and R is the mid-point of AP, show that

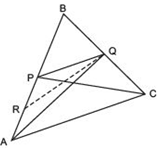
(i) ar(∆PRQ) = (1/2) ar(∆ARC)
(ii) ar(∆RQC) = (3/8) ar(∆ABC)
(iii) ar(∆PBQ) = ar(∆ARC)

Answer

We have a DABC such that ‘P’ is the mid-point of AB and ‘Q’ is the mid-point of BC. Also, ‘R’ is the mid-point of AP. Let us join AQ and PC.

In ΔAPQ, R is the mid-point of AP.   [Given]
Let us join RQ.
∵ RQ is a median of ΔAPQ.



Exercise 9.4 Page Number 166

8

In the figure, ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segment AX ⊥ DE meets BC at Y. Show that:
(i) ΔMBC ≌ ΔABD
(ii) ar (BYXD) = 2ar (∆MBC)
(iii) ar (BYXD) = ar (ABMN)
(iv) ΔFCB ≌ ΔACE
(v) ar(CYXE) = 2 ar(∆FCB)
(vi) ar(CYXE) = ar(ACFG)
(vii) ar(BCED) = ar(ABMN) + ar(ACFG)
Note:  Result (vii) is the famous Theorem of Pythagoras. You shall learn a simpler proof of this theorem in Class X.

Answer

We have a right DABC such that BCED, ACFG and ABMN are squares on its sides BC, CA and AB respectively.
Line segment AX ⊥ DE is also drawn such that it meets BC in Y.


(i) To prove that ΔMBC ≌ ΔABD In DABD and DMBC, we have

AB = MB

BD = BC
[Sides of a square]
∠CBD = ∠MBA   [Each = 90º]
∴ ∠CBD + ∠ABC = ∠MBA + ∠ ABC
or ∠MBC = ∠ABD
∴ ΔMBC ≌ ΔABD


(ii) To prove that: ar (BYXD) = 2 ar (∆ MBC)
Since parallelogram BYXD and DABD are on the same base BD and between the same parallels BD and AX.
∴ ar (ΔABD) = (1/2) ar (parallelogram BYXD)
But ar (ΔABD) = ar (ΔMBC)  [∵Congruent triangles have equal areas]
⇒ ar (ΔMBC) = (1/2) ar (parallelogram BYXD)
or, 2ar (ΔMBC) = ar (BYXD)

Thus, ar (BYXD) = 2ar (ΔMBC)


(iii) To prove that ar (BYXD) = ar (ABMN)
∵ ar (BYXD) = 2ar (ΔMBC)   [from (ii)]  …(1)
and ar(ABMN) = 2 ar(MBC)    ...(2)

[∵ ABMN and DMBC are on the same base MB and between the same parallels MB and NC]
∴ From (1)  and (2), we have

ar (BYXD) = ar (ABMN)


(iv) ΔFCB ≌ ΔACE
In ΔFCB and ΔACE,

FC = AC  [Sides of a square]
CB = CE  [Sides of a square]
∠FCA = ∠BCE
or ∠FCA + ∠ACB = ∠BCE + ∠ACB
⇒∠FCB = ∠ACE
⇒ΔFCB ≌ ΔACE  [SAS rule]
(v) To prove that ar (CYXE) = 2ar (FCB)
Since (CYXE) and (ΔACE) are on the same base CE and between the same parallels CE and AX.
∴ ar (CYXE) = 2ar (ΔACE)
But ΔACE ≌ ΔFCB
Since, congruent triangles are equal in areas.
∴ ar (CYXE) = 2ar(ΔFCB)


(vi) To prove ar(CYXE) = ar (ACFG)
Since, ar (CYXE) = 2ar (ΔFCB)  [from (v)]  ...(3)
Also, (ACFG) and ΔFCB are on the same base FC and between the same parallels FC and BG.
⇒ ar (ACFG) = 2ar (ΔFCB)  …(4)
From (3) and (4), we get

ar (CYXE) = ar (ACFG)   …(5)


(vii ) To prove that ar (BCED) = ar (ABMN) + ar (ACFG)
We have

ar (BCED) = ar (CYXE) + ar (BYXD) = ar (CYXE) + ar (ABMN)  [from (iii)]
Now,

ar (BCED) = ar (ABMN) + ar (CYXE).
Thus, ar (BCED) = ar (ABMN) + ar (ACFG)   [from (5)

Exercise 9.4 Page Number 166

Ads